九年级上综合题（1）
姓名________ 座号______ 得分____
一． 选择题 （每题3分，共30分）请把选择题的答案写在下面的表格里
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | | | | | | | | | | |
1、Rt△ABC中，∠C=900锐角为30o，最短边长为5cm，则最长边上的中线是（ ）
A、5cm B、15cm C、10cm D、2.5cm
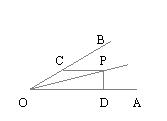
2、如图∠AOP=∠BOP=15o，PC∥OA，PD⊥OA，若PC=4，
则PD等于……（ ）
A、4 B、3 C、2 D、1
3、在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的是（ ） A、AC = BD，AB∥CD，AB = CD B、AD∥BC∠A =∠ C C 、AO=BO=CO=DO，AC⊥BD D 、 AO=CO，BO=DO，AB=BC
4、到△ABC的三个顶点距离相等的点是△ABC的（ ）
A.三边中线的交点
B.三条角平分线的交点
C.三边上高的交点 D.三边垂直平分线的交点
5、如图，⊿ABC中，∠ACB =
，BE平分∠ABC，DE⊥AB，
垂足为D，如果AC = 12
，AD=8cm，那么△ADE的周长为（ ）
A 22
B 17 C 20 D 18
6、某厂今年3月的产值为50万元，5月份上升到72万元，这两个月平均每月增长的百分率是多少？若设平均每月增长的百分率为x，则列出的方程正确的是（ ）
A、50（1+x）＝72 B、50（1+x）＋50（1+x）2＝72
C、50（1+x）×2＝72 D、50（1+x）2＝72
7、如果反比例函数y＝
的图象经过点（2，－3），那么k的值为（ ）
A、－6
B、6
C、－
D、
8、有两个角相等的梯形是（ ）
A、等腰梯形 B、直角梯形 C、一般梯形 D、等腰梯形或直角梯形
9、物体在太阳光的照射下，不同的时刻会发生的现象是（ ）
A、影子的大小不变，方向在变 B、影子的大小在变，方向不变
C、影子的大小在变，方向也在变 D、影子的大小、方向都不变
10、如果反比例函数y＝
（m为常数），当x<0时，y随x的增大而增大，那么m的
取值范围是（ ）
A、m<0
B、m<
C、m>
D、m≥
二、填空题（每题3分，共15分）
11、菱形的一条对角线长是6cm，周长是20cm，则菱形的面积是 cm2。
12、等边三角形的周长是12，则其高是 。
13、已知反比例函数y＝
的图象在第一、三象限内，则m的取值范围是 。
14、甲同学的身高为1.75m，甲、乙两同学在同一时刻受太阳光的照射形成的影子分别为2m和1.8m，则乙同学的身高约为 （精确到0.01m）
15、方程（m－2）x
＋x－4＝0是一元二次方程，则m的值为 。
三解答题（每题6分，共30分）
16、解方程：5x2－5x－1＝0 17、已知：△ABC，在BC边上求一点P，
使它到AB、AC的距离相等
（不写作法，保留作图痕迹）
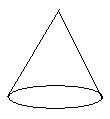
18、已知某圆锥体如图所示，请你画出它的三种视图。
19、反比例函数y＝的图象经过点（32，3），
（1）求它的表达式。（2）求当x＝3时的函数值。
（3）点（2，23）是否在该反比例函数的图象上？为什么？
20、某小区规划在一个长10m，宽8m的矩形场地ABCD上修建三条同样宽的道路，使其中两条与AB平行，另一条与AD平行，如图，其余部分种草，若每块种草面积达到6m2，求道路的宽。
四：证明题：（共24分）
21、已知： ABCD的对角线AC、BD相交于点O，过点O的直线与AD、BC分别相交于点E、F.
求证：OE=OF （8分）
22、已知：在 ABCD中，BF＝DE。求证：四边形AFCE是平行四边形。（8分）
23、如图：DE是△ABC的中位线，∠ABC的平分线交DE于点F.
求证：AF⊥BF (8分)
五：综合题：（共31分）
24、某种服装，平均每天可销售20件，每件盈利44元，若每件降低1元，则每天可多售5件，如果每天要盈利1600元，每件应降价多少元？（8分）
25、如图，是一口呈四边形的池塘，在它四个角A、B、C、D处各种一个大核桃树，现在想使池塘的面积 大一倍，又想保持核桃树不动，并要求 建后的池塘成平行四边形，你能实现这愿望吗？若能，请你设计并画出图形；若不能，请说明理由。（6分）
26、某蓄水池的排水管每时排水8m3，6h可将满池水全部排空。
（1） 蓄水池的容积是多少？（1分）
（2） 如果增加排水管，使每时的排水量达到Q（m3），那么将满池水排空所需的时间的t（h）将如何变化？（1分）
（3） 写出t与Q之间的关系式；（2分）
（4） 如果准备在5h内将满池水排空，那么每时的排水量至少为多少？（2分）
（5） 已知排水管的最大排水量为每时12m3，那么最少多长时间可将满池水全部排空？（2分）
27、如图，在△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA外角平分线于点F.
(1) 求证：EO=FO （4分）
(2) 当点O运动到何处时，四边形AECF是矩形？并证明你的结论。 （5分）
一．