九年级数学单元测试（二）

九年级数学单元测试（二）

（二次函数）

班别　　 　姓名　　　  学号　　 　成 绩　　　

一、填空（每小题3分，共33分）

1、当x＝____时，函数是二次函数．

2、抛物线经过点（3，5），则 = 　　　 ；

3、二次函数的图象过点（0，5），则这个是二次函数为　　　　  ；

4、将抛物线向右平移2个单位后将得到抛物线　　　　　　 ，再向下平移5个单位后将得到抛物线_______　　　　__，此时顶点坐标为____　 ___。

5、抛物线可由抛物线向 　　平移　　　个单位得到。

6、抛物线图象的开口向　_、对称轴是　　_、顶点坐标是　　　。

7、把化为y=的形式，得到　　　　　 ，这个二次函数的图象开口向　　 ，顶点坐标是　　　　，对称轴是直线　　　　　　　 。

8、已知抛物线，则图象的开口向　　　　 ，对称轴是直线　　　　，顶点坐标为　　　　  ；图象与轴的交点坐标为　　　　　 ，与轴的交点坐标为　　　　  。

9、顶点为（－2，－5）且过点（1，－14）的抛物线的解析式为　　　　　　　　  。

10、抛物线，若其顶点在x轴上，则　　　　。

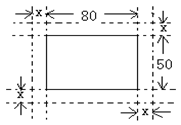11、如图：在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂画，设整个挂画总面积为ycm²，金色纸边的宽xcm，则y与x的关系式是___________________。

二、选择（每小题4分，共40分）

1、下列函数中，图象一定经过原点的函数是　　 （　　）

A. 　　 B.　　C.　　  D.

2、下列函数中，是二次函数是　　 （　　）

A、　　 B、　 C、　　D、

3．把二次函数配方成顶点式为（　　）

A、　 B、　 C、　 D、

4、抛物线的顶点坐标为 （　　 ）

A、（3，4） 　 B、（－3，－4）　　C、（－3，－4）　 D、（－3，4）

5、抛物线的图象（　　 ）

A、开口向上，且有最高点　　 B、开口向上，且有最低点

C、开口向下，且有最高点　　 D、开口向下，且有最低点

6、二次函数的最小值为（　　 ）

A、－1　　　B、－2　　　 C、2　　　D、3

0

－1

0

x

1

x

0

x

0

y

y

y

y

7、函数的图象大致为　 （　　 ）

x

			－1

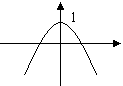A　　　　　　　 B　　　　　　　 C　　　　　　  D

8、函数的图象与轴有交点，则的取值范围是（　　）

A． 　　　B．　　C．　　  D．

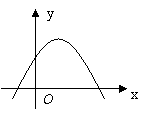9、二次函数的图象如图所示，则下列结论中正确的是：（　 ）

　A  a>0　b<0  c>0　　 B  a<0　b<0　c>0

　C  a<0　b>0　c<0　　 D　a<0　b>0　c>0

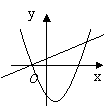
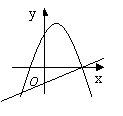
10、已知一次函数与二次函数（），它们在同一坐标系中的大致图象是（　　 ）

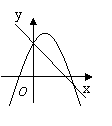A　　　　　 　　 B　　　　　　　  C　　　　　　　 D

三、解答题（共27分）

1、（6分）竖直向上发射物体的h(m)满足关系式y=-5t²+v₀t，其中t(s)是物体运动的时间，v₀(m/s)是物体被发射时的速度.某公园计划设计园内喷泉，喷水的最大高度要求达到15m,那么喷水的速度应该达到多少？(结果精确到0.01m/s)。

2、（7分）如图，二次函数的图象与x轴交于A（－1，0）、B（3，0）两点，且经过点C（0，－3）；

求：（1）二次函数的解析式是什么？

（2）当自变量如何时，函数值都随增大而增大？

（3）当自变量如何时，函数值都随增大而减小？

3、（7分）某商人如果将进货价为8元的商品按每件10元出售，每天可销售100件，现采用提高售出价，减少进货量的办法增加利润，已知这种商品每涨价1元其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚的利润最大？并求出最大利润．

4、（7分）如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。

(1)求S与x的函数关系式及自变量的取值范围；

(2)当x取何值时所围成的花圃面积最大，最大值是多少？

(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。

	D