丰台区2005年初三统一练习（一）
数学试卷
［考生须知］
1. 本试卷分为第I卷（机读卷）和第II卷（非机读卷）两部分，共8页。
2. 认真填写密封线内的学校、姓名和考号。
第I卷（机读卷 共44分）
［注意事项］
1. 考生要按要求在机读答题卡上作答，题号要对应，填涂要规范。
2. 考试结束，将试卷和机读答题卡一并交回。
一、选择题（共11小题，每小题4分，共44分）下列各题均有四个选项，其中只有一个是符合题意的。
1. －4的倒数是
A. －4
B. 4 C. 
D. 
2. 
的计算结果是
A. 
B. 
C. 
D. 
3. 下列运算正确的是
A. 
B. 
C. 
D. 
4. 我国国土面积约为平方千米，把用四舍五入法保留两位有效数字，并用科学记数法表示为
A. 96×105 B. 9.60×108
C. 9.6×106 D. 0.96×107
5. 下列图形中，对称轴最多的是
A. 平行四边形 B. 等腰梯形
C. 等边三角形 D. 正方形
6. 已知两圆的半径分别为2和5，圆心距为3，则两圆的位置关系是
A. 相交 B. 内含
C. 内切 D. 外切
7. 如图，ABCD是⊙O的内接四边形，E是AB延长线上一点，若∠CBE＝75°，则∠AOC等于
A. 150° B. 140°
C. 105° D. 75°
8. 如果圆锥的底面半径为4cm，高为3cm，那么它的侧面积是
A. 
B. 
C. 
D. 
9. Rt△ABC的直角边AC上有一点P（P与A、C不重合），过点P作直线截△ABC，使截得的三角形与原三角形相似，则满足条件的直线共有
A. 1条 B. 2条
C. 3条 D. 4条
10. 已知△ABC的面积是6，若BC的长为x，BC边上的高为y，则下列图象中能反映y与x之间关系的是
11. 甲、乙两班举行电脑汉字输入比赛，对参赛学生每分钟输入汉字的个数进行统计，得到下列数据：
| 班级 | 参加人数 | 中位数 | 方差 | 平均字数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论：①甲、乙两班学生成绩的平均水平相同；②乙班优秀的人数多于甲班（每分钟输入汉字大于或等于150个为优秀）；③甲班成绩的波动比乙班大。上述结论中正确的是
A. ①②③ B. ①②
C. ①③ D. ②③
第II卷（非机读卷 共76分）
二、填空题（共5小题，每小题4分，共20分）
12. 函数
中，自变量x的取值范围是____________。
13. 若菱形的两条对角线的长分别为6cm和8cm，则它的面积是____________cm2。
14. 计算
的结果是____________。
15. 如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC＝12，BD＝9，则梯形ABCD的中位线的长是____________。
16. 在日常生活中，某些建筑物的地板常用各种多边形地砖来铺砌，这种用形状相同或不同的平面封闭图形，把一块地面既无缝隙、又不重叠地全部覆盖，在几何里叫做平面镶嵌。
现有四种边长相等的正多边形：正三角形、正方形、正六边形、正八边形。
（1）若要求只用一种正多边形镶嵌，请写出可以用于平面镶嵌的所有正多边形________________________________________________；
（2）若要求用两种正多边形镶嵌，请写出两种设计方案①_______________________，②________________________（只需写出选用的正多边形即可）。
三、（共3个小题，共16分）
17. （5分）分解因式：
18. （5分）计算：
19. （6分）用换元法解方程：
四、（共2个小题，共11分）
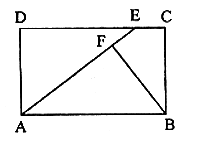
20. （5分）如图，在矩形ABCD中，E是DC边上的点，BF⊥AE于点F，且BF＝BC，请你写出图中一条和AE相等的线段，并证明你的结论。
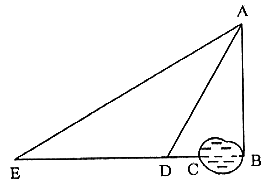
21. （6分）湖对岸有一高层建筑物，为测量湖的宽BC和建筑物的高AB，在离岸边C点10米的D处，测得∠BDA＝60°，再向外走50米到E处，又测得∠BEA＝30°（点B、C、D、E在同一直线上）。请求出湖的宽BC和建筑物的高AB（计算结果保留根号）。
五、（6分）
22. 小明家最近购买了一套住房，准备在装修时用木地板铺设卧室，用瓷砖铺设客厅。经市场调查得知：用这两种材料铺设地面的工钱不一样。小明测量了地面的面积，对铺设卧室和客厅的费用（购买材料费和工钱）分别做了预算，用x(m2)表示铺设地面的面积，用y(元)表示铺设费用，y(元)与x(m2)的关系如图所示。
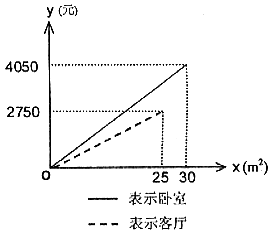
请你根据图中提供的信息，解答下列问题：
（1）预算中铺设卧室的费用为____________元/m2，铺设客厅的费用为____________元/m2；
（2）已知在小明的预算中，铺设1m2的瓷砖比铺设1m2的木地板的工钱多5元；购买1m2的瓷砖是购买1m2的木地板费用的
，问铺设瓷砖、木地板每平方米的工钱各是多少元？购买瓷砖、木地板每平方米的费用各是多少元？
六、（7分）
23. 已知关于x的方程
有两个实数根，关于x的另一个方程
的两个实数根的比为1：2，且m、n为两个不相等的正整数。求
的值。
七、（8分）
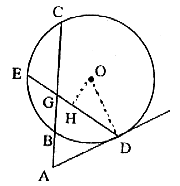
24. 如图，割线ABC与⊙O相交于B、C两点，D为⊙O上的点，E是
的中点，DE交BC于G，且∠ADG＝∠AGD。
（1）求证：AD是⊙O的切线；
（2）如果AB＝2，AD＝4，EG＝2，求⊙O的半径。
八、（8分）
25. 已知抛物线
（1）试说明对于任意实数m，抛物线都经过x轴的一个定点；
（2）设抛物线与x轴的两个交点A（x1，0）和B（x2，0）（
）分别在原点的两侧，且A、B两点间的距离小于6，求m的取值范围；
（3）抛物线的对称轴与x轴交于点C，在（2）的条件下，试判断是否存在m值，使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D，且⊙M被x轴截得的劣弧与
是等弧。若存在，求出满足条件的m的值；若不存在，请说明理由。
【试题答案】
一、选择题（共11个小题，每小题4分，共44分）
1. D 2. B 3. D 4. C 5. D
6. C 7. A 8. B 9. C 10. B
11. A
二、填空题（共5个小题，每小题4分，共20分）
12. 
13. 24
14. 
15. 
16. （1）正三角形、正方形、正六边形；
（2）参考答案：①正三角形和正方形 ②正三角形和正六边形 ③正方形和正八边形。
说明：（1）、（2）小题各2分。
三、（共3个小题，共16分）
17. （5分）
解：
1分
3分
5分
18. （5分）
解：
2分
3分
4分
5分
19. （6分）
解：设
，那么
，
于是原方程变形为 
1分
方程的两边都乘以y，约去分母，并整理，得
2分
解这个方程，得
3分
当
时，
，
解这个方程，得 
4分
当
因为
，所以，这个方程没有实数根 5分
经检验，都是原方程的根。
∴原方程的根是6分
四、（共2个小题，共11分）
20. 结论AE＝AB（或AE＝DC） 1分
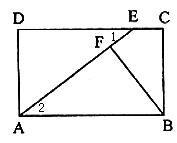
证明：∵四边形ABCD是矩形，
∴AD＝BC，AB∥DC，∠D＝90°， 2分
∴∠1＝∠2
∵BF＝BC，
∴AD＝BF 3分
∵BF⊥AE，∴∠AFB＝90°，
∴∠D＝∠AFB
在△ADE和△BFA中，
∴△ADE≌△BFA 4分
∴AE＝AB 5分
说明：AD＝BC，AB∥DC，∠D＝90°中写出任何一个即得1分。
21. 解：∵∠BDA是△ADE的外角，
∴∠BDA＝∠EAD＋∠E
∵∠BDA＝60°，∠BEA＝30°，
∴∠DAE＝60°－30°＝30°
∴∠BEA＝∠DAE 1分
∴AD＝ED＝50 2分
依题意 AB⊥BE于B
在Rt△ADB中，∠BAD＝90°－60°＝30°
∴
3分
∴BC＝25－10＝15（米） 4分
∵
∴AB＝AD·sin60°
∴
（米） 6分
所以湖的宽是15米，建筑物的高是
米。
五、（6分）
解：（1）135，110 1分
（2）解：设铺木地板的工钱为每平方米x元，购买木地板的费用为每平方米y元，则铺瓷砖的工钱为每平方米(x＋5)元，购买瓷砖的费用为每平方米y元。
根据题意，得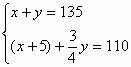
解得 
4分
所以
5分
答：铺设瓷砖和木地板的工钱分别为每平方米20元和15元；购买瓷砖和木地板的费用各是每平方米90元和120元 6分
六、（7分）
23. 解：设方程的一个根为x1，则另一根为2x1
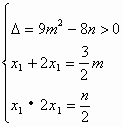1分
解得
①
2分
∵方程有两个实数根，
∴
② 3分
①代入②，得
∴
4分
∵m为正整数，∴m＝1，2
当m＝1时，n＝1，不符合题意，舍去；
当m＝2时，n＝4 6分
∴
7分
七、（本题8分）
24. 解：（1）证明：连结OE，交AC于F，连结OD
∵OE＝OD，∴∠OED＝∠ODE
∵E是的中点，OE是⊙O的半径，
∴OE⊥BC于F 2分
∴∠EGF＋∠OED＝90°
∵∠EGF＝∠AGD，∠ADG＝∠AGD
∴∠ADG＝∠EGF
∴∠ADG＋∠ODE＝90°
∴OD⊥AD
∴AD为⊙O的切线 3分
（2）∵AD切⊙O于D，ABC是⊙O的割线，
∴AD2＝AB·AC
∵AD＝4，AB＝2
∴AC＝8
∵∠ADG＝∠AGD，∴AG＝AD＝4
∴CG＝4，BG＝2 5分
∵弦ED、BC相交于点G，
∴EG·GD＝CG·BG
∵EG＝2，∴2GD＝8，∴GD＝4 6分
∴AD＝AG＝GD，∴△ADG为等边三角形
∴∠ADG＝60°
作OH⊥ED于H，则HD
∵∠ODA＝90°，∴∠ODH＝30° 7分
在Rt△OHD中，
8分
∴⊙O的半径为
。
八、（本题8分）
25. 解：（1）取y＝0，则
∴
因此对任意实数m，抛物线都经过x轴上的一个定点（2，0）
（2）∵由（1）及
可知，
∴
∴
3分
∵
∵
∴
，解得
因此，所求的m的取值范围是
5分
（3）依题意C（
）
设存在m的值，使⊙M符合要求，这时有下列两种情况：
①点C在原点的右侧，这时
⊙M过点C和点B（如图1）
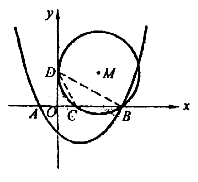
图1
连结BD、CD
∵OD切⊙M于D，∴∠CBD＝∠CDO
∵
，∴∠CBD＝∠CDB
∵∠DOC＝90°，∴∠CBD＋∠CDO＋∠CDB＝90°
∴∠CBD＝∠CDO＝∠CDB＝30°
在Rt△OBD和Rt△OCD中，
∴
，符合题意 6分
②点C在原点的左侧，这时
，⊙M过点C和点A（如图2）
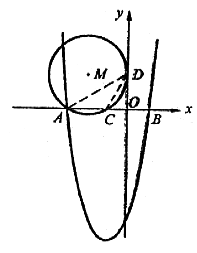
图2
连结AD、CD
与①同理得∠CAD＝∠CDO＝∠CDA＝30°
∴
，不符合题意 7分
综上所述，8分