新塘边初中九年级数学月考试卷
一、填空题(每空4分,共40分)
1. 若关于x 的方程![]() 有一根是0,则
有一根是0,则![]() ;
;
2. 若点P(![]() , 1)在第二象限,则点B(
, 1)在第二象限,则点B(![]() ,―1)必在第 象限;
,―1)必在第 象限;
3. 双曲线![]() 经过点(2 ,―3),则k =
;
经过点(2 ,―3),则k =
;
 4.等腰△ABC一腰上的高为
4.等腰△ABC一腰上的高为![]() ,这条高与底边的夹角为60°,则△ABC的面积 ;
,这条高与底边的夹角为60°,则△ABC的面积 ;
5.如图是置于水平地面上的一个球形储油罐,小敏想测量它的半
径.在阳光下,他测得球的影子的最远点A到球罐与地面接触点B
的距离是10米(如示意图,AB=10米);同一时刻,他又测得竖直
立在地面上长为1米的竹竿的影子长为2米,那么,球的半径是___________米;
6.菱形的两条对角线的长的比是2 : 3 ,面积是![]() ,则它的两条对角线的长分别为___________
,则它的两条对角线的长分别为___________
7.在阳光的照射下,直立于地面的竹竿的影子的变化情况是 ;
8.请写出一个根为![]() ,另一根满足
,另一根满足![]() 的一元二次方程
的一元二次方程
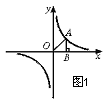
9.如图1,反比例函数图象上一点A,过A作AB⊥![]() 轴于B,
轴于B,
若S△AOB=3,则反比例函数解析式为______ ___;
 |  | ||
第10题图
10.如图,在△ABC中,BC![]() ,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是
,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是 ![]() ;
;
二.选择题(本题有10小题,每小题4分,共40分)
11.下列方程中,是关于![]() 的一元二次方程的是
( )
的一元二次方程的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
12.一元二次方程![]() 的解是
( )
的解是
( )
A、 ![]() B、
B、 ![]() C、
C、![]() ,
,![]() D、
D、![]() ,
,![]()
13.若点(1,2)同时在函数![]() 和
和![]() 的图象上,则点(
的图象上,则点(![]() ,
,![]() )为
( )
)为
( )
A.
(![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() )
C .(
)
C .(![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
14.小明用两根同样长的竹棒做对角线,制作四边形的风筝,则该风筝的形状一定是( )
A 矩形 B 正方形 C 等腰梯形 D 无法确定
15.如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )
 |

A B C D
16.一件产品原来每件的成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低成本 ( )
A、 8.5% B、 9% C、 9.5% D、 10%
17.若点(-2,y1), (1,y2), ( 2,y3)都在反比例函数,![]() 的图象上,则下列结论正确的是 ( )
的图象上,则下列结论正确的是 ( )
![]()
18.在下列四个函数中,![]() 随
随![]() 的增大而减小的函数是
( )
的增大而减小的函数是
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
19.关于四边形ABCD:①两组对边分别平行②两组对边分别相等③有两组角相等④对角线AC和BD相等 以上四个条件中,可以判定四边形ABCD是平行四边形的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
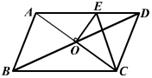 20.如图,□ABCD的周长为
20.如图,□ABCD的周长为![]() ,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为 ( )
,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为 ( )
A 4 ![]() B
6
B
6 ![]() C 8
C 8 ![]() D 10
D 10 ![]()
三、用适当的方法解下列方程:(每题5分,共20分)
21.⑴ ![]() ⑵
⑵
![]()
(3)![]() (4)
(4)![]()
四、解答题:
 22.(8分)如图,□ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。
22.(8分)如图,□ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。
(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明。
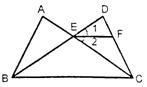
23.如图,AB = DC,AC = BD,AC、BD交于点E,过E点作EF//BC交CD于F。
求证:∠1=∠2。(8分)
24.(4分))三根垂直地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图所示。试确定路灯灯炮的位置,再作出甲的影子。(不写作法,保留作图痕迹)
 |
 25.(10分)如图,Rt△ABO的顶点A是双曲线
25.(10分)如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥![]() 轴于B且S△ABO=
轴于B且S△ABO=![]()
(1)求这两个函数的解析式
(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。
26、已知:如图,△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE。
(1)猜想:DF与AE有什么关系?证明你的猜想(5分).
(2)若BE⊥AC,AD与DE有什么关系?证明你的结论(5分).

27、宏达水果商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,出售价格每涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?(10分)