温州市“五校联考”九年级学业评价(2006.4)
数学试卷
一.选择题(本小题有10小题,每小题4分,共40分)
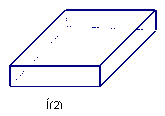
1.如图所示的几何体,它的主视图是 ( )

(第1题) A. B. C. D.
2.下列运算中,正确的是 ( )
A a3·a4=a12 B a4+a4=a8 C a8÷a4=a4 D (―2a2)3=―2a6
|
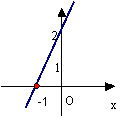
A ![]() B
B
![]() C
C ![]() D
D ![]()
4.两圆的半径分别为3和5,圆心距为8,则两圆的位置关系是( )
A 内含 B 相交 C外切 D 内切
5.小明的身高为1.8米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树的影长为6米,则这棵树的高为( )
A. 3.2米 B.4.8 米 C. 5.4 米 D.5.6米
6.为筹备班级的成长毕业联欢会,班长对全班学生喜欢那种水果进行民意调查,以决定最终买什么水果,下面的调查数据中最值得关注的是 ( )
A 中位数 B 平均数 C 众数 D 方差
7.圆锥的母线长为8cm,底面半径为6cm,则圆锥的侧面积是 ( )
 A.96πcm2 B.60πcm2
C.48πcm2 D.24πcm2
A.96πcm2 B.60πcm2
C.48πcm2 D.24πcm2
|
A ![]() B
B ![]()
C ![]() D
D ![]()
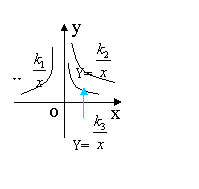 9.如图是三个反比例函数
9.如图是三个反比例函数![]() 在x轴上方的图像,由此观察得到k1,k2,k3大小关系为 ( )
在x轴上方的图像,由此观察得到k1,k2,k3大小关系为 ( )
A k1 > k2 > k3
B k2 > k3 > k1
C k3 > k2 > k1
D k3 > k1 > k2
 10.将一张正方形的纸片按下图所示的方式三次折叠,折叠后再按图所示沿MN裁剪,则可得( )
10.将一张正方形的纸片按下图所示的方式三次折叠,折叠后再按图所示沿MN裁剪,则可得( )
A. 多个等腰直角三角形 B. 一个等腰直角三角形和一个正方形
C.四个相同的正方形 D.两个相同的正方形
二.填空题(本小题有6小题,每小题5分,共30分)
 11.“神舟五号”载人飞船的发射成功标志着我国航天工业迅猛发展,据报载,有关数据计算精确度越来越高,发射偏差仅为0.,这个数用科学记数法应表示为_____________.
11.“神舟五号”载人飞船的发射成功标志着我国航天工业迅猛发展,据报载,有关数据计算精确度越来越高,发射偏差仅为0.,这个数用科学记数法应表示为_____________.
12.不等式![]() 的正整数解是
.
的正整数解是
.
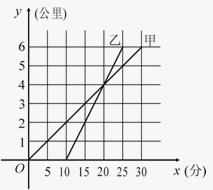
13.甲骑自行车、乙骑摩托沿相同路线由A地到
B地,行驶过程中路程与时间的函数关系的图象如
图所示。根据图象可知:
①先出发的是 (填“甲”或“乙”)
②乙的行驶速度是 (公里 / 分)
 14.用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:
14.用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:
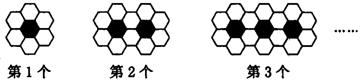
则第![]() 个图案中有白色地面砖
块.
个图案中有白色地面砖
块.
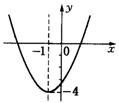
15.二次函数![]() 的图象如图所示,
的图象如图所示,
则![]() 的两根分别是
.
的两根分别是
.

16.如图,作等边△ABC,取AC的中点D,以AD为边
向△ABC形外作等边△ADE,取AE的中点G,再以EG
为边作等边△EFG,如此反复,当作出第6个三角形时,
若AB=4,整个图形的外围周长是 .
三.解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17.计算![]()
18.解方程: ![]()
19.在平行四边形ABCD中,![]() 和
和![]() 的平分线交于M,DM的延长线交AD于E,
的平分线交于M,DM的延长线交AD于E,
试猜想(1)CM与DE的位置关系?(2)M在DE的什么位置上?并证明你的猜想.
 |
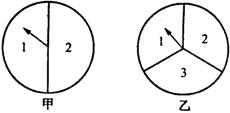 20.小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,当两个转盘所转到的数字之积为奇数时,小明得2分;当所转到的数字之积为偶数时,小刚得1分。这个游戏对双方公平吗?若公平,说明理由。若不公平,如何修改规则才能使游戏对双方公平?
20.小明和小刚用如图所示的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,当两个转盘所转到的数字之积为奇数时,小明得2分;当所转到的数字之积为偶数时,小刚得1分。这个游戏对双方公平吗?若公平,说明理由。若不公平,如何修改规则才能使游戏对双方公平?
21.如图21—1,一个圆球放置在V形架中.图21—2是它的平面示意图,
CA和CB都是⊙O的切线,切点分别是A,B.如果⊙O的半径为![]() cm,
cm,
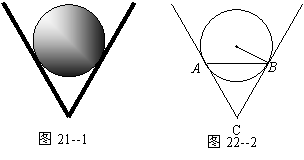 且AB=6cm,求∠ACB.
且AB=6cm,求∠ACB.
22.画一个正方体的三种平面展开图,要求展开图是中心对称图形。
(画出的图是正方体的展开图,但不是中心对称图形每种可得2分。)
 |  |  |
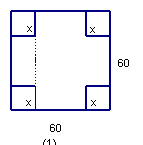
23.用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:
如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形(如图1),然后把四边折合起来(如图2)。①求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;②当做成的盒子的底面积为900㎝2时,试求该盒子的容积。
 |  | ||
24.把两个全等的直角三角板ABC和EFG叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF长均为4.(1)当 EG⊥AC于点K,GF⊥BC于点H时(如图①),求GH:GK的值
 (2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转,旋转角α满足条件:0°<α<30°(如图②),EG交AC于点K ,GF交BC于点H,GH:GK的值是否改变?证明你发现的结论;(3)三角板EFG由图①所示的位置绕O点逆时针旋转一周,是否存在某位置使△BFG是等腰三角形,若存在,请直接写出相应的旋转角α(精确到0.1°);若不存在,说明理由.
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转,旋转角α满足条件:0°<α<30°(如图②),EG交AC于点K ,GF交BC于点H,GH:GK的值是否改变?证明你发现的结论;(3)三角板EFG由图①所示的位置绕O点逆时针旋转一周,是否存在某位置使△BFG是等腰三角形,若存在,请直接写出相应的旋转角α(精确到0.1°);若不存在,说明理由.
温州市“五校联考”九年级学业评价(2006.4)
数学试卷参考答案
一.选择题(每小题4分共40分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| C | B | C | C | C | C | A | B | C |
二.填空题(每小题5分共30分)
11. 1.04×10-5
12.x=1 13 . 甲 0.4 14. 4n+2 15.-3,1 16. ![]()
三.解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17.(本题8分)
解:原式=1+3-5-1 ---------------------4分
=4-6 ---------------------------2分
= -2 --------------------------2分
18. (本题8分)
解:去分母得x-5=2(2x-1)----------------3分
∴3x=-3 ------------------------2分
∴x=-1 ---------------------------1分
经检验原方程的根是x=-1 -----------2分
19.(本题8分)
. 解:(1) CM⊥DE ----------------------------------1分
∵ AD∥BC∴∠ADC+∠BCD=180°-----1分
∵DE,CM分别平分∠ADC, ∠BCD
∴∠MDC+∠MCD=90°∴CM⊥DE------2分
(2)M为ED的中点 ----------------------------1分
∵AD∥BC∴∠ADE=∠CEM
∵∠ADE=∠CDE∴∠CDE=∠CED--------1分
∴CD=CE
∵CM⊥DE∴EM=MD-------------------------2分
20. (本题8分)
.解:公平。 ----------------------------------------------------------------------2分
将两个转盘所转到的数字求积:从表中可以得到:
![]() ,
,![]() ,
-------------------------------------------3分
,
-------------------------------------------3分
小明的积分为![]() ,小刚的积分为
,小刚的积分为![]() .
.
∵小明的积分=小刚的积分为 ∴公平. ---------------- ----------------------------3分
21、(本题10分)
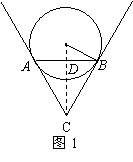 解:如图1,连结OC交AB于点D。 ---------------------1分
解:如图1,连结OC交AB于点D。 ---------------------1分
∵CA,CB分别是⊙O的切线,
∴CA=CB,OC平分∠ACB,∴OC⊥AB。 ----------3分
∵AB=6,∴BD=3。在Rt△OBD中,![]()
![]() ---------3分
---------3分
∵B是切点,∴OB⊥BC,
∴∠OCB=30°
∴∠ACB=60°. --------------------------------------------3分
22.(本题12分)画对一种得4分,画出的图形是正方体的展开图,但不是中心对称图形的每种可得2分
 |
23.(本题12分)
解:(1)y=(60-2x)2
即y=4x2-240x+3600 -----------------------------4分
(2)当y=900时(60-2x)2 =900 -------------------1分
∴60-2 x=±30
∴x1=15 x2=45 ---------------------------------3分
∵x2=45不符合题意∴x=15 ---------------------------------------1分
∴该盒子的容积为900×15=13500 ----------------------------------2分
答:该盒子的容积为13500cm3 ------------------------------------------------------------1分
24.(本题14分)(1) GH:GK=![]() -----------------------------------3分
-----------------------------------3分
(2)不变, --------------------------------------------------------------------1分
过G作GM⊥AC于M GN⊥BC于N
易证⊿GMK∽⊿GNH
∴GH:GK=GN:GM=![]() ----------------------------------------5分
----------------------------------------5分
(3)存在,----------------------------------------------------------------------------------------------------1分
30°、90°、133.2°或346.8°-----------------------------------4分