2005年初中毕业生学业考试
模拟数学试卷
文锦中学 刘艳辉
说明：全卷七大题，共8页，考试时间90分钟，满分100分．
一、选择题（本题有10小题，每题3分，共30分）
每小题给出4个答案，其中只有一个是正确的．
1 某物体的三种视图如图（1）所示，那么该物体的 （ ）
形状是
A 长方体
B 立方体
C 圆柱体 D 圆锥体
图（1）
2 第五次全国人口普查结果显示，我国的总人口已达到1 300 000 000人，用科学记数法表示这个数，结果正确的是 （ ）
A．1.3×108 B．1.3×109 C．0.13×1010 D．13×109
3 要使代数式3x+
有意义，字母x必须满足的条件是
（ ）
A．x≥1 B．x＞－1 C．x≥－1 D．x＞1
4 如图，从几何图形的角度看，下列这些图案既是中心对称图形又是轴对称图形的是（ ）
A
B 
C 
D
5
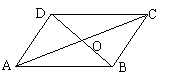如图，□ABCD中，对角线AC和BD相交于点O，如果
AC=26,BD=18,AB=x,那么x的取值范围是 （ ）
A、4< m <13 B、4< m <22
C、9< m <13 D、4< m <9
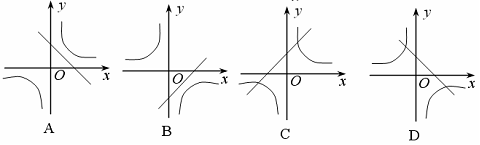
6 在同一直角坐标系中，函数y=kx-k与
(k≠0)的图象大致是
（ ）
7 已知在⊙O中，弦AB的长为8厘米,圆心O到AB的距离为3厘米,则⊙O的半径是
（ ）
A 3厘米 B 4厘米 C 5厘米 D 6厘米
8 某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不可以是 （ ）
A. 正三角形 B 矩形 C 正八边形 D 正六边形
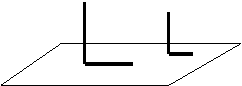
9 如图所示，是两木杆在同一时刻的影子，请问它们是太阳光线还是灯光下的投影？请问这一时刻是上午还是下午？ （ ）
A、太阳光线，上午 B、太阳光线，下午 C、灯光，上午 D、 灯光，下午
北
东
西
南
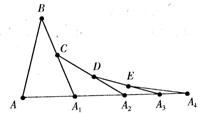
10. 如图，已知AB=A1B，A1C=A1A2，A2D=A2A3，A3E=A3A4，若∠B=20°，则∠A —
∠A4 .
A 80°,40° B 80°,30° C 80°,20° D 80°,10°
二、填空题（本题有5小题，每题3分，共15分．）
11用估算的方法求一元二次方程2t2-t-2=0的解
列表：
| t | 0 | 1 | 2 | 3 |
| 2t2-t-2 | -2 | -1 | 4 | 13 |
∴ t ≈
12 有一个盒子中有12张空白卡和若干张标有记号的卡片，每张卡片除记号外完全相同。从盒子中随机地取出一张卡片，记下其是否有记号，再放回盒子中，不断重复上述过程，共摸了200次，其中50次取出的卡片上有记号，则估计其中有记号的卡片 张。
13 一次数学知识竞赛共有20道题,规定答对一道题得10分,答错或不答一道题得-5分,在这次竞赛中,小明获得一等奖(150分或150分以上),则小明至少答对了__________道题.
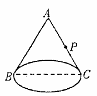14 如图，有一圆锥形粮堆，其正视图是边长为4m的正三角形ABC，粮堆母线AC的中点P处有一老鼠正在偷吃粮食，此时，小猫正在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的最短路程是
m（结果不取近似值）。
15 如图，□ABCD中，AE、CF分别是∠BAD和∠BCD的角平分线根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是 （只需写出一个即可，图中不能再添加别的“点”和“线”）
三、计算题：(本题满分14分)
16 计算：
(本题4分)
17
化简，求值：
，其中
(本题4分)
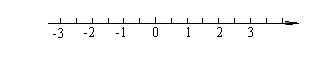
18 解不等式组(本题6分)
解不等式组 并把解集在数轴上表示出来.
 |
四 作图题（保留作图痕迹，写出作法）(本题满分5分)
19 已知：如图（5）三条公路两两分别相交于点A、B、C，在甲区内求作一点P，使点P到三条公路的距离都相等。
作法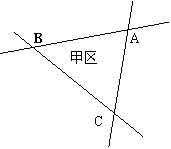
：
五 解答题 (本题满分36分)
20 (本题6分) 为缓解用电紧张矛盾，某电力公司特制定了新的用电收费标准，每月用电量x (度)付电费 y(元)的关系如图所示．
(1)根据图象，请分别求出当0≤x≤50和x≥50时，y与x的函数关系式．
(2)当每月用电量不超过50度和用电量超过50度时的收费标准各是多少？
 |
归纳与猜想
21．(本题6分)
问题：你能很快算出20052吗？为了解决这个问题，我们考查个位上的数字为5的自然数的平方，任意一个个位数字为5的自然数都可写成10n+5，即求（10n+5）2的值（n为自然数）。试分析n=1，n=2，n=3，…，这些简单情况，从中探索其规律，并归纳、猜想出结论（在下面空格内填上你的探索结果）。
（1）通过计算，探索规律：
152可写成100×1（1+1）+25，
252可写成100×2（2+1）+25，
352可写成100×3（3+1）+25，
452可写成100×4（4+1）+25，
…
752可写成 ，
852可写成 。
（2）从第（1）题的结果归纳，猜想，得（10n+5）2= ，
（3）根据上面的归纳、猜想，请计算：
20052=
22 (本题6分).
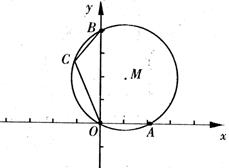
如图，⊙M经过原点且与两坐标轴分别交于点A和点B，点A的坐标为（4，0），C是圆上一点，∠BCO=120°，求⊙M的半径和圆心M的坐标。
23、(本题8分).
未成年人思想道德建设越来越受到社会的关注。某青少年研究所随机调查了我市某校100名学生寒假中花零花钱的数量(钱数取整数元)，以便引导学生树立正确的消费观。根据调查数据制成了频率分布表和频率分布直方图(如图7)。
| 分组 | 频数 | 频率 |
| 0.5~50.5 | _______ | 0.1 |
| 50.5~______ | 20 | 0.2 |
| 100.5~150.5 | _______ | ______ |
| ______200.5 | 30 | 0.3 |
| 200.5~250.5 | 10 | 0.1 |
| 250.5~300.5 | 5 | 0.05 |
| 合计 | 100 | ________ |
⑴补全频率分布表；
⑵在频率分布直方图中，长方形ABCD的面积是_________；这次调查的样本容量是_________；
⑶研究所认为，应对消费150元以上的学生提出勤俭节约的建议。试估计应对该校1000名学生中约多少名学生提出这项建议？
综合探究题
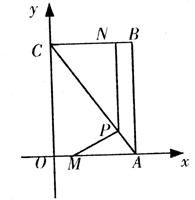
24．(本题满分10分)如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0），（3，4）。动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中点M沿OA 向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于P，连接MP，已知动点运动了x秒。（1）求点P的坐标（用含x的代数式表示）。（2）试求△MPA面积的最大值，并求此时x的值。（3）请你探索：当x为何值时，是一个等腰三角形？你发现了几种情况？写出你的探索结果。
2005年初中毕业生学业考试
模拟数学试卷答案
文锦中学 刘艳辉
一 选择题：
DBCAB DCCAD
二 填空题:
11.1
12.3
13.17
14.
15.AC⊥EF（答案不唯一）
三 计算题：
16．-7
17．2x+4,2
18．X≥3（数轴略）
四、作图题
19. 略
五、解答题
20. (1) ①当月用电量0≤x≤50时，
是
的正比例函数．
设
，∵当
时，
，
∴
， ∴
．
∴
。
②当月用电量x≥50时，是的一次函数．
设
， ∵当时，；当
时，
．
∴
∴
∴
．
(2) 当每月用电量不超过50度时，收费标准是: 每度0.50元．
当每月用电量超过50度时，收费标准是: 其中的50度每度0.5元，超过部分每度0.9元。
21. (1)100×7(7+1)+25,100×8(8+1)+25,
(2)100×10n(10n+1)+25,
(3)100×200(200+1)+25=.
22. 连结AB，∵BO⊥AO，∴AB过圆心M,AB是⊙M的直径.
∵∠BCO=120°, ∠BOA=90°
∴∠ABO=30°
在Rt△ABO中,AB=2OA=8, ∴⊙M的半径为4.
∵在Rt△ABO中，BO=
,过M作MN⊥AO，垂足为N.
∵M是中点，
∴MN=
,ON=2
∴⊙M的圆心的坐标为(2, ).
23. (1)100.5,150.5,10,25,0.25,1.00
(2)0.25,100
(3)(0.3+0.1+0.05)×1000=450
综合探究题
24.解:(1) P(3-x,
x)
(2) 设△MPA的面积为S,在△MPA中,MA=3-x,MA边上的高为x ，
其中0≤x≤3
S=
∴S的最大值为
。此时，x=
（3） 延长NP交x轴于Q，则有PQ⊥OA ,
①若MP=PA,
∵PQ⊥MA，∴MQ=QA=x
∴3x=3,x=1
②若MP=PA,则MQ=3-2x,PQ=
,PM=MA=3-x,
在Rt△PMQ中，∵PM2=MQ2+PQ2
∴
，∴
③若PA=AM, ∵PA=
，AM=3-x,
∴
,∴x=
综上所述，x=1或x=
或x=