余杭区九年级质量检测卷——数学试题
| 题号 | 一 | 二 | 三 | 总 分 | |||
| 17～19 | 20、21 | 22、23 | 24 | ||||
| 得分 | |||||||
一、选择题（本大题共10个小题，每小题4分，共40分，请选出各题中一个符合题意的正确选项，不选择，多选，错选，均不给分）
1． 
的相反数是( ).
A．5 B．
C．-5 D．
2． 某服装销售商在进行市场占有率的调查时，他最应该关注的是( ).
A. 服装型号的平均数 B. 服装型号的众数
C. 服装型号的中位数 D. 最小的服装型号
3． 如图，几何体的俯视图是( ).
 |
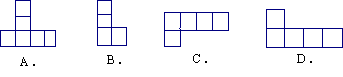4． 某闭合电路中，电源的电压为定值，电流I（A）与电阻R（Ω）成反比例．如图表示的是该电路中电流I与电阻R之间函数关系的图像，则用电阻R表示电流I的函数解析式为( ).
A．
B．
C．
D．
5. 抛物线
的顶点坐标是( ).
A.(0，-2) B.(-2，0) C.(0，2) D.(2，0)
6. 如图，小正方形的边长均为l，则下列图中的三角形(阴影部分)与△ABC相似的是( ).
7. 四张完全相同的卡片上，分别画有圆、矩形、等边三角形、等腰梯形，现从中随机抽取一张，卡片上画的恰好是中心对称图形的概率为( ).
| |
B．
C．
D．1
8. 如图，A、C、B是⊙O上三点，若∠AOC＝40°，则∠ABC的
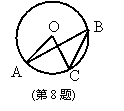度数是( ).
A．10° B.20° C.40° D.80°
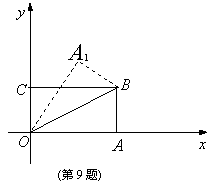9．如图，在直角坐标系中，将矩形
沿
对折，使点
落在点
处，已知
,
，则点的坐标是（ ）．
A．（
，
） B．（，3）
C．（，） D．（，）
10. 二次函数
的图象，如图7所示，若
，
,则( ).
A.
B.
C.
D.
二、填空题（本题有6个小题，每题5分，共30分）
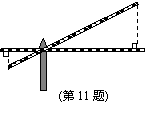
11. 如图，铁道口栏杆的短臂长为1.2m，长臂长为8m，当短臂端点下降0.6m时，长臂端点升高 m（杆的粗细忽略不计)．
12．已知一列数：1，―2，3，―4，5，―6，7，… 将这列数排成
下列形式：
第1行 1
第2行 －2 3
第3行 －4 5 －6
第4行 7 －8 9 －10
第5行 11 －12 13 －14 15
… …
按照上述规律排下去，那么第10行从左边数第5个数
等于 ．
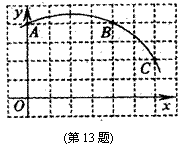
13．如图，直角坐标系中一条圆弧经过网格点A，B，C，其中B点坐标为（4，4），则该圆弧所在圆的圆心坐标为 ．
14. 如图，已知正方形ABCD的边长为2.如果将线段BD 绕着点B旋转后，点D落在CB的延长线上的D′点处，那么
tan∠BAD′等于__________．
15. “十一”黄金周期间，某风景区在7天假期中对每天上山旅游的
人数统计如下表：
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数（万人） | 1.2 | 1.2 | 2.3 | 1.8 | 1.8 | 1.2 | 0.8 |
这7天中上山旅游人数的众数是________万人，中位数是
________万人．
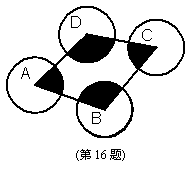
16. 如图，在四边形ABCD中，四条边均大于2，以1为半径，分别以A、B、C、D为圆心作圆，则图中阴影部分的面积为 ．
三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17．计算： 
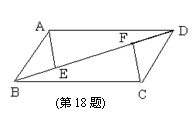
18. 如图，在平行四边形ABCD中，点E、F在对角线BD上，且BE = DF，求证：AE = CF
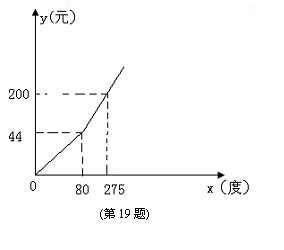19．去年以来，浙江大部分地区的电力紧缺，电力公司为鼓励市民节约用电，采取按月用电量分段收费办法，若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：
（1）分别写出当0≤x≤80和x≥80时，y与x的
函数关系式；
（2）若该用户某月用电62度，则应缴费多少元？
若该用户某月缴费220元时，则该用户该月用
了多少度电？
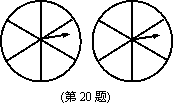
20．如图，用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(一个转盘转出“红”，另一个转盘转出“蓝”，则为配成紫色).在所给转盘中的扇形里，分别填上“红”或“蓝”，使得到紫色的概率是
.
21．市体校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛．他们的成绩（单位：m）如下：
甲：1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙：1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲、乙两名运动员的跳高平均成绩分别是多少？
(2)哪位运动员的成绩更为稳定？
(3)若预测，跳过1.65m就很可能获得冠军，该校为了获得冠军，可能选哪位运动员参赛？若预测跳过1.70m才能得冠军呢？
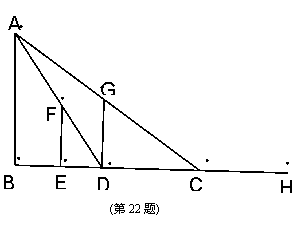
22．小明和小斌在路灯A下在行走，两人想测量一下路灯的高度．两人在站在同一直线BH上，已知小明身高1. 50米，小斌身高1.60米；两人在同一点E处测得小明的影长为1米，小斌向BH方向行走了1米到达D处，测得影长为1.6米，请你帮忙计算出路灯的高度．
 |
23．某城市为开发旅游景点，需要对古运河重新设计，加以改造，现需要A、B两种花砖共50万块，全部由某砖瓦厂完成此项任务．该厂现有甲种原料180万千克，乙种原料145万千克，已知生产1万块A砖，用甲种原料4.5万千克，乙种原料1.5万千克，造价1.2万元；生产1万块B砖，用甲种原料2万千克，乙种原料5万千克，造价1.8万元．
（1）利用现有原料，该厂能否按要求完成任务？若能，按A、B两种花砖的生产块数，有哪几种生产方案？请你设计出来（以万块为单位且取整数）；
（2）试分析你设计的哪种生产方案总造价最低？最低造价是多少？
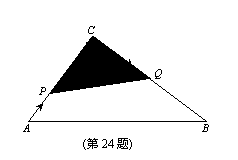
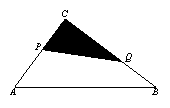
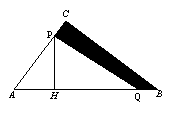
24．已知：如图，△ABC中，∠C＝90°，AC＝3厘米，CB＝4厘米．两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动．当点Q运动到点A时，P、Q两点运动即停止．点P、Q的运动速度分别为1厘米/秒、2厘米/秒，设点P运动时间为t（秒）．
（1）当时间t为何值时，以P、C、Q三点为顶点的三角形的面积（图中的阴影部分）等于2厘米2；（3分）
（2）当点P、Q运动时，阴影部分的形状随之变化．设PQ与△ABC围成阴影部分L，问何时阴影部分L为三角形？问何时阴影部分L为四边形？（4分）
以下两个小题请任选一题，两题都答则以第一题为准(A题满分为7分，B题满分为10分）
（A）当点P、Q运动时，阴影部分的形状随之变化．设PQ与△ABC围成阴影部分面积为S（厘米2），求出S与时间t的函数关系式，并指出自变量
的取值范围；
（B）点P、Q在运动的过程中，阴影部分面积S有最大值吗？若有，请求出最大值；若没有，请说明理由．
余杭区九年级质量检测卷——数学试题参考答案
一、选择题（每题满分4分，共40分）：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | C | C | D | B | B | B | A | D |
10． 提示当
时，
，对称轴
二、填空题（每题满分5分，共30分）：
11．4 12.－50 13.（2,0） 14.
15. 1.2; 12 16.
（提示：阴影部分面积组成一个圆的面积）.
三、简答题：
17．（每题满分8分）原式=
=－8；……8分
18．（每题满分8分）证明：∵四边形ABCD是平行四边形
∴AB=CD，AB∥CD……2分
∴∠ABE=∠CDF……2分
又∵BE=DF∴△ABE≌△DCF……2分
∴AE=CF……2分
19．（每题满分8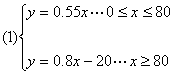分）
………4分
(2) 34.1元；300度 ………4分
20. （每题满分8分）解：如图，一个转盘的六个扇形都填“红”，另一个转盘的一个
扇形填“蓝”，余下的五个扇形不填或填其它色. ……8分
(注：一个填两个“红”，另一个填三个“蓝”等也可) ……8分
21．（每题满分10分）（1)
………3分
（2）
， 
………2分
故甲稳定 ………2分
（3）可能选甲参加，因为甲8次成绩都跳过1.65m而乙有3次低于1.65m 也可能选乙参加，因为甲仅3次超过1.70m，当然学生可以有不同看法只要有道理. ….3分
22．（每题满分12分）在Rt△A BC中，∠ABC＝90°，
，
，………4分
同理可得：
………4分
解得AB＝4.8，BE＝2.2 故路灯高为4.8米。………4分
23．（每题满分12分）解：（1）利用现有原料能完成生产任务。
设生产A种砖x万块，则生产B种砖（50－x）万块，………1分
依题意
解得 
………4分
故利用现有原料能完成生产任务，且有以下三种生产方案：
①生产A种砖30万块，B种砖20万块；………1分
②生产A种砖31万块，B种砖19万块；………1分
③生产A种砖32万块，B种砖18万块。………1分
（2）总造价M＝1.2x＋1.8（50－x）＝90－0.6x……2分
因此，第三种方案生产总造价最低，应为90－0.6×32＝70.8（万元）。
………2分
24、（本题满分14分）
解：（1）S△PCQ＝
PC·CQ＝
＝
＝2， ………1分
解得 
＝1，
＝2
………1分
∴当时间为1秒或2秒时，S△PCQ＝2厘米2； ………1分
（2）当0＜≤2和3＜≤4.5 阴影部分L为三角形 ………2分
当2＜≤3时，阴影部分L为四边形。 ………2分
（A）①当0＜≤2时，S＝
＝
； ………2分
②当2＜≤3时， S＝
＝
；………3分
③当3＜≤4.5时，S＝
＝
；…2分
（B）有；
………2
①在0＜≤2时，当＝
，S有最大值，S1＝
； ………2分
②在2＜≤3时，当＝3，S有最大值，S2＝
； ………2分
③在3＜≤4.5时，当＝
，S有最大值，S3＝
； ………2分
∵S1＜S2＜S3 ∴＝时，S有最大值，S最大值＝． ………2分