26.1二次函数(A卷)
(100分 60分钟)
一、选择题:(每题4分,共28分)
1.若函数
是二次函数,那么m的值是( )
A.2
B.-1或3
C.3
D.
2.满足函数y=x2-4x-4的一个点是( )
A.(4,4) B.(3,-1);
C.(-2,-8) D. 
3.无论m为何实数,二次函数y=x2-(2-m)x+m的图象总是过定点( )
A.(1,3) B.(1,0); C.(-1,3) D.(-1,0)
4.在函数y=
中,自变量x的取值范围是( )
A.x≠1 B.x>0; C.x>0且x≠1 D.x≥0且x≠1
5.在直角坐标系中,坐标轴上到点P(-3,-4)的距离等于5的点共有( )
A.1个 B.2个 C.3个 D.4个
6.在函数y=
中,自变量x的取值范围是( )
A.x>-2且x≠-3; B.x>-2且x≠3; C.x≥-2且x≠±3; D.x≥-2且x≠3
7.下列函数中,是二次函数的是( )
A.y=8x2+1 B.y=8x+1;
C.y=
D.y=
二、填空题:(每题5分,共45分)
(1) (2) (3)
8.形如_______________的函数叫做二次函数.
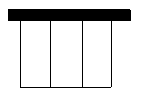
9.如图1所示,某校小农场要盖一排三间长方形的羊圈,打算一面利用一堵旧墙, 其余各面用木棍围成栅栏,该校计划用木棍围出总长为24m的栅栏. 设每间羊圈的长为xm.(1)请你用含x的关系式来表示围成三间羊圈所利用的旧墙的总长度L=_______,三间羊圈的总面积S=____________;
(2)S可以看成x的_________,这里自变量x的取值范围是_________;
(3)请计算,当羊圈的长分别为2m、3m、4m和5m时,羊圈的总面积分别为_____、_____、______、______,在这些数中,x取_____m时,面积S最大.
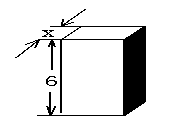
10.如图2所示,长方体的底面是边长为xcm的正方形,高为6cm,请你用含x 的代数式表示这个长方体的侧面展开图的面积S=________,长方体的体积为V=__________,各边长的和L=__________,在上面的三个函数中,_______是关于x的二次函数.
11.根据如图3所示的程序计算函数值.
(1)当输入的x的值为
时,输出的结果为________;
(2)当输入的数为________时,输出的值为-4.
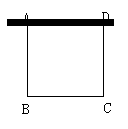
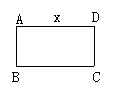12.如图4所示,要用总长为20m的铁栏杆,一面靠墙, 围成一个矩形的花圃, 若设AB的长为xm,则矩形的面积y=_______________.
13.某商店将每件进价为8元的某种商品每件10元出售,一天可销出约100件. 该店想通过降低售价、增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低0.1元,其销售量可增加10件,将这
种商品的售价降低x元时, 则销售利润y=_________.
14.函数y=
中,自变量x的取值范围是___________.
15.y=(m2-2m-3)x2+(m-1)x+m2是关于x的二次函数要满足的条件是_______.
16.如图5所示,有一根长60cm的铁丝,用它围成一个矩形,写出矩形面积S(cm2)与它的一边长x(cm)之间的函数关系式____________.
三、解答题:(27分)
17.(12分)心理学家发现,在一定的时间范围内,学生对概念的接受能力y与提出概念所用的时间x(单位:分钟)之间满足函数关系y=-0.1x2+2.6x+43(0≤x≤30),y的值越大,表示接受能力越强.
(1)若用10分钟提出概念,学生的接受能力y的值是多少?
(2)如果改用8分钟或15分钟来提出这一概念,那么与用10分钟相比,学生的接受能力是增强了还是减弱了?通过计算来回答.
18.(15分)已知正方形的周长是Ccm,面积是Scm2.
(1)求S与C之间的函数关系式;(2)当S=1cm2时,求正方形的边长;
(3)当C取什么值时,S≥4cm2?
26.1 二次函数(B卷)
(100分 90分钟)
一、学科内综合题:(每题6分,共18分)
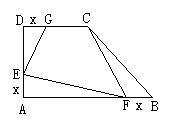
1.如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
2.如图所示,在△ABC中,AB=4
,AC=6,BC=2,P是AC上与A、C不重合的一个动点,过P、B、C的⊙O交AB于D.设PA=x,PC2+PD2=y,求y与x的函数关系式,并确定x的取值范围.
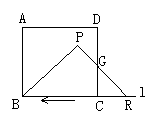
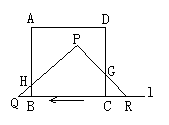
3.如图所示,有一边长为5cm的正方形ABCD和等腰三角形PQR,PQ= PR= 3cm, QR=8cm,点B、C、Q、R在同一条直线L上,当C、Q两点重合时,等腰三角形PQR以1cm/ 秒的速度沿直线L按箭头所示的方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:
(1)当t=3时,求S的值;(2)当t=5时,求S的值;
(3)当5≤t≤8时,求S与t之间的函数关系式.
二、学科间综合题:(7分)
4.一个人的血压与其年龄及性别有关,对女性来说,正常的收缩压p(毫米汞柱) 与年龄x(岁)大致满足关系式p=0.01x2+0.05x+107;对男性来说,正常的收缩压p( 毫米汞柱)与年龄x(岁)大致满足关系式p=0.006x2-0.02x+120.
(1)利用公式计算你的收缩压;
(2)如果一个女性的收缩压为120毫米汞柱,那么她的年龄大概是多少岁?(1毫米汞柱=133.3224帕)
(3)如果一个男性的收缩压为130毫米汞柱,那么他的年龄大概是多少岁?
三、应用题:(每题9分,共36分)
5.如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A 开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
6.某化工材料经销公司购进了一批化工原料共7000千克, 购进价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现,单价定为70元时,日均销售60千克;单价每降低1元,每天多售出2千克. 在销售过程中,每天还要支出其他费用500元(天数不足一天时,按一天计算).设销售单价为x元,日均获利为y元.请你求出y关于x的二次函数关系式,并注明x的取值范围.
7.某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系m=162-3x. 请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.
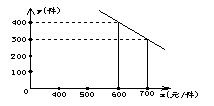
8.某公司试销一种成本单价为500元/件的新产品, 规定试销时的销售单价不低于成本单价,又不高于800元/件.试销时,发现销售量y(件)与销售价x(元/件)的关系可近似看作一次函数y=kx+b(k≠0),如图所示.
(1)根据图象,求一次函数y=kx+b的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元, 试用销售单价表示毛利润S.
四、创新题:(每题10分,共20分)
(一)教材中的变型题
9.(教材P4第3题变题)已知二次函数y=ax2+(km+c),当x=3时,y=15;当x=-2时,y=5,试求y与x之间的函数关系式.
(二)多变题
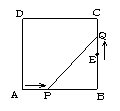
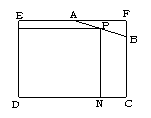
10.如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE, 其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.
五、中考题:(19分)
11.(2002,昆明,8分)某广告公司设计一幅周长为12米的矩形广告牌, 广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.
(1)求出S与x之间的函数关系式,并确定自变量x的取值范围.
(2)为使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费是多少?(精确到元)
12.(2004,黄冈,11分)心理学家研究发现,一般情况下, 学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强, 中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力y随时间t的变化规律有如下关系式:
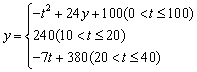
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较, 何时学生的注意力更集中?
(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
26.1 二次函数(C卷)
(30分 45分钟)
一、实践题:(10分)
1.某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产.已知生产每件产品的成本为40元, 在销售过程中发现,当销售单价定为100元时,年销售时为20万件;销售单价每增加10元, 年销售量将减少1万件.设第一年销售单价为x元,销售量为y万件,获利(年获利=年销售额-生产成本-投资)为z万元.
(1)试写出y与x之间的函数关系式;(不必写出x的取值范围)
(2)试写出z与x之间的函数关系式;(不必写出x的取值范围)
(3)计算销售单价为160元时的获利,并说明同样的获利,销售单价还可以定为多少元?相应的销售量分别为多少万件?
二、竞赛题:(每题10分,共20分)
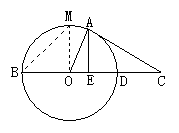
2.已知:如图所示,BD为⊙O的直径,且BD=8,
是圆周的
,A为上任意一点, 取AC=AB,交BD的延长线于C,连结OA,并作AE⊥BD于E,设AB=x,CD=y.
(1)写出y关于x的函数关系式;
(2)当x为何值时,CA是⊙O的切线?
(3)当CA与⊙O相切时,求tan∠OAE的值.
3.如图所示,△ABC中,BC=4,∠B=45°,AB=3
,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.
(1)求出S与x之间的函数关系式,并写出自变量x的取值范围.
(2)是否存在平行于BC的线段MN,使△MNC的面积等于2?若存在,请求出MN的长; 若不存在,请说明理由.
二次函数A卷答案:
一、1.C 2.D 3.C 4.D 5.C 6.D 7.A
二、8.y=ax2+bx+c(a、b、c为常数,a≠0)
9.(1)-4x+24;-4x2+24x
(2)二次函数;0<x<6
(3)32m2;36m2;32m2;20m2;3
10.24x;6x2;8x+24;V=6x2
11.(1)
(2)6或-6
12.y=-2x2+20x(0<x<10)
13.y=-100x2+100x+200(0≤x≤2)
14.x>3且x≠5
15.m≠-1且m≠3
16.S=-x2+30x(0<x<30)
三、17.解:(1)当x=10时,y=-0.1x2+2.6x+43=-0.1×102+2.6×10+43=59.
(2)当x=8时,y=0.1x2+2.6x+43=-0.1×82+2.6×8+43=57.4,
∴用8分钟与用10分钟相比,学生的接受能力减弱了;
当x=15时,y=-0.1x2+2.6x+43=-0.1×152+2.6×15+43=59.5.
∴用15分钟与用10分钟相比,学生的接受能力增强了.
18.解:(1)S=
(2)当S=1时,由 
,得1=
,
∴C=4或C=-4(舍去).
∴C=4,∴正方形边长为1cm.
(3)∵S=,∴欲使S≥4,需≥4,∴C2≥64.
∴C≥8或C≤-8(舍去),
∴C≥8.B卷答案:
一、
1.解:S=S梯形ABCD-S△EGD-S△EFA-S△BCF
=
×(3+6)×4-x(4-x)- x(6-x)-×4x
=x2-7x+18
∵
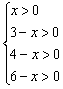
∴0<x<3,
故S=x2-7x+18(0<x<3).
2.解:
∵AB=4,AC=6,BC=2
∴AB2=(4)2 =48,AC2=62=36,BC2=(2)2=12.
∴AB2=AC2+BC2.
∴△ABC为直角三角形,且∠A=30°.
连结PB,则PB为⊙O的直径.
∴PD⊥AB.
∵在Rt△APD中,∠A=30°,PA=x,
∴PD=x,
∴y=PC2+PD2=(6-x)2+
=
-12x+36(0<x<6).
3.解:
(1)作PE⊥QR于E,
∵PQ=PR,∴QE=RE=QR=×8=4,PE=
=3,
当t=3时,QC=3,
设PQ 与DC相交于点G.
∵PE∥DC,∴△QCG∽△QEP,∴
,
∵S△QEP=×4×3=6,∴S=
(cm2)
(2)当t=5时,CR=3.
设PR与DC交于G,由△RCG∽△REP可求出S△RCG=
,
∴S=S△PBR-S△RCG=12-=
(cm2)
(3)当5≤t≤8时,如答图所示,QB=t-5,RC=8-t.
设PQ交AB于点H,由△QBH ∽△QEP,得S△QBH=
.
设PR交CD于G,由△PCG∽△REP,得S△RCG=
(8-t)2.
∴S=12--
=
即关系式为S=.
二、
4.解:(1)根据解答者的性别、年龄实事求是地代入即可.
(2)把p=120代入p=0.01x2+0.05x+107,得
120=0.01x2+0.05x+107.解得x1≈-39(舍去),x2=34.
故该女性的年龄大约为34岁.
(3)把p=130代入p=0.006x2-0.02x+120,得
130=0.006x2-0.02x+120.
解得x1≈-39(舍去),x2=43.
故该男性的年龄大约为43岁.
三、
5.解:∵PB=6-t,BE+EQ=6+t,
∴S=PB·BQ=PB·(BE+EQ)
= (6-t)(6+t)=-t2+18.
∴S=-t2+18(0≤t≤6).
6.解:若销售单价为x元,则每千克降低(70-x)元,日均多销售出2(70-x)千克,日均销售量为[60+2(70-x)]千克,每千克获利(x-30)元.依题意,得
y=(x-30)[60+2(70-x)]-500
=-2x2+260x-6500(30≤x≤70).
即y=-2x2+260x-6500(30≤x≤70).
7.解:由题意,得每件商品的销售利润为(x-30)元,那么m件的销售利润为y=m(x-30).
又∵m=162-3x,∴y=(x-30)(162-3x),
即y=-3x2+252x-4860.
∵x-30≥0,∴x≥30.
又∴m≥0,∴162-3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=-3x2+252x-4860(30≤x≤54).
8.解:(1)由图象可知,当x=600时,y=400;当x=700时,y=300,
代入y=kx+b中,得
解得k=-1,b=1000
∴y=-x+1000(500≤x≤800)
(2)销售总价=销售单价×销售量=xy,成本总价=成本单价×销售量=500y,
代入毛利润公式,得
S=xy-500y=x(-x+1000)-500(-x+1000)
=-x2+1500x-500000.
∴S=-x2+1500x-500000(500≤x≤800)
四、(一)
9.解:把x=3,y=15;x=-2,y=5分别代入y=ax2+(xm+c),
得
解得a=2,km+c=-3, ∴y=2x2-3.
(二)10.解:如答图,S矩形PNDM=xy,且2≤x≤4.
延长NP交EF于G,显然PG∥BF.
故
,即
,∴y=-x+5,
∴S=xy=-x2+5x,即S=-x2+5x(2≤x≤4).
五、11.解:(1)由矩形的一边长为x米,得另一边长为
米,即(6-x)米,
∴S=x(6-x)=-x2+6x,即S=-x2+6x,其中0<x<6.
(2)设此黄金矩形的长为x米,宽为y米,
则由题意,得
,解得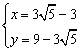
即当把矩形的长设计为
米时,矩形将成为黄金矩形,
此时S=xy=()(
)=
;
可获得的设计费为 ×1000≈8498(元).
12.解:(1)当t=5时,y=195,当t=25时,y=205.
∴讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中.
(2)当0<t≤10时,y=-t2+24t+100=-(t-12)2+244,
该图的对称轴为t=12, 在对称轴左侧,y随x的增大而增大,
所以,当t=10时,y有最大值240.
当10<t≤20时,y=240.
当20<t≤40时,y=-7t+380,y随x的增大而减小,
故此时y<240.
所以,当t=20时,y 有最大值240.
所以,讲课开始后10分钟时,学生的注意力最集中,能持续10分钟.
(3)当0<t≤10,令y=-t2+24t+100=180,
∴t=4.
当20<t≤40时,令=-7t+380=180,
∴t=28.57.
所以,老师可以经过适当安排,能在学生注意力达到所需的状态下讲解完这道题目.
二次函数C卷答案:
一、1.解:(1)y=20-
×1=-0.1x+30.
(2)z=y·x-40y-500-1500
=(30-0.1x)x-40(30-0.1x)-2000
=30x-0.1x2-1200+4x-2000
=-0.1x2+34x-3200.
(3)当x=160时,z=-0.1x2+34x-3200=-0.1×1602+34×160-3200=-320.
把z=- 320代入z=-0.1x2+34x-3200,
得-320=-0.1x2+34x-3200,x2-340x+28800=0,
∴(x-160) (x-180)=0.∴x=160或x=180.
当x=160时,y=-0.1x+30=-0.1×160+30=14(万件);
当x=180时,y=-0.1x+30=-0.1×180+30=12(万件).
二、
2.解:(1)∵OA=OB,AB=AC,∴△AOB和△ABC是等腰三角形.
∴∠B=∠BAO=∠C.∴△AOB∽△BAC.
∴
, 即 
,
∴y=
∵A为
上任意一点,BM≤AB≤BD,
而BM=
, BD=8,
∴
≤x≤8.
∴y= (≤x≤8).
(2)若OA⊥CA,则AC为⊙O的切线,即当OC2=OA2+AC2时,OA⊥CA,
∴(4+y)2=42+ x2,即y2+8y=x2.
由y=x2-8和y2+8y=x2两式可得y=4,
∴x=4,即当x=4时,CA是⊙O的切线.
(3)由(2)得x=4,CA是⊙O的切线,
此时y=4,
而OE=BE-OB=(8+4)-4=2,AE=
,
∴tan∠OAE=
.
3.解:
(1)过点A作AD⊥BC于D,则有AD=3×sin450=
.
设△MNC的MN边上的高为h,
∵MN∥BC,∴
.
∴h=
,
∴S=MN·h=
,
即S=
(0<x<4).
(2)若存在这样的线段MN,使S△MNC=2,则方程 =2必有实根,
即3x2-12x+16=0 必有实根.
但△=(-12)2-4×3×16=-48<0,说明此方程无实根,
所以不存在这样的线段MN.