上虞市2004学年第一学期初三期末试卷
数 学 卷
| 题 次 | 一 | 二 | 三 | 总 分 | ||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得 分 | ||||||||||
| 阅卷人 | ||||||||||
一、选择题（本题有12小题,每小题4分，共48分）
1、
化简的结果是（ ）
A． 2 B．—2 C．2或—2 D．4
2、下列各式中，属于最简二次根式的是（ ）
（A）
（B）
（C）
（D）
3、下列二次根式中，化简后与
被开方数相同的二次根式是（ ）
A． 
B．
C．
D．
4、以3和-1为两根的一元二次方程是（ ）
A.x2+2x-3=0 B.x2+2x+3=0 C.x2-2x-3=0 D.x2-2x+3=0
5、方程
的实数根是（ ）
（A）
（B）
，
（C）
（D）无实数根
6、已知
，那么
的值等于（
）
（A）
（B）
（C）
(D) 
7、在实数范围内将3x2-x-1分解因式，其结果是（ ）
A. 
B. 
C. 
D. 
8、关于二次函数y＝(x＋2)2－3的最大（小）值，叙述正确的是（ ）
（A）当x＝2时，有最大值－3 （B）当x＝－2时，有最大值－3
（C）当x＝2时，有最小值－3 （D）当x＝－2时，有最小值－3
9、将抛物线y=2x2向左平移1个单位,再向上平移3个单位得到的抛物线,其解析式是( )
(A)y=2(x+1)2+3 (B) y=2(x－1)2－3
(C) y=2(x+1)2－3 (D) y=2(x－1)2+3
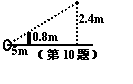10、小芳在打网球时，为使球恰好能过网（网高为0.8m），且落在对方区域离网5m的位置上，已知她击球的高度是2.4m，则她应站在离网的( )
（A）15m处 （B）10m处 （C）8m处 （D）7.5m处
11、若方程x2+(m+1)x+m+4=0两根的平方和为2，则m的值是（ ）
A. 3 B. –3 C. ±3 D. 3或-2
12、已知一个梯形被一条对角线分成两个相似三角形，如果两腰的比为1:4，那么两底的比为（ ）
A. 1:2 B. 1:4 C. 1:8 D. 1:16
二、填空题（本题有6小题，每小题5分，共30分）
13、已知在正方形ABCD中，F是AD的中点，BF与AC交于点G，则△AFG与△BGC的面积之比是___________．
14、若a、b是方程x2-3x+1=0的两个根，则
的值为
．
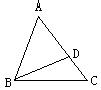
15、如图，已知点D是△ABC中AC边上的一个点，要使△ABD与原三角形相似，请你添加一个条件为_________________________．
16、已知：抛物线在直角坐标系中的位置如图所示，则抛物线的对称轴是 ；
17、直角三角形ABC中，
度，CD⊥AB于D，CD=，AD=1，则BD的长是
；
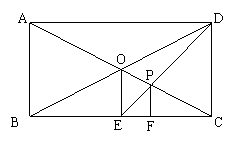18、在矩形ABCD中，对角线AC、BD相交于点O，过点
O作OE⊥BC，垂足为E，连结DE交A于点P，过P作
PF⊥BC，垂足为F，则
的值是_____.
三、解答题（本题有7小题，共72分）下列各小题都必须写出解答过程
19、(本题6分)计算：
20、（本题10分）解方程（组）：
(1) 
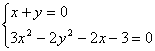（2）
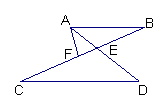21、(本题10分)如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
求证：(1) ∠EAF=∠B； (2)AF2=FE·FB
22、（本题10分）已知一抛物线与x轴的交点是A（-1，0）、B（m，0），又经过第四象限的点C（1，n），且m+n= -1，mn= -12，求此抛物线的解析式．
23、（本题10分）如图，E是△ABC外接圆上一点，AE交BC于D，且AB:BD=AE:EC.
(1)求证：BE=______（先填后证）；
(2)若AB=6cm，AC=8cm，BC=10cm，求BE的长.
24、（本题12分）为了测量校园内一棵不可攀登的樟树的高度，学校数学应用实践小组做了如下的探索：
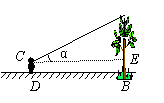
实践一：根据《自然科学》中的反射定律，利用一面镜子和一根皮尺，设计如右示意图的测量方案：把镜子放在离樟树（AB）8.7米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.7米，观察者目高CD=1.6米，请你计算樟树（AB）的高度．（要求：写出必要的说理过程，最终结果精确到0.1米）
实践二：提供选用的测量工具有：①皮尺一根；②教学用三角板一副；③长为2.5米的标杆一根；④高度为1.5米的测角仪（能测量仰角、俯角的仪器）一架。请根据你所设计的测量方案，回答下列问题：
（1）在你设计的方案中，选用的测量工具是（用工
具的序号填写）
（2）在右图中画出你的测量方案示意图；
（3）你需要测得示意图中的哪些数据，并分别用a、b、c、α等表示测得的数据：
（4）写出求樟树高的算式：AB= ．
25、（本题14分）我市“利必好”公司生产的A种产品，它的成本是2元，售价是3元，年销售量为100万件，为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x（十万元）时，产品的年销售量将是原销售量的y倍，且y是x的二次函数，它们的关系如右表：
（1）求y与x的函数关系式；
（2）如果把利润看作是销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费x（十万元）的函数关系式：
（3）如果投入的年广告费为10~30万元，问广告费在什么范围内，公司获得的年利润随广告费的增大而增大？
数学卷参考答案及评分意见
一、 选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | B | C | C | A | D | D | A | B | B | D |
二、填空题
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 | 1:4 | 5 | 略 | 直线 | 3 |
|
三、 解答题
19、(本题6分)解：原式=
（第一项1分，后两项各2分）=-1（6分）
20、(本题10分)（1）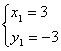
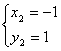（5分）
（2）解出 x=2，x=5（3分），检验后得x=2（5分）
21、(本题10分) (1)∵AB∥CD,∴∠B=∠C (2分) 又∵∠EAF=∠C,∴∠EAF=∠B (4分)
(2)在⊿AFB与⊿EFA中,∵∠EAF=∠B,∠AFB=∠EFA,∴⊿AFB=∽⊿EFA (7分)
∴
,即AF2=FE·FB (10分)
22、（本题10分）由m+n=
-1，mn= -12，知m、n是方程
的两个根，故可得两根为3和-4
(4分) ，因点C（1，n）经过第四象限，知n＜0，所以m=3，n=-4 (7分) ，从而抛物线与x轴的交点是A（-1，0）、B（3，0），设
，点C（1，-4）代入，得
(9分)，因此抛物线的解析式为
．(10分)
23、（本题10分）（1）BE=EC（2分）
AB:BD=AE:EC且∠ABD=∠AEC 
△ABD∽△AEC（4分）
∠BAD=∠EAC 
（6分）
（2）由AB=6，AC=8，BC=10得BC2=AC2+AB2∠BAC=90°（8分）
∠BEC=90°，BE=CE 2BE2=100BE=
（10分）
24、（本题12分）解：实践一：由题意知 ∠CED=∠AEB，∠CDE=∠ABE=Rt∠
∴△CED∽△AEB ……………………3分
∴
∴
∴AB≈5.2米（6分，只有计算式子只给3分）
实践二：
方案（一）（1）①② ；(7分)
（2）示意图如右；（9分）
（3）CD=a,BD=b；（10分）
（4）AB= a＋b；（12分）
(注：取∠ACE=60°或30°时，则相应给分)
方案（二）（1）①③；(7分)
（2）示意图如右；（9分）
|
（4）AB=
（12分）
方案（三）（1）①④；(7分)
（2）示意图如右；（9分）
（3）BD=a，∠ACE=α；（10分）
（4）AB=a·tgα＋1.5（12分）
(注：本题有其它测量方案，只要方法合理，则相应给分)
25、（本题14分）（1）设y=ax2+bx+c（1分）
由题意得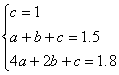
（4分） 得
（7分）所以y=-0.1x2+0.6x+1（8分）
(2)s=
（11分）
（3）因为
，而 a=-1<0，所以当在对称轴直线
的左侧时，S随X的增大而增大，即当广告费用在10~25万时公司获得的年利润随广告费的增大而增大． （14分）