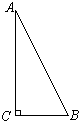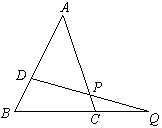初三数学试卷(一)
第Ⅰ卷(选择题)
一、下列各题均有四个选项,其中只有一个是正确的。
1、用科学记数法表示199900正确的是
A.1999×102 B.199.9×103
|
|
C.19.99×104 D.1.999×105
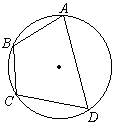
2、如图,已知圆周角![]() 那么圆周角
那么圆周角![]() 的度数为
的度数为
A.130° B.100°
C.50° D.40°
3、不等式组![]() 的解集是
的解集是
A.![]() B.
B.![]() C.
C.![]() D.无解
D.无解
4、计算:![]() 的结果是
的结果是
A.8 B.4 C.0 D.-4
5、下列因式分解正确的是
A.![]()
B.![]()
C.![]()
D.![]()
6、某校在学军活动中,一学生连续打靶5次,命中的环数如下:0,2,5,2,7这组数据的中位数与众数分别是(单位:环)
A.2,2 B.5,2 C.5, 7 D.2,7
7、方程![]() 的根为
的根为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8、下列命题中,正确的命题是
A.一组对边平行但不相等的四边形是梯形
B.圆的内接平行四边形是正方形
C.有一个角相等的两个等腰三角形相似
D.一组对边相等,另一组对边平行的四边形是平行四边形
9、在⊙O中,弦AB和CD相交于P,且AB^CD,如果AP=4,PB=4,CP=2,那么⊙O的直径为
A.4 B.5 C.8 D.10
10、函数![]() 中,自变量x的取值范围是
中,自变量x的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11、已知:⊙O1的半径为2cm,⊙O2的半径为5cm,并且⊙O1与⊙O2相切,则这两个圆的圆心距为
A.3cm B.7cm C.9cm D.3cm或7cm
12、二次函数![]() 的图象的顶点坐标是
的图象的顶点坐标是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
|
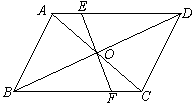
13、如图,四边形ABCD是平行四边形,对角线AC与BD交于O点,直线EF过O点,光AD于E,交BC于F,则图中的全等三角形共有
A.7对 B.6对
C.5对 D.4对
14、关于x的方程![]() 中,如果
中,如果 ![]() ,那么根的情况是
,那么根的情况是
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.不能确定
15、在![]() 中,CD是斜边AB上的高,已知
中,CD是斜边AB上的高,已知![]() 那么
那么![]() 的值是
的值是
A.![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
16、圆锥的高为![]() ,底面积半径为2,则该圆锥侧面展开图的面积是
,底面积半径为2,则该圆锥侧面展开图的面积是
A.![]() B.6
B.6 ![]() C.2
C.2 ![]() D.
D. ![]()
17、如果一个正多边形的一个内角是135°,则这个正多边形是
A.正八边形 B.正九边形 C.正七边形 D.正十边形
|
|
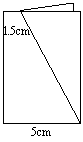
18、如图,把长为10cm的长方形纸片对折以后,按图中的虚线剪出一个梯形并打开,则打开后的梯形中位线长为
A.3.25cm B.6.5cm
C.3.5cm D.13cm
19 、已知![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上,则直线
的图象上,则直线![]() 不经过的象限为
不经过的象限为
A.第一象限 B.第二象限 C.第三象限 D.第辊象限
|
|
20、如图,在![]() 中,
中,![]()
![]() ,
,
动点P从点C出发,以每秒2cm的速度沿CA、AB运动到点B,当使![]() 时,则P点从C点出发后经过了
时,则P点从C点出发后经过了
A.1秒 B.7.75秒
C.1秒或7.75秒 D.3秒
第Ⅱ卷(解答题)
二、计算:
![]()
三、解方程:
![]()
四、列方程解应用题
某乡村计划用若干时间种55棵果树,开始按原计划种树1小时30分钟后,加快了速度,比原计划每小时多种5棵果树,结果不但比原计划少用了1小时,而且多种了5棵果树,问原计划每小时种多少棵果树?
|
|
五、
已知:如图,在![]() 中,D为AB边上一点,Q为BC延长线上一点,DQ交AC于P,且
中,D为AB边上一点,Q为BC延长线上一点,DQ交AC于P,且![]() 。
。
求证:![]()
六、
|
|
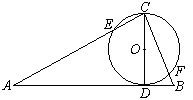
已知:如图,在![]() 中,若边长AC、BC是关于x的方程,
中,若边长AC、BC是关于x的方程,![]() 的两个根,且
的两个根,且![]() 于D,以CD为直径作圆,分别交AC、BC于E、F。
于D,以CD为直径作圆,分别交AC、BC于E、F。
(1)判断![]() 的形状,并求
的形状,并求![]() 三边的长;
三边的长;
(2)求![]() 的值;
的值;
(3)求AE的长。
七、
|
|
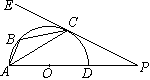
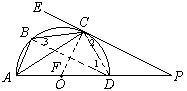
已知:如图, ![]() 内接于以AD为直径的半圆O,PE与半圆O相切,切点为C,AD的延长线与PE相交于点P,
内接于以AD为直径的半圆O,PE与半圆O相切,切点为C,AD的延长线与PE相交于点P,![]() ,若
,若![]() ,求四边形PABC的面积和
,求四边形PABC的面积和![]() 的另外两边的长。
的另外两边的长。
八、
|
|
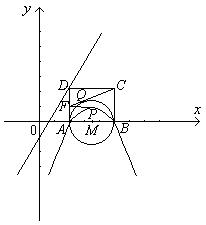
已知:矩形ABCD(字母顺序如图)的边长![]() ,将此矩形放在平面直角坐标系xoy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线
,将此矩形放在平面直角坐标系xoy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线![]() 经过这两个顶点中的一个顶点。
经过这两个顶点中的一个顶点。
(1)求出矩形的顶点A、B、C、D的坐标;
(2)以AB为直径作⊙M,经过A、B两点的抛物线![]() 的顶点是
的顶点是![]() 点,
点,
①若点P同时在⊙M和矩形ABCD内部,求a的取值范围;
②过点C作⊙M的切线交AD于F点,,当PF∥AB时,判断抛物线与y轴的交点是否在直线![]() 上,并说明理由。
上,并说明理由。
【参考答案】:
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | D | C | A | A | C | A | D | B |
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | D | B | B | B | A | B | A | B | C | C |
二、计算:
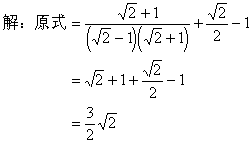
三、解方程:
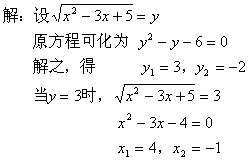
当![]() ,根据算术根的定义,
,根据算术根的定义,![]() 不可能是负数,所以方程无解。
不可能是负数,所以方程无解。
经检验,![]() 都是原方程的解
都是原方程的解
∴原方程的解为![]()
四、列方程解应用题:
解:设原计划每小时种x棵果树
根据题意,得![]()
整理,得 ![]()
解这个方程,得![]() (舍)
(舍)
经检验:![]() 是原方程的根。
是原方程的根。
答:原计划每小时种10棵果树。
五、
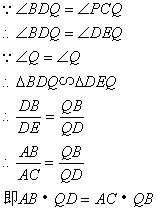
证明:过D作DE∥AC交BC于E。
则![]()
六、
解:(1)∵AC、BC是关于x的方程![]() 的两个根。
的两个根。

设BC=3m,则AB=5m,AC=4m
代入①,得 ![]()
解得 m=2
∴BC=6,AC=8,AB=10
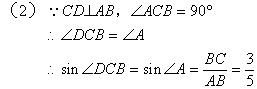
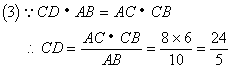
Rt![]()
∵CD是⊙O的直径,且CD⊥AB,
∴AD 是⊙O的的切线。
由切割线定理![]()
∴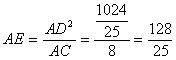
七、
解:连结CD、BD、CO。设BD与CO交于F。
|
|
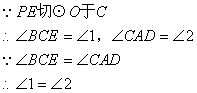
![]()
∴BD∥PE
∴∠P=∠BDA
∵AD是![]() 的直径,
的直径,
∴∠ABD=90°
∴tg∠BDA=![]()
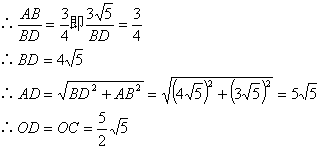
∵PE切![]() 于C
于C
∴OC⊥PE。
在Rt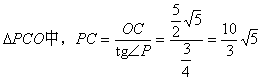
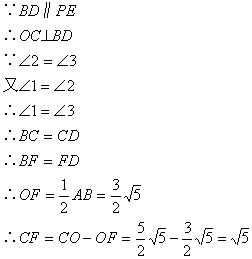
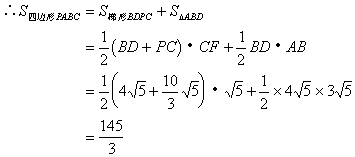

![]()
|
|
八、
解:(1)![]()
设A![]()
![]()
①若直线过C点,则![]()
![]()
②若直线过D点,则![]()
![]()
![]()
(2)①∵抛物线![]()
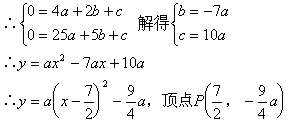
∵点P同时在⊙M和矩形ABCD内部,
∴![]()
解得![]()
②如图,设切线CF与⊙M的切点Q,AF=n,易知AD,BC都是⊙M的切线。
∴![]()
在Rt![]() 中
中
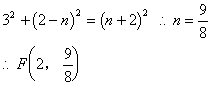
∴当PF∥AB时,P点纵坐标为![]()
∴![]()
∴抛物线的解析式为![]()
抛物线与y轴的交点坐标为(0,-5),将其代入![]() 中
中
左=-5,右=-1
∵左边![]() 或边
或边
∴抛物线与与y轴的交点不在直线![]() 上。
上。