长沙市2005年初中毕业会考试卷
数 学
(试验区)
考生注意:本试卷共26道小题,时量120分钟,满分120分.
| 得分 | 评卷人 | 复评人 |
一、填空题(本题共8个小题,每小题3分,满分24分)
1.![]() 的相反数是 .
的相反数是 .
2.因式分解:![]() = .
= .
 3.据《中华人民共和国2004年国民经济和社会发展统计公报》发布的数据,2004年我国因洪涝和干旱造成的直接经济损失达97 500 000 000元,用科学记数法表示这一数据为
元.
3.据《中华人民共和国2004年国民经济和社会发展统计公报》发布的数据,2004年我国因洪涝和干旱造成的直接经济损失达97 500 000 000元,用科学记数法表示这一数据为
元.
4.在△![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() .
.
 5.甲、乙两人进行射击比赛,在相同条件下各射击10次.他们的平均成绩均为7环,10次射击成绩的方差分别是:
5.甲、乙两人进行射击比赛,在相同条件下各射击10次.他们的平均成绩均为7环,10次射击成绩的方差分别是:![]() ,
,![]() .成绩较为稳定的是 .
.成绩较为稳定的是 .
(填“甲”或“乙”).
6.方程![]() 的解是 .
的解是 .
7.如图,![]() 要使△
要使△![]() △
△![]() ,应添加的条件
,应添加的条件
是 (添加一个条件即可).
8.请在图中作出△![]() 的角平分线
的角平分线![]() (要求保留作图痕迹).
(要求保留作图痕迹).
| 得分 | 评卷人 | 复评人 |
二、选择题(本题共8个小题,每小题3分,满分24分)
请将你认为正确的选择支的代号填在下面的表格里
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
9.已知![]() ,
,![]() 两数在数轴上对应的点如图所示,下列结论正确的是
两数在数轴上对应的点如图所示,下列结论正确的是
 A、
A、![]() . B、
. B、![]() .
.
C、![]() . D、
. D、![]() .
.
10.下列运算正确的是
A、![]() . B、
. B、![]() .
.
C、![]() . D、
. D、![]() .
.
11.下列图形中,不是正方体的展开图的是
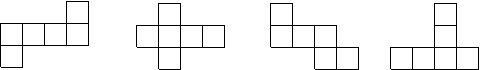 |
A B C D
12.不等式组![]() 的解集为
的解集为
A、![]() . B、
. B、![]() . C、
. C、![]() . D、无解.
. D、无解.
13.已知矩形的面积为10,则它的长![]() 与宽
与宽![]() 之间的关系用图象大致可表示为
之间的关系用图象大致可表示为
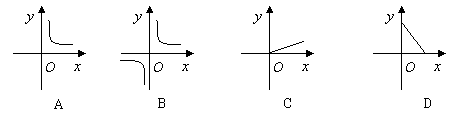 |
14.下列说法正确的是
A、等腰梯形既是中心对称图形又是轴对称图形.
B、正方形的对角线互相垂直平分且相等.
C、矩形是轴对称图形且有四条对称轴.
D、菱形的对角线相等.
15.下图所示的几何体的俯视图是
 |
16.下列事件,是必然事件的是
A、掷一枚均匀的骰子,骰子停止后朝上的点数是6.
B、打开电视,任意选择一个频道,正在播新闻.
C、在地球上,抛出去的篮球会下落.
D、随机地从0,1,2,![]() ,
,![]() 这十个数中选取两个数,和为20.
这十个数中选取两个数,和为20.
| 得分 | 评卷人 | 复评人 |
三、解答题(本题共6个小题,每小题6分,满分36分)
17.计算:![]() .
.
18.先化简,再求值:
![]() ,其中
,其中![]() ,
,![]() .
.
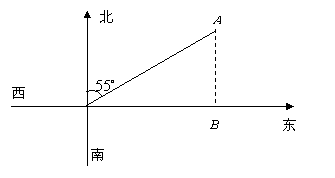
19.如图,灯塔![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 方向上,
方向上,
且与港口的距离为80海里.一艘船上午9时从港
口![]() 出发向正东方向航行,上午11时到达
出发向正东方向航行,上午11时到达![]() 处,
处,
|
(精确到![]() 海里/小时).
海里/小时).
(供选用数据:![]() ,
,
![]() ,
,![]() )
)
20.某校学生会在“暑假社会实践”活动中组织学生进行了社会调查,并组织评委会对学生写出的调查报告进行了评比.学生会随机抽取了部分评比后的调查报告进行统计,绘制了统计图如下,请根据该图回答下列问题:
(1)学生会共抽取了 份调查报告;
(2)若等第![]() 为优秀,则优秀率为 ;
为优秀,则优秀率为 ;
(3)学生会共收到调查报告1000份,请估计该校有多少份调查报告的等第为![]() ?
?
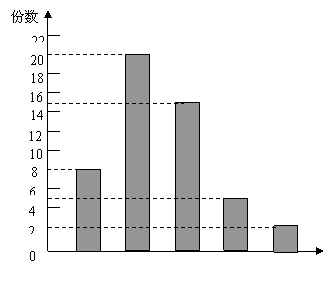 |
A B C D E 等第
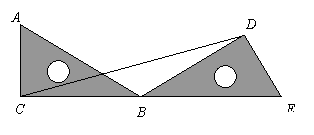
21.如图所示,把一个直角三角尺![]() 绕着
绕着![]() 角的顶点
角的顶点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 与
与![]() 的延长线上的点
的延长线上的点![]() 重合.
重合.
(1)三角尺旋转了多少度?
(2)连结![]() ,试判断△
,试判断△![]() 的形状;
的形状;
(3)求![]() 的度数.
的度数.
 |
22.一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色以外没有任何区别.
(1)小王通过大量反复的实验(每次取一个球,放回搅匀后再取第二个)发现,取出黑球的频率稳定在![]() 左右,请你估计袋中黑球的个数;
左右,请你估计袋中黑球的个数;
(2)若小王取出的第一个球是白球,将它放在桌上,闭上眼睛从袋中余下的球中再任意取一个球,取出红球的概率是多少?
四、解答题(本题共2个小题,每小题8分,满分16分)
| 得分 | 评卷人 | 复评人 |
23.(本题满分8分)
某工厂第一季度生产甲、乙两种机器共480台.改进生产技术后,计划第二季度生产这两种机器共554台,其中甲种机器产量要比第一季度增产10%,乙种机器产量要比第一季度增产20%.该厂第一季度生产甲、乙两种机器各多少台?
 |
| 得分 | 评卷人 | 复评人 |
24.(本题满分8分)
已知点![]() 、
、![]() 在△
在△![]() 的边
的边![]() 所在的直线上,且
所在的直线上,且![]() ,
,![]() ,
,![]() 、
、![]() 分别交边
分别交边![]() 所在的直线于点
所在的直线于点![]() 、
、![]() .
.
(1)如图1,如果点![]() 、
、![]() 在边
在边![]() 上,那么
上,那么![]() ;
;
(2)如图2,如果点![]() 在边
在边![]() 上,点
上,点![]() 在
在![]() 的延长线上,那么线段
的延长线上,那么线段![]() 、
、![]() 、
、![]() 的长度关系是 ;
的长度关系是 ;
(3)如图3,如果点![]() 在
在![]() 的反向延长线上,点
的反向延长线上,点![]() 在
在![]() 的延长线上,那么线段
的延长线上,那么线段![]() 、
、![]() 、
、![]() 的长度关系是 .
的长度关系是 .
对(1)(2)(3)三种情况的结论,请任选一个给予证明.

五、解答题(本题共2个小题,每小题10分,满分20分)
| 得分 | 评卷人 | 复评人 |
 25.(本题满分10分)
25.(本题满分10分)
某通讯器材公司销售一种市场需求较大的新型通讯产品.
已知每件产品的进价为40元,每年销售该种产品的总开支
(不含进价)总计120万元.在销售过程中发现,年销售量
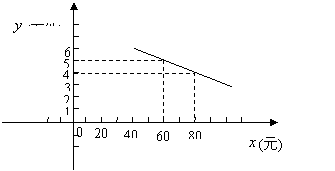
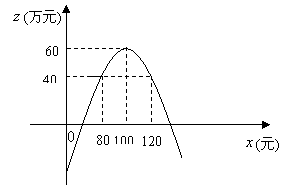
![]() (万件)与销售单位
(万件)与销售单位![]() (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试写出该公司销售该种产品的年获利![]() (万元)关于销售单价
(万元)关于销售单价![]() (元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价
(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价![]() 为何值时,年获利最大?并求这个最大值;
为何值时,年获利最大?并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
 |
| 得分 | 评卷人 | 复评人 |
26.(本题满分10分)
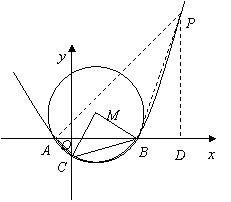
已知抛物线![]() 经过点
经过点![]() 、
、![]() (
(![]() ),且与
),且与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 、
、![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
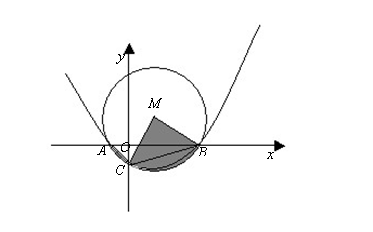
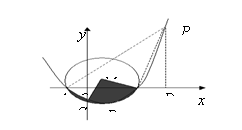
(2)如图所示,![]() 过
过![]() 、
、![]() 、
、![]() 三点,求阴影部分扇形的面积
三点,求阴影部分扇形的面积![]() (用含
(用含![]() 的式子表示);
的式子表示);
(3)在![]() 轴上方,若抛物线上存在点
轴上方,若抛物线上存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,求
相似,求![]() 的值.
的值.
 |
长沙市2005年初中毕业会考数学参考答案及评分标准(实验区)
一、填空题(每小题3分,满分24分)
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]()
5.乙 6.![]() 7.
7.![]() 等 8.略
等 8.略
二、选择题(每小题3分,满分24分)
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | A | C | D | C | A | B | B | C |
三、解答题(每小题6分,满分36分)
17.解:原式![]() .········································································ (6分)
.········································································ (6分)
18.解:原式=![]() .··················································· (4分)
.··················································· (4分)
当![]() ,
,![]() 时,原式
时,原式![]() .··············································· (6分)
.··············································· (6分)
19.解:连结![]() ,由题意得:
,由题意得:![]() ,
,![]() ,
,![]()
在Rt△![]() 中,
中,![]() ,
,![]() ,···· (5分)
,···· (5分)
![]() .答:略.································· (6分)
.答:略.································· (6分)
20.(1)50;(2分) (2)16%(4分) (3)![]() 份···· (6分)
份···· (6分)
21.(1)![]() ; (2)等腰三角形; (3)
; (2)等腰三角形; (3)![]() .(每小题2分,共6分)
.(每小题2分,共6分)
22.(1)5个;································································································· (3分)
(2)![]() .·································································································· (6分)
.·································································································· (6分)
23.解:设该厂第一季度生产甲种机器![]() 台,乙种机器
台,乙种机器![]() 台,依题意得;·········· (1分)
台,依题意得;·········· (1分)
![]()
 ······ (5分)
······ (5分)
解得:![]() ························································································· (7分)
························································································· (7分)
答:该厂第一季度生产甲种机器220台,乙种机器260台.························· (8分)
24.(2)线段![]() 、
、![]() 、
、![]() 的长度的关系为:
的长度的关系为:![]() .············ (2分)
.············ (2分)
(3)线段![]() 、
、![]() 、
、![]() 的长度的关系为:
的长度的关系为:![]() .·············· (4分)
.·············· (4分)
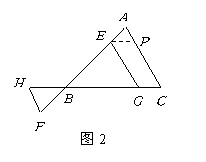 证明(2):如图2,过点
证明(2):如图2,过点![]() 作
作![]() 交
交![]() 于
于![]() ·································· (5分)
·································· (5分)
![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]()
![]()
![]()
![]()
![]() ,
,![]()
又![]()
![]() △
△![]() △
△![]() ·················· (7分)
·················· (7分)
![]()
![]()
即![]() ····················································· (8分)
····················································· (8分)
(用平行线分线段成比例或相似三角形的性质等证明均参照以上标准记分)
25.解:(1)设![]() ,它过点
,它过点![]()
![]() 解得:
解得: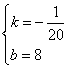 ···························································· (2分)
···························································· (2分)
![]() .············································································· (3分)
.············································································· (3分)
(2)![]()
![]() 当
当![]() 元时,最大年获利为60万元.········································· (6分)
元时,最大年获利为60万元.········································· (6分)
 (3)令
(3)令![]() ,得
,得![]() ,
,
整理得:![]()
解得:![]() ,
,![]() ················· (8分)
················· (8分)
由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.
························································· (9分)
又因为销售单价越低,销售量越大,所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.·················································· (10分)
26.(1)依题意得有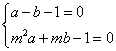 ,解得:
,解得:  ·············· (2分)
·············· (2分)
![]() 抛物线的解析式为:
抛物线的解析式为:![]()
(2)![]() 时,
时,![]()
![]()
![]()
![]() ,
, ![]()
![]()
又![]()
![]() .······································· (5分)
.······································· (5分)
(3)如图,由抛物线的对称性可知,若抛物线上存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,则
相似,则![]() 关于对称轴的对称点
关于对称轴的对称点![]() 也符合题意,即
也符合题意,即![]() 、
、![]() 对应的
对应的![]() 值相同.下面以点
值相同.下面以点![]() 在对称轴右侧进行分析: (6分)
在对称轴右侧进行分析: (6分)
情形一:如图,△![]()
![]() △
△![]()
则![]() ,
,![]()
过![]() 作
作![]() 轴垂足为
轴垂足为![]() ,连
,连![]() 、
、![]() .
.
在Rt△![]() 中
中 ![]()
![]() ,
,![]() 可令
可令![]()
若![]() 在抛物线上,
在抛物线上,
则有![]()
即![]() ,解得
,解得![]() ,
,![]()
![]() ,
,![]() 显然
显然![]() 不合题意,舍去.
不合题意,舍去.
此时![]() ①
①
又由![]() ,得
,得![]() ②
②
由①、②有:![]() .
.
整理得:![]()
解得:![]() ,
, ![]()
![]()
即若抛物线上存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,
相似,
 则
则![]() ; ····································································· (8分)
; ····································································· (8分)
情形二:△![]() △
△![]()
则![]() ,
,![]()
同于情形一:![]()
![]() ,
,
![]() 可令
可令![]()
若![]() 在抛物线上则有
在抛物线上则有![]()
整理得:![]() 解得:
解得:![]() ,
,![]()
![]() 或
或![]() 显然
显然![]() 不合题意,舍去!
不合题意,舍去!
此时![]() ①
①
又由![]() 得:
得:![]() ②
②
由①、②得: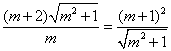
整理得![]() ,显然无解!······································································· (10分)
,显然无解!······································································· (10分)
综合情形一、二得:若抛物线上存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,则
相似,则![]() .
.
(特别说明:学生只考虑一种情形时,缺情形一,扣2分;缺情形二,扣1分)