初 三 年 级 阶 段 考 试
数 学 试 卷
命题单位：黄陂区罗汉中学 时间：120分钟
| 题号 | 一 | 二 | 三 | 四 | 总分 |
| 得分 |
一、 选择题（每小题3分，共36分）
1. 点P 在第二象限，且P点到x轴的距离为3, 到y轴的距离为2, 则P点坐标为（ ）
A （2, -3） B （3, -2） C （－2, 3） D （－3, 2）
2. 若点A（x,-3）和点B（12, y）关于原点对称，则x+y的值为（ ）
A 9 B －9 C －15 D 15
3. 已知圆的直径是13cm，如果直线和圆心的距离为6.5cm，那么直线与圆的位置关系为（ ）
A 相交 B 相切 C 相离 D 不能确定
4.
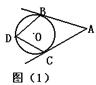已知如图（1）AB CD分别切⊙O于B、C两点，点D 是⊙O上一点，∠D＝400，则∠A的度数为（
）
A 1400 B 1200 C 1000 D 800
5.
如图（2），已知∠AOB=300，M为OB上一点，且OM＝5cm, 以M为圆心r为半径与直线OA有且只有一个交点的圆的半径r长为（ ）
A 2cm B 3cm C .52cm D 3.5cm
6. 直线y＝1/2x+2与主轴的交战坐标为（ ）
A （0, 2） B （2, 0） C （－4, 0） D （0, -4）
7. 已知一次函数y=kx-2，如果y随x的增大而减小，则它的图像经过（ ）
A第二、三、四象限
B 第一、二、三象限
C 第一、三、四象限 D 第一、二、三象限
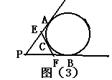
8. 如图（3），P 为⊙O外一点，PA PB切⊙O于A、B，PA=PB=4cm，EF切⊙O于C交PA PB于E、F，则△PEF的周长等于（ ）
A 4cm B 8cm C 12cm D 16cm
9.
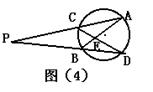如图（4），⊙O的两条弦AB、CD相交于点E，AC和BD的延长线交于点P，下列结论成立的是（ ）
A PB·PD=PC·PA B PC·AC=PB·BD
C CE·AE=BE·ED D CE·CD=BE·BA
10. 
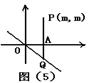已知函数y=kx的图象如图（5）所示，过点P(m,
m)，平行y轴的直线交x轴于A，交函数y=kx的图象于点Q，若线段AP>AQ，则kx的取值范围（ ）
A k>0 B k<0 C -1<k<0 D k<-1
11. 
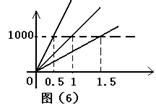ABC三种物质的质量与体积关系如图（6）所示：（ρ表示物质密度）由图可知下列关系正确的是（ ）
A ρA>ρB>ρA>ρc,且ρC> ρ水
B ρA>ρB>ρA>ρc,且ρA> ρ水
C ρA<ρB<ρA<ρc,且ρC> ρ水
D ρA<ρB<ρA<ρc,且ρA> ρ水
12. 
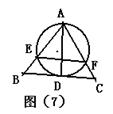如图（7）在△ABC中，AD是角平分线，⊙O过点A与BC切于点
D，与AB、AC分别交于E、F，下列结论：（1）DE=DF（2）AD2=AB·AC（3）S△ABC＝S△ACD（4）
＝
， 其中不正确的是（ ）
A ① ② ③ B ① ④ C ② ③ ④ D ① ③ ④
二、
填空题（每小题3分，共12分）
13.一条直线经过A(0, 1)，B(-1/2, 0)则其解析式为
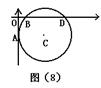
14.如图（8）在直角坐标系中，⊙C与y轴相切与x轴相交于（1, 0），（5, 0）两点，圆心C在第四象限，则C点坐标为（
）
15.点P不在⊙O上，过P的直线交⊙O于AB，若PA.PB=24，OP=5，则⊙O的半径长为
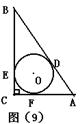
16.如图（9），在Rt△ABC中，⊙O分别切AB、BC、AC于D、E、F三点，AB=10，∠A的余弦值为3/5，则S⊙O=
三、解答题（17、18小题各8分，19、20小题各10分，21小题12分）
17.直线y＝3x+b和两坐标轴成三角形的面积等于24，求b
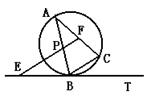
18. 已知△ABC是⊙O的内接三角形，BT为⊙O切线，B为切点，P为直线AB上的一点，过P 作BC的平行线交直线BT于E，交直线AC于F，
（1） 当P在线段AB上时，求证：PA·PB=PE·PF
（2） 点P在线段BA的延长线上时，第（1）题 的结论还成立吗？如果成立，请画图证明；如果不成立，请说明理由。
19.一次函数y＝
的图象分别与x轴y轴交于A、B，设有点C（a，0），且a<0有△ABC为等腰三角形，求经过B 、C两点的直线的解析式。
20. PA为⊙O的切线，A为切点，PBC为割线，∠APC的平分线PF交AC于F，交AB于E。
（1） 求证：AE=AF
（2）
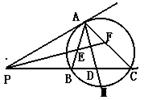若PB:PA=1:2，M是BC上的点，AM交BC于D，PD＝DC，试确定M点在BC上的位置，并证明你的结论。
21. 某童装厂现有甲种布料38米，乙种布料26米，现计划用这两种布料生产L、M两种型号的童装共50套，已知做一套L型号的童装需用甲种布料0.5米，乙种布料1米，可获利45元；做一套M型号的童装需用甲种布料0.9米，乙种布料0.2米，可获利30元，设生产L型号的童装套数为x，用这批布料生产这两种型号的童装所获利润为y（元）。
（1）写出y关于x的函数解析式，并求出自变量x’的取值范围。
（2）该厂在生产这批童装中，当L型号的童装为多少套时，能使该厂所获的利润最大？最大利润是多少？
四、综合题（每小题12分）
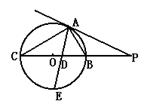
22.△ABC的内接三角形，AC>AB，BC为⊙O的直径，P为AB延长线上的点，且PA2＝PB·PC，∠BAC的平分线交BC于D，交⊙O于E，
（1） 求证：PA是⊙O的切线
（2） 若⊙O的直径为10，且AD、AE是方程x2－mx+48=0的两根，求tan∠PAB值
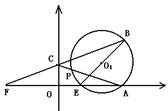
23.在直角坐标中，A在x轴正半轴上，OA＝4，B(4,4)，点E从0出发沿x轴正半轴运动，点F从0点出发，沿x轴负半轴运动，以BE为直径作⊙O1，BF与y轴交于C。
（1）若E以1个单位/秒，点F以4单位/秒的速度同时出发，问经过几秒钟，⊙O1与y轴相切于C点？
（2）若E以1个单位/秒，点F以m单位/秒的速度同时出发，E在OA内运动，经过2秒钟，直线CE与⊙O1相切，试求直线BC的解析式，并求点F的速度。
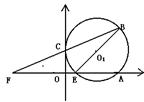（3）若E、F两点同时出发，点E以1个单位/秒，点F以恰当的速度运动，保持OE＝OC，点E在OA内，连AC交⊙O1于P ，试问AP·AC的值是否发生变化？若不变，请说明理由并求值，若变化，说明变化范围？