| 初二几何---解直角三角形 |
|
|
| 一.选择题 (本大题共 24 分) |
| 1. Rt△ABC 中,CD为斜边AB上的高,CD=2,BD=8,则tgA的值是 ( ) (A)2 (B)4 (C) |
| 2. 在△ABC 中,∠C=90° ,在下列关系式 (1)a=c·sinA,(2)b=a·ctgB,(3)a=b·tgA,(4)b=c·cosB,(5) (A)3个 (B)4个 (C)5个 (D)6个 |
| 3. 下列结论中正确的是( ) (A)sin30º+sin40º=sin70º (B)cos60º+cos30º=cos30º (C)2ctg30º=ctg60º (D)sin245º+cos245º=1 |
| 4. 等腰三角形底边上的高等于腰的一半,则顶角为( ) (A)30º (B)60º (C)90º (D)120º |
| 5. 已知cos44º30'=0.7133º2'的修正值是0.0002,则cos44º32'的值是 ( ) (A)0.7131 (B)0.7135 (C)0.7133 (D)-0.7131 |
| 6. 在Rt△ABC 中, ∠C=90° ,如果sinA= |
| 7. 在 Rt△ABC 中,若 (A)30º (B)45º (C)60º (D)75º |
| 8. 两灯塔A和B与海岸上观测站C的距离相等。如果A在C的北偏东40º,B在C南偏东60º,那么A在B的( ). (A)北偏东10º (B)南偏东20º (C)北偏西10º (D)南偏西20º |
| 9. 化简 (A)ctg50º-tg50º (B)tg50º-ctg50º (C)ctg50º-tg50º- |
| 10. 如果tgα是方程x2-4x+3=0的一个根,那么锐角α的正弦值是( ) (A) (C) |
| 11. 菱形ABCD的对角线 AC=10cm,BD=6cm,那么 (A) |
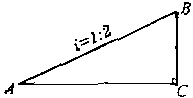
| 12. 由图中所给数据,则BC:CA:AB= ( )
(A)1:2:5 (B)1:√3 :2 (C)1:2: √5 (D)1:√3:√5 |
| 二.填空题 (本大题共 40 分) |
| 1. 在△ABC中,∠C=90° , ∠A=60° , AC=4√3 , 则BC= ,AB= . |
| 2. 设a为锐角,且tgα是方程x2+2x-3=0的根,那么sin2α+6sinα-½ctgα=_______。 |
| 3. 在△ABC 中,∠C=90° ,a+b+c=48, |
| 4. 在△ABC 中, ∠C=90° ,AB=13,BC=5, 则sinA= ______ ,cosA=_____ ,tgA= _____ _ ,ctgA=_____ . |
| 5. 在△ABC中, ∠C=90° , BC=√3 , AB=2√3 ,AC= , ∠A= , ∠B= . |
| 6. sin235º+sin255º=________;tg25º × tg65º=________; |
| 7. 如果 tg45°=m,那么ctg54°=________,ctg36°=________,tg36°=________。 |
| 8. 在△ABC中,∠C=90° , b=4,c=5,那么a= ,cosA·ctgB= . |
| 9. 如果 tgα·tgα23°=1 ,那么锐角 α=________。 |
| 10. 在△ABC中, AB=AC, AD⊥BC 于点D, 若 AD:BC=√3:2 ,则tgB= ,cosC= . |
| 11. 在△ABC中,∠C=90° , ∠B=30° , S△ABC=4√3 ,那么a= ,b= ,c= . |
| 12. 若锐角x满足 √2sinx=1 ,则锐角x= . |
| 13. 化简 |
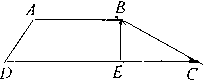
| 14. 如图,水库大坝横断面为梯形ABCD, BE⊥DC ,BE=4,斜坡BC的坡度i=1:√3 ,AB=10,AD=5,则∠BCD ,DC= ,斜坡AD的坡度= .
|
| 15. 已知sinα= |
| 16. 在△ABC中,∠C=90° , c=8, a:b=1: √3 则 ∠A ,a= ,b= , S△ABC . |
| 17. 等腰三角形腰长与底边长度之比为 1:√2 ,则顶角= ,底角= 。 |
| 18. 用符号">""="或"<"表示下列各式子之间的关系: cos65º cos89 ; sin65º sin89º; sin65º cos25º; ctg65º stg89º; |
| 19. 斜坡的坡角为α ,若 sinα= |
| 20. 已知 △ABC 中,∠C=90° ,a :b= √3 ,那么sinA=______,cosA=______,tgA=______,ctgA=______。 |
| 三.判断题 (本大题共 8 分) |
| 1. 角30º的正弦值表示为:sin30°=30° ( ) |
| 2. ctg32º=ctg(90º-58º)=tg58º. |
| 3. tg30º= |
| 4. 角 30º的正弦值等于 |
| 四.解答题 (本大题共 28 分) |
| 1. 如图,在△ABC 中,∠A=90° ,AB=AC,D在AC上,且AD:DC=1:2,求 ∠DBC 的四个三角函数值。
|
| 2. 一个直角三角形的锐角的余弦是方程4x2-2(m+1)+m=0的两根,求m的值。 |
| 3. 已知sinα、 cosα是方程 x2+px+q=0的两个根,求证: p2-2p-1=0。 |
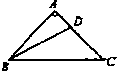
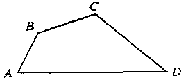
| 4. 如图,四边形ABCD中, ∠ABC=135°, ∠BCD=120°, AB=√6, BC=5-√3, CD=6, 求AD。
|
| 5. (1)tg30+ctg60-tg45+cos90; (2) (3) (4)sina·cos(90º-a)+cosa·sin(90º-a) (a为锐角); (5) |
| 6. 已知如图所示,和岸一侧A处测得对岸一建筑物CB的顶端B的仰角为30º,由A向建筑物走200米到达河边D,测得B点仰角为60º
(1)求河宽DC; (2)求建筑物的高BC。 |
| 7. 如果关于的一元二次方程x2sinα+2x(sinα+2)+sinα+12=0有实数根,试确定锐角α的范围。 |
| 初二几何---解直角三角形 —— 答案 |
|
|
| 一.选择题 (本大题共 24 分) |
| 1. :B |
| 2. :A |
| 3. :D |
| 4. :D |
| 5. :A |
| 6. :D |
| 7. :C |
| 8. :C |
| 9. :B |
| 10. :D |
| 11. :A |
| 12. :C |
| 二.填空题 (本大题共 40 分) |
| 1. :12, 8√3 |
| 2. :3√2 |
| 3. :12,16,20, |
| 4. : |
| 5. :3,30º,60º |
| 6. :1,1,1 |
| 7. : |
| 8. :3, |
| 9. :67° |
| 10. : |
| 11. :2√6, 2√2, 4√2 |
| 12. :45° |
| 13. :1-cosα |
| 14. :30º,13+4√3 ,4:3 |
| 15. : |
| 16. :30°, 4, 4√3, 8√3 |
| 17. :90º,45º |
| 18. :>;<;=;> |
| 19. :5:12 |
| 20. : |
| 三.判断题 (本大题共 8 分) |
| 1. :错 |
| 2. :对 |
| 3. :错 |
| 4. :错 |
| 四.解答题 (本大题共 28 分) |
| 1. :sin∠DBC= |
| 2. :√3 |
| 3. :由题意,有sinα+cosα=-p,sinα·cosα=q,即p=-(sinα+cosα);q=sinα·cosα.则p2-2p-1=[-(sinα+cosα)]2-2(sinα·cosα)-1=0 |
| 4. :AD=2√19提示,作 AE⊥BC 交CB的延长线与点E, DF⊥BC 的延长线与点F,再作 AM⊥DF 与点M,Rt△ABE、Rt△CDF和Rt△AMD 中求解 |
| 5. :(1) |
| 6. :DC=100米,BC=100√3米 |
| 7. :0º<α≤ 30º |
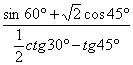 ;
;