初三数学综合试卷

初三数学综合试卷 　　 　　 姓名________　

一填空题:　　　　　　　　　　　　　　　　　　　　　　　　　

1.　　　 －3²的倒数是__________;　x的绝对值等于 ,则x=_______.

2.　　　 12的平方根是_________;　正八边形的每个内角为______.　　　　－2cos45 °_________;

3.　　　 我国现有总人口129533万人,如果以亿为单位,并保留两位小数可以约是________亿人.

4.　　　 －2⁰－（－1）^－1=_________;　分解因式x²-y²+3y-3x=___________________.

5.　　如果x^m=4,xⁿ=8(m,n为自然数),那么x　 =　　　　

6.　　梯形的面积是12cm²,底边上的高线长是4cm,则该梯形的中位线长是　　　　.

7.　　如图,已知D、E分别是△ABC中边AB、BC的中点,

则DE∶AC=　　　　S_△DEB∶S_△ADC=　　　　.

8.　　如图一圆弧形桥拱,拱形的半径为10m,拱的跨

度为16m, 则其拱高等于　　　　

9.　　相交两圆的公共弦长为6,两圆的半径是方程x²-(3　 +5)x+15　 =0 的两根,则两圆的圆心距等于　　　　

10.　　　　 若样本x₁-2,x₂-2,…x_n-2的平均数为10,方差为2,则对于样本x₁+3,x₂+3,…x_n+3的平均数为_____,标准差为________.

11.　 如果函数y=k的图象是双曲线,且在第二,四象限内,那么k的值是　　　　.

12.　 圆锥的底面圆周长是40　 πcm,锥角等于120 °,则它的侧面 开图的面积为　 　　 .

13. 如果两圆的圆心都在x轴上,⊙O的圆心坐标为(7,0),半径为1,⊙O₂的圆心坐标为(x,0),半径为2,当2<x<4时,两圆位置关系是　　　　.

14.　 已知点P (n,2n)是第一象限的点,下面四个命题⑴点P关于y轴对称的点P₁的坐标是(n,-2n)⑵点p到原点O的距离是　 n⑶直线y=-nx+2n不经过第三象限⑷对于函数y=　 ,当x<0时y随x的增大而减小;其中真命题有_________ (填上所有真命题的序号)

15.　　　　 已知⊙O的直径为10 ,弦AB=8cm ,那么AB的弦心距为_______,与AB距离为1cm的平行弦CD的长为__________.

16.　　　　 观察下列规律:1+2+1=2²　 1+2+3+2+1=3² 　 1+2+3+4+3+2+1=16=4² 　 1+2+3+4+5+4+3+2+1=25=5² 计算:1+2+3+…+1999+2000+1999+…+3+2+1=_________________.(用科学记数法表示)

二选择题

1.若k>1,则关于x的方程2x²－(4k+1)x+2k²－1=0的根的情况----------------------------------------------------(　　　 )

(A)有一正根和一负根　　　　(B)有两个正根　　　　(C)有两个负根　　　　　　　  (D)没有实数根

2.下列命题正确的有----------------------------------------------------------------------------------------------------------(　　　　)

⑴既为轴对称图形,又为中心对称图形的四边形为正方形⑵以一条对角线所在直线为对称轴的平行四边形为菱形⑶频数是指一组数据中,落在各个小组内得数据⑷频率分布表中,个小组的频数之和等于样本容量⑸两圆相切,又二条公切线⑹圆周角相等,则所对两弧相等　　　　 (A)2　　　　 (B)3　　　　 (C)4　　　　 (D)5

三计算或解方程

1. －3×　　　　　　　+（）°－（sin30°）　 　 2.　 x²+=12-8x

四　如图,点B、E、F,、C在同一条直线上,AF、DE相交于点O,OE=OF,BE=CF，

∠B=∠C, 求证AB=DC

五. 二次函数y=x²-mx+m-2  (1)试证明此函数图象与x轴有交点(2)当函数图象顶点到x轴距离为时,求函数解析式.

六.　　　　　　　　　 一个批发与零售兼营的商店,凡一次购买铅笔301支(包含301支)可以按批发价付款,购买300支(含300支),只能按零售价付款,现有学生小王来购买铅笔,如果给学校初三年级学生每人买一支,则只能按零售价付款,需用(m²-1)元(m为正整数且m²-1>100),如果多买60支,则可以按批发价付款,同样需用(m²-1)元(1)设这个学校初三年级共有x名学生,则x的取值范围____________;铅笔零售价应为________________批发价每支应为_________元(用x,m的代数式表示).⑵若按批发价购15支比按零售价每购15支少付款1元,试求这个学校初三年级共有多少名学生,并确定m的值.。

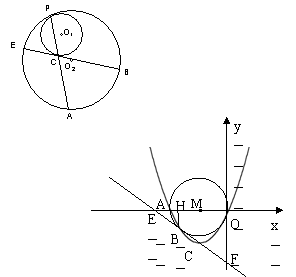
七.如图⊙O₁,⊙O₂内切于点P，⊙O₂的弦BE与⊙O₁相切于点C，PB交⊙O1于D，PC的延长线交⊙O₂于点A，连结AB,CD,PE。⑴求证①∠BPA=∠EPA　　　②　　　　

⑵如图若⊙O₁的切线BE经过⊙O₂的圆心，⊙O₁、⊙O₂半径分别为r、R，其中R≥r，求证PC·AC时定值。

八．如图直角坐标系中，O是坐标原点，A点坐标为（-3,0）,B(m,－)是以OA

为直径的⊙M上一点，且tg∠AOB＝，BH垂直于x轴，垂足为H， ⑴求H点

的坐标　 ⑵求图象经过ABO三点的二次函数解析式　⑶设C点为⑵中二次函数的

图象的顶点，问经过BC两点的直线是否与⊙M相切。说明理由。