初三数学综合练习（四）

初三数学综合练习（四）

姓名　　　　 班级　　　　　 学号

第一部分（100分）

一、填空题（3×16=48分）

1、用代数式表示“数a的3倍与4的差的一半”　　　　　　 。

2、如果a的平方根是±2，那么=　　　　　  。

3、如果一个角的余角等于这个角的补角的3/7，那么这个角=　　　　 度。

4、求值　　　　　 。

5、配上适当的数，使等式　　　　  。

6、如果，那么x=　　　　 。

7、在圆内接四边形ABCD中，∠A∶∠B∶∠C=4∶3∶5，那么∠D=　　　　度。

8、已知菱形的两条对角线长分别是6cm和8cm，那么菱形的周长　　　 cm。

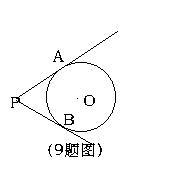
9、如图，PA、PB是⊙O的切线，点A、B是切点，∠APB=78°，点C异于A、B的任意一点，那么∠ACB=　　　　 度。

10、已知0≤x≤3，化简　　　　　 。

11、已知正三角形的边长为a，那么它的内切圆与外接圆组成的圆环面积S=　　　　 。

12、已知扇形的圆心角为150°，弧长为20πcm，那么这个扇形的半径为　　　　  cm。

13、一个反比例函数在第二象限的图象如图所示，点A是图象上任意一点，AM⊥x轴，垂足是M，O是原点，如果△AOM的面积为3，那么这个反比例函数的解析式是y=　　　　。

14、幼儿圆有玩具若干件，分给小朋友，如果每人分3件，那么还余79件，如果每人分5件，那么最后一人还少几件，该幼儿园的小朋友至少有　　　人，玩具至少有　　　件。

　　　　　　　　　　　　　　　　　　　　　　　　　

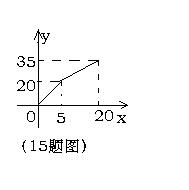
15、有一个附有进、出水管的容器，每单位时间进、出的水量都是一定的，设从某时刻开始5分钟内只进水不出水，在随后的15分钟内既进水又出水，得到时间x（分）与水量y（升）之间的函数关系如图所示，如果20分钟后只放水不进水，那么这时（即x≥20时）y与x之间的函数关系式是　　　　。（要求写出自变量允许值范围）

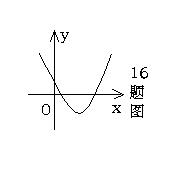
16、已知二次函数的图象大致如图，

那么直线y=bx+c不经过第　　　象限。

二、选择题（3×7=21分）

1、已知实数a、b在数轴上的位置如图　　 a　　　b　　　 所示，那么化简a－b得

A、a－b　　 B、b－a　　C、a+b　　D、－(a+b)

2、用四舍五入法对318.96取近似值，要求保留四个有效数字，那么318.96≈(　　 )

A、318　　  B、318.0　　　 C、319　　　　D、319.0

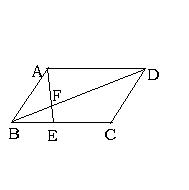
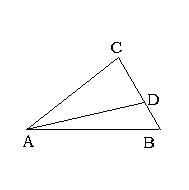
3、如图，平行四边形ABCD中，E是BC上一点，

BE∶EC=2∶3，AE交BD于点F，那么BF∶FD等于（　 ）

A、2∶5　　　B、3∶5　　 C、2∶3　　  D、5∶7

4、二次函数，当x<－2时，y随x的增大而减小；当x>－2时，y随x的增大而增大，那么当x=1时，函数y的值是（　　  ）

A、－7　　　 B、1　　　 C、17　　　 D、25

5、某商品价格为a元，降价10%后又降价10%，销售额猛增，商店决定再提价20%，提价后这种商品价格为（　　　）

A、a元　　B、1.08a元　 C、0.972a元　　D、0.96a元

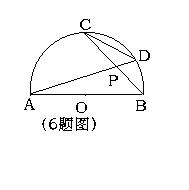
6、如图，AB是半⊙O的直径，弦AD、BC相交于点P，那么CD/AB等于（　　　）

A、sin∠BPD　　 B、cos∠BPD　　  C、tg∠BPD　　　D、ctg∠BPD

7、“一列客车已晚点6分钟，如果将速度每小时加快10千米，那么继续行驶20千米，便可正点运用”，如果设客车原来行驶的速度是x千米/时，那么解决这个问题所列方程是（　　 　）

A、　 　　 B、

C、　　　　D、

三、（8×2=16分）

1、　设a>0，b>0，a≠b；化简：

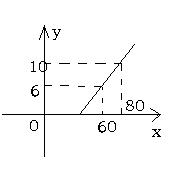2、某地长途汽车客运公司规定旅客可携带一定量的行李，如果超过规定，则需要购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，其图象如图：

求：（1）y与x之间的函数关系式；

（2）旅客最多可免费携带行李的千克数。

四、（7分）

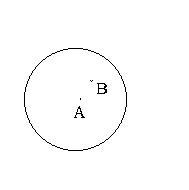如图，某部队在灯塔A的周围进行爆破作业，A的周围3千米内的水域为危险区域，有一渔船误入离A 2千米的B处，为了尽快驶离危险区域，该船应沿哪条射线方向航行？（要求给予证明）

五、（8分）某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每价衬衫每降价1元，商场平均每天可多售出2件。

（1）若商场平均每天盈利1200元，每件衬衫应降价多少元？

（2）每件衬衫降价多少元时，商场平均每天盈利最多？

第二部分（100分）

一、（14分）已知：如图，在△ABC中，∠C=90°，∠BAC=30°，BC=1，D为BC边上一点，tg∠ADC是方程的一个较大的根，求CD的长。（结果取准确值）

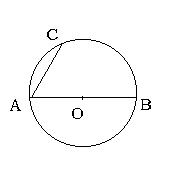二、（14分）已知：如图AB是⊙O的直径，AC是弦，AB=2，AC=，在图中画出弦AD，使AD=1，并求出∠CAD的度数。

三、（14分）2000年全国普通高中和中专（含职高）共招生668万人，而2001年普通高中比上年多招了14.3%，中专（含职高）多招了7.6%，这样高中阶段招生总人数比2000年增加了10.5%，求2000年普通高中和中专（含职高）各招生多少万人（精确到1万人）。

四、（14分）一小船由A港到B港顺流航行需6小时，由B港到A港航行需8小时。一天，小船从早晨6点由A港出发顺流航行到B港时，发现一救生圈在途中掉落在水中，立刻返回，一小时后找到救生圈。总：（1）如果小船按水流速度由A港漂流到B港需要多少小时；（2）救生圈是何时掉入水中的？

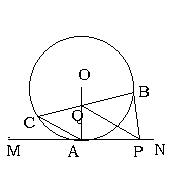五、（14分）已知：直线MN切⊙O于点A，弦BC交半径OA于点Q，BP⊥BC交MN于点P，AC∥PQ，求证：（1）PQ∶2AQ=AO∶AC；（2）

六、（15分）某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A、B两种产品共50件，已知生产一件A种产品需用甲种原料9千克，乙种原料3千克，可获利润700元；生产一件B种产品，需要甲种原料4千克，乙种原料10千克，可获利润1200元。（1）按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来；（2）设生产A、B两种产品获总利润为y（元），其中一种的生产件数为x，试写出y与x之间的函数关系式，并利用函数的性质说明（1）中哪种生产方案获利润最大？最大利润是多少？

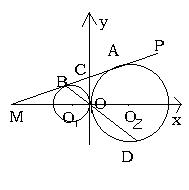七（15分）如图所示，⊙O₁和⊙O₂外切于点O，以直线O₁O₂为x轴，点O为坐标原点建立直角坐标系，直线AB切⊙O₁于点B，切⊙O₂于点A，交y轴于点C（0，2），交x轴于点M，BO的延长线交⊙O₂于点D，且OB∶OD=1∶3。（1）求M、O₂两点的坐标；（2）求直线AB的解析式；（3）求经过M、C、O₂三点的抛物线的解析式；（4）在直线AB上是否存在点P，使△MO₂P与△MOB相似？如果存在，求出点P的坐标；如果不存在，说明理由。