市2003学年第一学期初三期末试卷
数 学 卷
( 2003年12月7日7:40——9:20 )
| 题 次 | 一 | 二 | 三 | 总 分 | ||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||||
| 得 分 | ||||||||||
| 阅卷人 | ||||||||||
一、选择题(本题有12小题,每小题4分,共48分)
1、![]() 的倒数是( )
的倒数是( )
A、
![]() B、
B、
![]() C、
C、
![]() D、
D、
![]()
2、方程x3-4x=0的解是( )
 A、-2,2 B、0,-2 C、0,2 D、0,-2,2
A、-2,2 B、0,-2 C、0,2 D、0,-2,2
3、函数y=―(x―1)2―2的最大值是( )
A ―2 B 2 C ―1 D 1
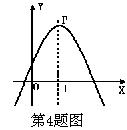
4、如图,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( )
A、x>3 B、x<3 C、x>1 D、x<1
5、下列二次根式中,最简二次根式是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
 6、方程
6、方程![]() 的解的个数是( )
的解的个数是( )
A 4个; B 3个; C 2个; D 1个
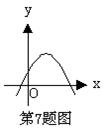
7、二次函数![]() 的图象如图所示,那么下列四个结论:
的图象如图所示,那么下列四个结论:
①![]() <0 ; ②
<0 ; ②![]() >0 ; ③
>0 ; ③![]() >0 ;④
>0 ;④ ![]() <0中,正确的结论有( )
<0中,正确的结论有( )
(A)1个 ( B ) 2个 (C) 3个 (D) 4个
8、已知![]() ,则
,则![]() 的值为(
)
的值为(
)
A ![]() B
B ![]() C
C ![]() D
D ![]()
9、下列二次根式方程中,有实数根的是( )
A ![]() B
B![]()
C ![]() D
D
![]()
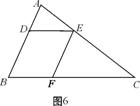
10、如图6,已知DE∥BC,EF∥AB,则下列比例式中,错误的是( )
 (A)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11、把抛物线![]() 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是
的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是![]() ,则有( )
,则有( )
(A)![]()
![]() (B)
(B)![]() ,
,![]()
(C)![]() ,
,![]() (D)
(D)![]() ,
,![]()
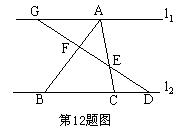 12、如图,直线l1//l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是( )
12、如图,直线l1//l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是( )
A、5:2 B、4:1 C、2:1 D、3:2
二、填空题(本题有6小题,每小题5分,共30分)
13、如果方程![]() 的两根分别为
的两根分别为![]() 和
和![]() ,那么p = ,q = .
,那么p = ,q = .
14、当x =2,y =3时,代数式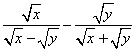 的值为
.
的值为
.
15、CD是Rt△ABC斜边上的高线,AD、BD是方程x2-6x+4=0的两根,则△ABC的面积为 .
16、试写出一个开口方向向上,与X轴有交点,且与y轴的交点坐标为(0,5)的抛物线的解析式 ______________________.
17、已知二次函数![]() 的图象与x轴交于点A、B两点,在x轴上方的抛物线上有一点C,且△ABC的面积等于10,则C点的坐标为_________________.
的图象与x轴交于点A、B两点,在x轴上方的抛物线上有一点C,且△ABC的面积等于10,则C点的坐标为_________________.
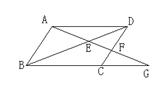 18、如图,平行四边形ABCD中,G为BC延长线上一点,AG与BD交于点E,与DC交于点F,写出图中所有的相似三角形 .
18、如图,平行四边形ABCD中,G为BC延长线上一点,AG与BD交于点E,与DC交于点F,写出图中所有的相似三角形 .
三、解答题(本题有7小题,共72分)下列各小题都必须写出解答过程
19、(本题8分)(1)计算:(—2)0+![]() +
+![]()
(2)在实数范围内分解因式:a2+b2-2ab-3
20、(本题8分)解方程: ![]()
21、(本题10分) 如图,已知△ABC,∠ACB=90º,AC=BC,点E、F在AB上,∠ECF=45º,
如图,已知△ABC,∠ACB=90º,AC=BC,点E、F在AB上,∠ECF=45º,
(1)求证:△ACF∽△BEC
(2)设△ABC的面积为S,求证:AF·BE=2S .
22、(本题10分)已知方程组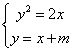 有两个实数解
有两个实数解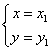 和
和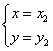 ,且
,且![]() ,求m的值.
,求m的值.
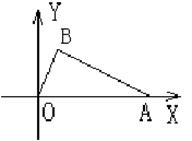 23、(本题10分)如图,已知Rt△OAB的斜边OA在X轴正半轴上,直角顶点B在第一象限,OA=5,OB=
23、(本题10分)如图,已知Rt△OAB的斜边OA在X轴正半轴上,直角顶点B在第一象限,OA=5,OB=![]() .
.
(1)求A、B两点的坐标;
(2)求经过O、A、B三点的抛物线的解析式,并确定抛物线
顶点的坐标.
24.(本题12分)某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:
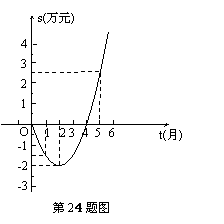 (1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求截止到8月末公司累积利润可达到几万元;
(4)求第8个月公司所获利润是多少万元?
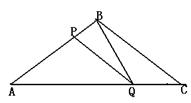 25.(本题12分)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.(1)当x为何值时,PQ∥BC?(2)当
25.(本题12分)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.(1)当x为何值时,PQ∥BC?(2)当![]() ,求
,求![]() 的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由.
的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由.
2003学年第一学期初三教学质量调测数学试卷
参考解答
一、选择题(本题有12小题,每小题4分,共48分)
1、A 2、D 3、A 4、C 5、B 6、B
7、D 8、C 9、C 10、C 11、D 12、C
二、填空题(本题有6小题,每小题5分,共30分)
13、![]() ,1 14、
,1 14、![]() 15、6 16、略 17、(4,5)或(-2,5)
15、6 16、略 17、(4,5)或(-2,5)
18、△AED∽△GEB, △AEB∽△FED, △ABG∽△FCG∽△ADF △ABD∽△CDB
三、解答题(本题有7小题,共72分)
19、(本题8分)
(1)解:原式=1+![]() (3分)=
(3分)=![]() (4分)
(4分)
(2)解:原式=![]() (2分)=
(2分)=![]() (4分)
(4分)
20、(本题8分)
解: 设![]() ,(1分)则原方程变形为: y
,(1分)则原方程变形为: y![]() +2y-8=0. (3分)
+2y-8=0. (3分)
解得y1=-4, y2=2.(4分) ∵![]() 是非负数, ∴ y1=-4 舍去. (5分)
是非负数, ∴ y1=-4 舍去. (5分)
∴![]() =2. 整理, 得 x
=2. 整理, 得 x![]() -3x-4=0. (6分)
解这个方程, 得 x1=
-3x-4=0. (6分)
解这个方程, 得 x1=![]() , x2=4. (7分) 经检验, x1=
, x2=4. (7分) 经检验, x1=![]() , x2=4都是原方程的解. (8分)
, x2=4都是原方程的解. (8分)
21、(本题10分)
(1)证:由已知∠ACB=90º,AC=BC,得∠A=∠B=45º①,(1分)
∠AFC=∠B+∠BCF=45º+∠BCF,(2分)又∠ECF=45º,故∠BCE=∠ECF+∠BCF=45º+∠BCF,(3分)从而∠AFC=∠BCE②,(5分)由①与②证得△ACF∽△BEC (6分)
(2)证:设△ABC的面积为S, S=![]() ,则2S=
,则2S=![]() (7分)
(7分)
由△ACF∽△BEC![]()
![]() (9分)
(9分)![]() AF·BE=AC·BC=2S
(10分)
AF·BE=AC·BC=2S
(10分)
22、(本题10分)
解:将方程![]() 代入
代入![]() 并整理得
并整理得![]() =0,(2分)由
=0,(2分)由![]() ,
,![]() ,(3分)代入已知式得
,(3分)代入已知式得![]() ,(5分)解此方程得
,(5分)解此方程得![]() 或
或![]() ,(7分)而方程组有两个实数解知Δ=
,(7分)而方程组有两个实数解知Δ=![]() =
=![]() ≥0,得
≥0,得![]() ≤
≤![]() ,(9分)因此
,(9分)因此![]() 应舍去,所以m的值为
应舍去,所以m的值为![]() (10分)
(10分)
23、(本题10分)
(1)过B作BD⊥X轴,垂足为D,(1分)由勾股定理得AB=![]() ,(2分)
,(2分)
易证△OAB∽△OBD,得出![]() (3分)∴OD=1,BD=2,(4分)
(3分)∴OD=1,BD=2,(4分)
∴A、B两点的坐标为A(5,0),B(1,2)。(5分)
(2)设所求的解析式为y=a(x-0)(x-5),( 6分)由抛物线过B(1,2)得2=-4a,(7分)
∴a=![]() ,(8分)∴所求的经过O、A、B三点的抛物线的解析式为y=
,(8分)∴所求的经过O、A、B三点的抛物线的解析式为y=![]() ,(9分)且抛物线顶点的坐标是
,(9分)且抛物线顶点的坐标是![]() .(10分)
.(10分)
24、(本题12分,每小题答对给3分)
解:(1)累积利润s(万元)与时间t(月)之间的函数关系式为![]() (
(![]() ≥0);
≥0);
(2)截止到10月末公司累积利润可达到30万元;
(3)截止到8月末公司累积利润可达到16万元;
(4)第8个月公司所获利润是5.5万元.
25、(本题14分)
解:由已知可得AP=![]() cm,BP=(20
cm,BP=(20![]() )cm,CQ=
)cm,CQ=![]() cm,AQ=(30
cm,AQ=(30![]() )cm,(1分)
)cm,(1分)
(1)只要![]() 成立,即
成立,即![]() ,(3分)解之得
,(3分)解之得![]() 时PQ∥BC;(5分)
时PQ∥BC;(5分)
(2)当![]() 即
即![]() 时,由
时,由![]() 得
得![]() ,此时PQ∥BC,从而
,此时PQ∥BC,从而![]() (6分)
(6分)![]()
![]() ,(7分)但
,(7分)但![]() (8分)
(8分)![]()
![]() 的值为
的值为![]() ;(10分)
;(10分)
(注:本小题也可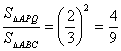
![]()
![]() =
=![]() -
-![]()
![]()
![]() 得到)
得到)
(3)ΔAPQ与ΔCQB能相似(11分).AP的长为![]() cm(13分)和20cm(14分).
cm(13分)和20cm(14分).