海安县2006年初三年级调查考试
数学试卷
本试卷分第Ⅰ卷和第Ⅱ卷两部分，全卷分值130分，答题时间120分钟。
第Ⅰ卷（选择题共28分）
一、选择题（本题共12题，第1－8题每小题2分，第9－12题每小题3分，共28分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
注意事项：下列各题都有A、B、C、D四个结论供选择，其中只有一个正确选项，请把正确选项的代号填入上表题号下的对应位置处。
1、已知
＝2，则下列四个式子中一定正确的是（ ）
A、x=2 B、 x=－2 C、 x2=4 D、x3=8
2、函数y=
中，自变量x的取值范围是（ ）
A、x＞3 B、x≥3 C、x＞－3 D、x≥－3
3、点P（1，－3）关于x轴对称的点坐标是（）
A、（－1，－3） B、（3，－1） C、（1， 3） D、（－3，1）
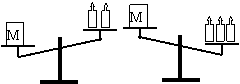4、如图1，天平右盘中的砝码的质量为10g,则物体的质量m(g)的取值范围，在数轴上可表示为（ ）
5、下列二次根式中，属于最简二次根式的（ ）
A、
B、
C、 
D、
6、下列图形中是轴对称图形，而不是中心对称图形的 是（ ）
A、等腰梯形 B、矩形 C、平行四边形 D、菱形
7、一副三角板，如图所示叠放在一起，则图中∠
的度数是（ ）
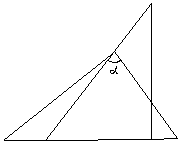
A、 75° B、60° C、 65° D、55°
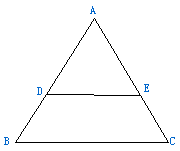
8、如图，DE是△ABC的中位线，则△ADE与四边形DBCE的面积之比是（ ）
A、1：1 B、 1：2 C、1：3 D、1：4
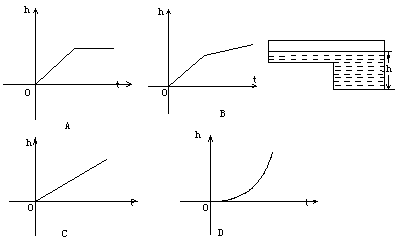9、某蓄水池的横断面的示意图如图，分深水区和浅水区，如果这个蓄水池以固定的流量注水，下面的图象能大致表示水的最大深度h和时间t的关系的是（ ）
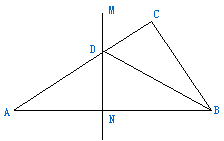
10、如图，在△ABC中，∠C＝90°，AC＝8cm,AB的垂直平分线MN交AC于D，连结BD，若cos∠BDC=
,则BC的长是（ ）
A、4cm B、6cm C、8cm D、10cm
11、已知等腰三角形的腰长为13cm，底边长为10cm,那么它的外接圆的半径为（ ）
A、5 B、
C、
D、12
12、给出下列四个命题：
①如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形；
②若点A在直线y=2x－3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限；
③半径为5的圆中，弦AB＝8，则圆周上到直线AB的距离为2的点共有四个；
④若A（a,m）、B（a－1,n）(a＞0)在反比例函数y=
的图象上，则m＜n.
其中，正确的命题个数是（ ）
A、1个 B、2个 C、 3个 D、4个
第二部分（非选择题，共102分）
二、填空题（本题共6小题，每小题3分，共18分）
13、如图，在△ABC中，BC＝5cm,BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是____________cm。
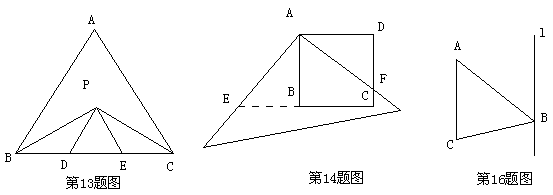
14、如图，有一块边长为3的正方形塑料模板ABCD，将一块足够大的直角三角板的直角顶点落在A点，两条直角分别与CD交于点F，与CB延长线交于点E，则四边形AECF的面积是__________________.
15、抛物线y=x2+bx+c与y轴交于点A，与x轴交于B、C两点，且BC＝2，
＝3，则
C＝___________________________.
16、如图，在直角三角形ABC中，∠ABC＝90°，AC＝4，BC＝3，直线
BC，现将△ABC绕着直线
旋转一周，则所得的几何体的表面积为__________________.
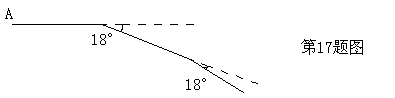
17、如下图，某同学从A点出发前进10米，向右转18°，再前进10米，又向右转18°，这样下去，他第一次回到出发点A时，一共走了______________米。
（第18题图）
18、一质点P从距原点1个单位的A点处向原点方向跳动，第一次跳动到OA的中点A1处，每二次从A1点跳动到OA1 的中点A2处，第三次从A2点跳动到OA2的中点A3处，如此不断跳动下去，则第n次跳动后，该质点到原点O的距离为______________________.
三、解答题（18题8分，19题5分，共13分）
19、（1）cos60°+
-
(2)
÷
20、先化简
÷
，再选择一个你喜欢的x的值代入计算。
四、解答题（每题8分，共48分）
21、张老师在一次“探究性学习”课中，设计了如下数表：
| n | 2 | 3 | 4 | 5 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | … |
| b | 4 | 6 | 8 | 10 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1)请你分别观察a、b、c与n之间的关系，并用含自然数n(n＞1)的代数式表示：
A=________________,b=________________,c=__________________.
(2)猜想：以a、b、c为边的三角形是否为直角三角形？并证明你的猜想。
22、已知关于x的方程kx2-2(k+1)x+k-1＝0有两个不相等的实数根，
（1）求k的取值范围；
（2）是否存在实数k使此方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由。
23、如图，
分别表示一种白炽灯和一种节能灯的费用y（费用＝灯的售价＋电费，单位：元）与照明的时间x(小时)的函数图象，假设两种灯的使用寿命都是2000小时，照明效果一样。（1）根据图象分别求出的函数关系式；
（2）当照明时间为多少小时时，两种灯的费用相等？
（3）小亮房间计划照明2500小时，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法（直接给出答案，不必写出解答过程）。
24、某校初三学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀，下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总分相等，此时有学生建议，可以通过考查数据中的其它信息作为参考，请你回答下列问题：
（1） 计算两班的优秀率。
（2） 分别求出两班的比赛数据的中位数。
（3） 计算两班比赛数据的方差。
（4） 根据以上三条信息，你认为应该把冠军奖状发给哪一个班级？简述理由。
25、如图所示，矩形ABCD中，E为CD的中点，BE⊥AC交AC于点F，过F作FG∥AB，交AE于点G。
（1）求GF：AB的值；（2）求cos∠CAB的值。
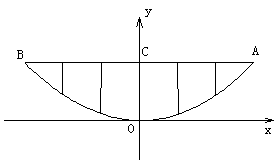
26、某校的围墙上端由一段相同的凹形栅栏组成，如图所示，其拱形图形为抛物线的一部分，栅栏的路径AB间，按相同的间距0.2用5根立柱加固，拱高OC为0.6米。
（1）以O为原点，OC所在的直线为y轴建立平面直角坐标系，请你根据以上的数据，求出抛物线的解析式；
（2）计算这段栅栏所需的立柱的总长度。（精确到0.1米）
五、解答题（27题11分，28题12分，共23分）
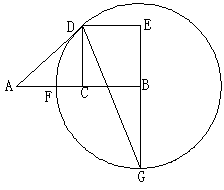
27、设C为线段AB的中点，四边形BCDE是以BC为一边的正方形，以B为圆心，BD长为半径的⊙B与AB相交于F点，延长EB交⊙B于G点，连接DG交于AB于Q点，连接AD。
求证：（1）AD是⊙B的切线；（2）AD＝AQ；（3）BC2＝CF×EG。
28、如图，在平面直角坐标系中，AB、CD都垂直于x轴，垂足分别为B、D且与BC相交于E点，已知：A（－2，－6），C（1，－3）
（1）求证：E点在y轴上；
（2）如果有一抛物线经过A、E、C三点，求此抛物线的解析式；
（3）如果AB位置不变，再将DC水平向右移动k(k＞0)个单位，此时AD与BC相交于E′点，求△AE′C的面积S关于k的函数解析式。
