韦达定理（1） 姓名
1、 说出下列一元二次方程的两实数根的和与两实数根的积；
（1）x2－3x+1=0 x1+x2= ；x1x2= ；（2）3x2－2x－2=0 x1+x2= ；x1x2= ；
（3）2x2－9x+5=0 x1+x2= ；x1x2= ；（4）4x2－7x+1=0 x1+x2= ；x1x2= ；
（5）2x2－4x=0 x1+x2= ；x1x2= ；（6）4x2－5=0 x1+x2= ；x1x2= ；
2、 已知方程5x2+kx－6=0的一个根是2，求另一根及k值。
3、
2+
是方程x2－4x+c=0的一个根，求另一根及c值；
4、 已知方程3x2－19x+m=0的一个根是1，求另一根及m值；
5、 如果－5是方程5x2+bx－10=0的一个根，求另一个根及b值。
6、 利用韦达定理求一元二次方程2x2+3x－1=0的两根的（1）平方和；（2）倒数和
7、
已知x1、x2是方程3x2+px+q=0的两个根，分别根据下列条件求出p、q的值。（1）x1=1，x2=2；（2）x1=3，x2=－6；（3）x1=
，x2=－；（4）x1=－2+，x2=－2－。
8、 设x1、x2是方程2x2+4x－3=0的两个根，求（x1+1）（x2+1）的值。
9、
设x1、x2是方程2x2－6x+3=0的两个根，，利用根与系数的关系，求下列各式的值。（1）x12x2+x1x22；（2）（x1+
）（x2+
）；（3）
；（4）+；（5）
10、
已知方程2x2+ax－2a+1=0的两个实根的平方和为
，求a的值；
11、 设x1、x2是方程x2－2（k-1）x+k2=0的两个实根，且x12+x22=4，求k值。
12、 已知方程x2+（2k+1）x+k2－2=0的两个实根的平方和为等于11，求k的值。
13、
设α、β是方程x2+2x－9=0的两个实数根，求
和α2β+αβ2的值。
14、 已知关于x的方程x2-2(m-2)x+m2=0问：是否存在实数m，使方程的两个实数根的平方和等于56，若存在，求出m的值；若不存在，请说明理由。
韦达定理常用的几个公式：
x12+x22=-（x1+x2）2－2x1x2，（x1－x2）2=（x1+x2）2－4x1x2，
x13+x23=-（x1+x2）3－3x1x2（x1+x2），
，
，
，
，
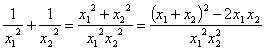（x1+k）（x2+k）=x1x2+（x1+x2）+k2，