数学能力专题训练二（填空题解法）
要点：
填空题有两类：一类是定量的，一类是定性的。填空题大多是定量的，近几年才出现定性型的具有多重选择性的填空题。
填空题缺少选择支的信息，故解答题的求解思路可以原封不动地移植到填空题上。但填空题既不用说明理由，又无须书写过程，因而解选择题的有关策略、方法有时也适合于填空题。
填空题大多能在课本中找到原型和背景，故可以化归为我们熟知的题目或基本题型。填空题不需过程，不设中间分，更易失分，因而在解答过程中应力求准确无误。
解答填空题的常用方法有：
①直接法：直接从题设条件出发，准确计算，讲究技巧，得出结论。
1.在数列{an}中，记Sn=a1+a2+…+an，已知a1=2S2+1，a4=2S3+1,则公比q=__________.
2.点M与点A（4，0）的距离比它与直线x+1=0的距离小1，则点M的轨迹方程是_________.
3. 若正数a、b满足：ab=a+b+3,则ab的取值范围是_______________.
4.
的值是_____________________.
5.函数y=
的值域是___________________.
②特例法：当填空题暗示结论唯一或其值为定值时，可取特例求解。
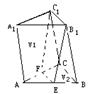
6.如图，三棱柱ABC—A1B1C1中，若E、F分别为AB、AC的中点，平面EB1C1F将三棱柱分成体积为V1、V2的两部分，那么V1：V2=_______________.
7.已知等差数列{an}的公差d≠0,a1、a3、a 9成等比数列，则
的值为_________________________.
8．已知A+B=
，则
的值为____________________.
③数形结合法：借助于图形进行直观分析，并辅之以简单计算得出结论。
9.对任意x(0,1),恒有2x2+(a+1)x-a(a-1)<0成立，则实数a的取值范围是________________.
10．已知a<0，则不等式
的解集为______________.
11.在球面上有四个点P、A、B、C，PA、PB、PC两两互相垂直，且PA=PB=PC=a，那么这个球面的面积是______________________.
请尝试用上述方法求解下列问题：
12．设集合A={x2log2x+log22x≤0},B={x
x-a<4,a∈R,x∈R},如果A
B,则实数a的取值范围是________________.
13．函数f(x)的定义域为R，对于任意的x∈R,恒有f(1-x)+f(1+x)=2,若f(5)=6,则f(-3)=__________________.
14.若函数f(x)=loga(2-ax)在[0,1]上是增函数，则a的取值范围是________________.
15．已知
，则f-1(
)=____________________.
16.不等式
的解集为{xx<1或x>2}，则a=______________.
17．在ΔABC中,a、b、c成等比数列,则cos(A-C)+cos2B+cosB的值为____________.
18.已知复数z=
的模为
,其中a为负实数,则复数z的三角形式为________________.
19.若函数f(x)满足:f(x+1)=f(3-x),且方程f(x+2)=0恰有5个不同的实根,则这些实根之和为____________.
20.虚数z满足z3=8,则z3+z2+2z+2的值为___________________.
21.椭圆的中心在原点，以坐标轴为对称轴，其短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2
，且∠F1BF2=
,则椭圆方程为_________________.
22.在复平面内，复数z满足arg(z-2)=
则
的值为___________.
23.一天中,有政治、语文、数学、英语、物理、体育六节课,体育不在第一节上,数学不在第六节上,这天的课表的不同排法种数为________________.(要求用数字作答)
24.设有编号为1、2、3、4、5的五个球和编号为1、2、3、4、5的五个盒子,现将这五个球投放入这五个盒子内,要求每个盒子放一个球,若恰好有两个球的编号与盒子编号相同,则这样的投放方法总数是________________.(要求用数字作答)
25．（cos2α+sec2α-2）5展开式中，不含α的项是_______________.
26.设{an}为等差数列，Sn为其前n项和，若
则公差d=___________.
27. 数列{an}的前n项和为S= n2+3n+1,则a1+a3+a5+…+a21=__________________.
28.对任意实数α、β的下列命题：
①tgαctgα=1;
②sec(α+β)=
③sinαsinβ=
[cos(α-β)-cos(α+β)]; ④
⑤α、β都在第二象限，且α>β，则cosα<cosβ.
其中不正确的命题序号是__________________.
29.若双曲线的两条渐近线方程为
，它的一个焦点为（0，
），则它的两条准线之间的距离为__________________.
30.已知正方体ABCD—A1B1C1D1，在它们各个侧面的对角线中，与侧棱AA1异面且成45O角的有__________________条.
31．过球的中心的10个平面，其中任三个平面都不交于同一条直线，它们将平面分成m个部分，则m=_______________.
32.对于任意实数x、y,函数f(x)满足f(x+y)=f(x)+2[f(y)]2，且f(1)≠0，则f(2001)=_______________.