初三数学第一学期期末测试
班级_______________学号______________姓名_____________________
一、选择题：（每题2分，共28分）
1、若m>0,n<－2，则（m，n+2）在 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2、下列函数中，正比例函数是 （ ）
A．
B．
C．
D．
3、在Rt△ABC中，∠C=90°，a,b,c分别是∠A、∠B、∠C的对边，下列关系式中，错误的是 （ ）
A．
B．
C． D．
4、若一次函数
图象经过
（ ）
A．第一、二、三象限 B．第一、三、四象限
C．第二、三、四象限 D．第一、二、四象限
5、若函数
的值是1，则
的值是
（ ）
A．1
B．
C．
D．
6、下列方程中有实数根的是 （ ）
A．
B．
C．
D．
7、若方程
的两个实根互为相反数，则
的值是 （ ）
A．0 B．2 C．－2 D．－２或2
8、如果方程
有增根，那么增根是
（ ）
A．2 B．－2 C．－2或2 D．0
9、下列四个函数中,当
>0时,
随的增大而减小的是
( )
A．
B．
． C。
D．
10、下列命题中的假命题是 （ ）
A．半圆所对的弦是直径 B。半圆所对的圆周角是直角
C．不在一直线上的四点确定一个圆 D。圆内接菱形是正方形
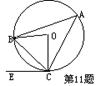
11、如图，△ABC内接于⊙O，EC切⊙O于点C，∠BOC=76°，则∠BCE等于 （ ）
A．14° B．38° C．52° D．76°
12、⊙O的外切等腰梯形ABCD的中位线长等于10，则⊙O的半径长为 （ ）
A．1 B．2 C．3 D．4
13、已知四边形ABCD内接于圆，并且∠A：∠B：∠C=2：3：4，则D的度数是（ ）
A．40° B．60° C．80° D．90°
14、如图，AC、BC分别是半圆O和半圆O′的直径，半圆O的弦PC交半圆O′于Q，PQ=1，设∠PCA=α，则AB等于
（ ）
A．
B．
C．
D．
二、填空题（每空2分，共26分）
15、抛物线
的顶点坐标是_________________.
16、PA、PB分别切⊙O于A、B，∠APB=80°，点C是⊙O上异于A、B任一点，则∠ACB=_______.
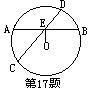
17、已知：如图⊙O的弦AB、CD相交于点E，OE⊥AB，CE=8，DE=5，则AE=________;若OE=3,则⊙O的半径=____________.
18、函数
中自变量的取值范围是____________________.
19、若点A
与B
关于x轴对称,则=_______________.
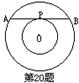
20、如图,在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，设AB=12，则两圆构成的圆环面积为___________________.
21、⊙O的半径为5cm，弦长为6cm的中点的轨迹是______________________________.
22、已知为θ锐角,且
,那么
=_____________
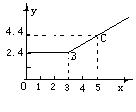
23、图中的折线ABC为甲地向乙地打长途电话所需付的电话费y（元）与通话时间t（分钟）之间的函数关系的图象，当
3时，该图象的解析式为__________________;从图象中可知,通话2分钟需付电话费_________元;通话7分钟需付电话费________元.
25、某工厂把500万资金投入新产品开发，一年后获得了一定的利润，在不抽资金和利润的前提下，第二年的利润比第一年的利润率增加8%，这样第二年净利润为105万元，为求第一年的利润率，可设它为x，则所列方程为________________________.
三、解答题
26、（本题8分）解方程（组）
（1）
（2）
27、（本题6分）已知二次函数
的图象与轴有两个交点,
(1)求的取值范围;(2)当这两个交点的横坐标的平方和等于7时,求的值.
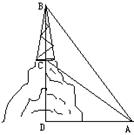28、（本题5分）由地面上A点测得山顶电视塔顶点B和电视塔基地C点的仰角为60°和30°,已知山顶C到地平面的垂直高度为40米.求电视塔高BC.
29、（本题6分）某市调查家庭生活费用情况，发现每月的生活费用y（元）的一部分与家庭人数x(人)成正比，比例系数为k,而另一部分与家庭人数无关，是一笔固定支出b元。已知3人家庭各4人家庭的生活费用如下表，请根据平均月生活费用情况推算出5人家庭一年的生活费用是多少？
| 家庭人数 | 月数 | 生活费用（元） |
| 3 | 5 | 7000 |
| 4 | 6 | 10800 |
30、（本题6分）在△ABC中，∠C=90°，斜边AB=10，直角边AC、BC的长是关于x的方程
的两实数根。
（1）求
的值；（2）计算sinA+sinB+sinA·sinB
31、（本题7分）(本题7分)如图，在△ABC中，∠C=90°，BE是角平分线，DE⊥BE交AB于D，⊙O是△BDE的外接圆，
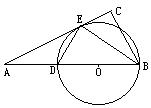（1）求证：AC是⊙O的切线。（2）若AD=6，AE=
，求DE的长。
32、(本题8分)已知抛物线
的对称轴为
顶点在上,A、B为抛物线与的轴的两个交点，，点A在点B的左边，点P为抛物线与轴的交点。
（1）求抛物线的解析式；（2）求△PAB的面积；
（3）当点P在轴上方的抛物线上移动，问移到什么位置上，△PAB面积最大，并求出△PAB的最大面积。