2005—2006学年度第一学期期末考试
九年级数学(华师版)试题
本试卷分第一卷(选择题)和第二卷(非选择题)两部分.满分150分.考试时间120分钟.
第一卷(选择题,共48分)
一、选择题(下列各小题的四个选项中,只有一个符合题意,每小题4分,共48分)
1.0.000045用科学记数法可表示为 ( )
A、4.5×10-4 B、4.5×10-5 C、45×10-4 D、45×10-5
2.已知点A的坐标为(-3,4),⊙A经过原点,则⊙A与x轴的另一个交点的坐标为 ( )
A、(-4,0) B、(-5,0) C、 (-8,0) D、(-6,0)
3.若一元二次方程2x2+k=0有实数根,则k的取值范围是 ( )
A、 k>0 B、 k≥0 C、 k<0 D、 k≤0
4.若一元二次方程x2-2x-3=0的两根为x1和x2,则x1+x2的值为( )
A、-2 B、-3 C、2 D、3
5.下列计算结果正确的是 ( )
A、 m6÷m2=m3 B、 (ab)6÷(ab)2=a4b4
C、 2x2·3x3=6x6 D、 ()3=
6.小明用一个圆心角为120°,半径为9厘米的扇形做一个圆锥的侧面(接缝忽略不计),那么,做成的圆锥底面半径为 ( )
A、4厘米 B、3厘米 C、2厘米 D、1厘米
7.两个三角形具备下列条件但不一定全等的是 ( )
A、两边及一边的对角对应相等 B、两角及夹边对应相等
C、两边及夹角对应相等 D、三边对应相等
8.若ab≠O,则分式的取值不可能是 ( )
A、0 B、1 C、2 D、-2
9.用配方法解方程x2-4x-1=0,下列变形正确的是 ( )
A、(x-2)2=5 B、(x-4)2=1 C、(x-2)2=1 D、(x-4)2=5
10.我们经常玩一种叫“锤子、剪子、布”的游戏,当你出“剪子”时,对手赢你的概率是 ( )
A、 B、 C、 D、
11.随着科学技术不断发展,我国列车行驶的速度越来越快,2004年4月18日,全国铁路进行了第五次大提速,提速后,1000千米的路程省时5.6小时,若提速前列车行驶的速度为x千米/小时,提速后列车行驶的速度为y千米/小时,则x,y应满足的关系式为 ( )
A、x-y= B、y-x= C、=5.6 D、=5.6
12.为了方便简捷地了解总体的状况,我们常会从总体中抽取样本,然后用样本特征去估计总体特征。但是样本抽取要合理,那么,你认为下列抽取样本合理的是 ( )
A、为了了解全市初三学生中考成绩,从全市4万名考生中随机抽取6名考生数学成绩
B、市文化局为了了解该市市民家庭藏书量,到一所重点中学调查了20名教师的家庭藏书量
C、为了了解某市的卫生状况,检查组检查了该市3所最大的商场的卫生情况
D、为了了解全校学生对学校一项新规定的意见,校长室从各班抽取了学号末位是5的同学调查了解
第二卷(非选择题,共102分)
二、填空题(本题共6小题,每小题4分,共24分)
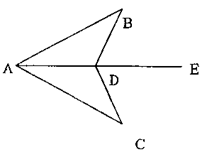
13.如图,点D在射线AE上,∠BDE=∠CDE,若只允许添加一个条件,并使得△ADB≌△ADC,那么你所添加的条件是________。
14.将命题“平行四边形对角线相等”改写成“如果……,那么……”的形式为________。
15.在数学老师的成绩记录单上,初三(8)班小明的平时成绩为85分,期中成绩为70分,期末成绩为90分.若该校规定:学期成绩按平时成绩占30%,期中成绩占30%,期末成绩占40%计算,那么小明的学期成绩为________分。
16.对于一元二次方程ax2+bx+c=0(a≠0)的系数a,b,c若有a+b+c=0和a-b+c=0成立,则方程的两个根为________。
17.一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为________cm2。
18.同时投掷两枚普通的正六面体骰子,点数的和为6的概率是________。
三、解答题(共78分,解答应写出必要的计算过程、推演步骤或文字说明)
19.计算(10分,每题5分)(1)化简:-x+1)
(2)、(a2b)2·(-)3÷(-)4 , 其中a=()0,b=(-)-2。
20.(本题满分7分)
解分式方程:
21.(本题满分7分)
已知:线段a、直线l及l上的一点A,
求作: ⊙O,使⊙O与直线l相切于点A,且半径等于a。
(不写作法,但保留作图痕迹)
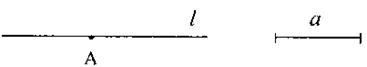
22.(本题满分8分)
一只袋子里装了1只红球和2只黑球,甲、乙两同学玩摸球游戏,游戏规则是:甲每次从袋中拿两遍球(每遍只能取一个,取后放回),只要有一遍是红球,甲就得1分(若两遍都是红球,也只得1分);乙每次从袋中拿一个球,若是黑球,乙就得1分.每人进行10次,谁得分高谁赢.那么你认为谁赢的可能性大?为什么?
23.(本题满分8分)
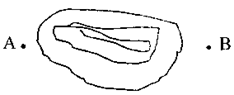
如图,一池塘东西两旁有A、B两棵古树,现想测量出这两棵古树间的距离,请你根据所说过的全等三角形知识设计出测量方案,并叙述你所设计的理由.
24.(本题满分8分)
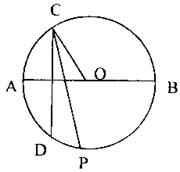
已知AB为⊙O的一条定直径,它把⊙O分成上下两个半圆,点C在上半圆,弦CD⊥AB,∠OCD的平分线交OO于点P。试说明:不论点C在上半圆上如何移动(不与A、B重合,且CD不经过点O),点P的位置都不变.
25.(本题满分9分)
某县平原绿化的迅速发展带到了林业产业的迅速发展。该县某胶合板厂2002年的全年利税是40万元,2004年的全年利税是100.8万元,如果2004年利税增长率是2003年利税增长率的2倍,求该厂2003年的全年利税。
26.(本题满分9分)
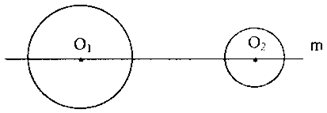
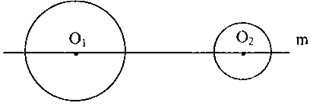
如图,己知⊙O1和⊙O2的半径分别为4厘米和2厘米,圆心O1、O2都在直线m上,且O1O2=22厘米,若⊙O1和⊙O2分别以3厘米/秒和1厘米/秒的速度同时向对方运动,设运动的时间为t
(Ⅰ)当t为何值时,两圆外切;
(Ⅱ)设两圆相交时其中一个交点为A,当t为何值时,△AO1O2是以点A为直角顶点的直角三角形.
27.(本题满分12分)
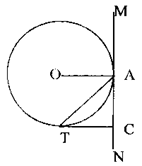
小明在⊙O上取一点A,过A点作⊙O的切线MN,然后作∠OAN的平分线交⊙O于点T,过点T作TC⊥MN于点C(如上图).
(Ⅰ)试说明TC是⊙O的切线;
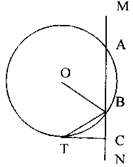
(Ⅱ)若小明将直线MN向圆心O处移动,使之成为⊙O的割线(如下图),交点为A、B,这时小明又什∠OBN的平分线交⊙O于点T(BT与⊙O有交点)过点T作TC⊥MN于点C.这时TC还是⊙O的切线吗?为什么?
(Ⅲ)在(Ⅱ)中,若过点B的直径与TC的延长线交于点D,且AB=4,BD=3,试求线段BT的长。