2005—2006学年度初三(实验班)第四次月考测试试卷
姓名 学号 成绩
一.选择题(每题4分,共40分,把正确的答案填在下面的答题表内,否则不给分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1.![]() 的值是
的值是
(A) ![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D) ![]()
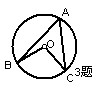 2.不解方程,判别方程
2.不解方程,判别方程![]() 的根的情况是
的根的情况是
(A) 有两个相等的实数根 (B) 有两个不相等的实数根
(C) 只有一个实数根 (D) 没有实数根
3.如图,已知圆心角∠BOC =![]() ,则圆周角∠BAC的度数是
,则圆周角∠BAC的度数是
 (A)
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
4.如图,两条宽为![]() 的纸条交叉重叠在一起,且它们的交角为
的纸条交叉重叠在一起,且它们的交角为![]() ,则
,则
它们重叠部分面积(图中的阴影部分面积)为
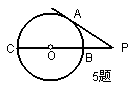 (A)
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
5.如图,BC是⊙O的直径,P是CB延长线上一点,PA切⊙O于A,
如果PA =![]() ,PB =
,PB =![]() ,则∠APC的度数是
,则∠APC的度数是
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
 6.如图,直线AB切⊙O于A,割线BDC交⊙O于D、C,若∠C =
6.如图,直线AB切⊙O于A,割线BDC交⊙O于D、C,若∠C =![]() ,
,
∠B =![]() ,则∠ADC的度数是
,则∠ADC的度数是
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
7.某大坝的横断面是等腰梯形,坡角为![]() ,则坡度为
,则坡度为
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
8.圆内接四边形ABCD的四个内角:∠A、∠B、∠C、∠D的度数可比为:
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
9.若![]() 、
、![]() 是方程
是方程![]() 的两个实数根,则
的两个实数根,则![]()
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D) ![]()
10.如果一定值电阻R两端增加电压![]() 时,通过它的电流为
时,通过它的电流为![]() ,那么通过这一电阻的电流
,那么通过这一电阻的电流![]() 随它的两端电压
随它的两端电压![]() 变化的图象是
变化的图象是

(A) (B) (C) (D)
二.填空题:(每题4分,共24分)
11.关于![]() 的方程
的方程![]() 是一元二次方程,则
是一元二次方程,则![]() 满足的条件是
;
满足的条件是
;
12.已知![]() 是方程
是方程![]() 的一个根,那么代数式
的一个根,那么代数式![]() ;
;
13.在Rt⊿ABC中,若AC =![]() ,BC =
,BC =![]() ,AB =
,AB =![]() ,则
,则![]() ;
;
 14.半径为
14.半径为![]() 的⊙O中两条平行弦AB、CD分别长为
的⊙O中两条平行弦AB、CD分别长为![]() 、
、![]() ,则AB、CD之间的距离为
;
,则AB、CD之间的距离为
;
15.如图:反比例函数![]() 的图象上有一点P,PA⊥
的图象上有一点P,PA⊥![]() 轴于A,
轴于A,
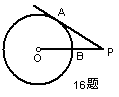 PB⊥
PB⊥![]() 轴于B,矩形ONPA的面积为
轴于B,矩形ONPA的面积为![]() ,则反比例函数的解析式为
;
,则反比例函数的解析式为
;
16.如图,PA切⊙O于A,PO交⊙O于B,若PA =![]() ,PB =
,PB =![]() ,
,
那么⊙O的半径为 ;
三.解答题:
17.解方程:(每小题6分,共12分)
(1)![]() (2)
(2)![]()
18.解方程组:(8分)![]()
19.(10分)计算:![]()
20.(10分)已知,如图,AD是⊿ABC的外角∠EAC的平分线,AD与三角形ABC的外接圆相交于点D,求证:DB = DC;

21.(12分)如图:何新家居住的甲楼AB面向正北,现计划在他家居住的楼前修一座乙楼CD,楼高约为![]() ,两楼之间的距离为
,两楼之间的距离为![]() ,已知冬天的太阳最低时,光线与水平线的夹角为
,已知冬天的太阳最低时,光线与水平线的夹角为![]() ;
;
(1)试求乙楼CD的影子落在甲楼AB上高BE的长;
(2)若让乙楼的影子刚好不影响甲楼,则两楼之间的距离至少应是多少?(精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)

22.(10分)阅读下列解题过程:
题目:已知方程![]() 的两个根为
的两个根为![]() 、
、![]() ,求
,求![]() 的值;
的值;
解:∵![]()
∴![]() ①
①
由一元二次方程根与系数的关系得:![]() ,
,![]() ②
②
∴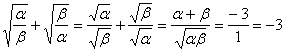 ③
③
阅读后回答问题:
上面解题过程是否正确?若不正确,指出错在哪里?并写出正确的解题过程。
23.(12分)已知一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象在第一象限内的交点是
的图象在第一象限内的交点是
P![]() ,
,![]() ,(1)求
,(1)求![]() 的值;(2)求一次函数和反比例函数的解析式;
的值;(2)求一次函数和反比例函数的解析式;
24.(12分)如图,∠B =![]() ,O是AB上一点,以O为圆心OB为半径的圆与AB交于点E,与AC切于点D,若AD =
,O是AB上一点,以O为圆心OB为半径的圆与AB交于点E,与AC切于点D,若AD =![]() ,且AE、AB的长是关于
,且AE、AB的长是关于![]() 的方程
的方程![]() 的两个实根;
的两个实根;
(1)求⊙O的半径;
(2)求CD的长;

参考答案
一.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | A | A | B | B | D | A | A | D |
二.
11.![]() ;
;
12.![]() ;
;
13.![]() ;
;
14.![]() 或
或![]() ;
;
15.![]() ;
;
16.![]() ;
;
三.
17.(1)![]() ,
,![]() ; (2)
; (2)![]() ,
,![]() ,
,![]() ,
,![]() ;
;
18.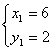 ,
, ;
;
19.原式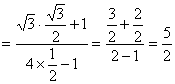 ;
;
20.证明: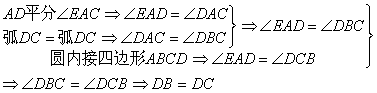
21.(1)过点E作EG∥FD交CD于点G,则有:
在Rt⊿CGE中
∵∠CEG =![]()
∴CG =![]()
∴![]()
答:乙楼CD的影子落在甲楼AB上高BE的长是![]() 。(不答扣1分)
。(不答扣1分)
(2)在Rt⊿CFD中
![]()
答:两楼之间的距离至少应是![]() 。(不答扣1分)
。(不答扣1分)
22.不正确。第③步出错。
应为:
解:∵![]()
∴![]()
由一元二次方程根与系数的关系得:![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
23.(1)∵P![]() ,
,![]() 在一次函数
在一次函数![]() 上,
上,
∴![]() ,即
,即![]()
又∵P![]() ,
,![]() 在反比例函数
在反比例函数![]()
![]() 上,
上,
∴![]() ,即
,即![]()
∴![]()
∴![]()
(2)∵![]()
∴所求一次函数的解析式为:![]() ,反比例函数的解析式为:
,反比例函数的解析式为:![]() ;
;
24.(1)连结DE、BD,
∵AD是⊙O的切线,∴∠ADE =∠ABD,∠A =∠A,
∴⊿ADE∽⊿ABD,∴![]()
又∵AD =![]() ,∴
,∴![]()
又∵AE、AB的长是关于![]() 的方程
的方程![]() 的两个实根
的两个实根
∴![]() ,
,
∴![]()
∴原方程为![]() 的两根为:
的两根为:![]() ,
,![]() ;
;
 ∴
∴![]() ,
,![]()
∴⊙O的半径为![]() ,
,
(2)∵CB⊥AB,AB经过圆心O,
∴CB切⊙O于点B,
∴CD = CB
在Rt⊿ABC中,
设CD =![]() ,则
,则![]()
∴![]()
∴![]()
解得:![]()
∴![]()