初三数学总复习测试十四模拟试卷一
班级 姓名 学号 得分
卷 一
一、选择题（本题共有12个小题，每小题都有A、B、C、D四个选项，请你把你认为适当的选项前的代号填入下面表格的相应位置中，每小题有且只有一个答案正确，多选、不选、错选均不给分，每小题4分，共48分）
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答 案 | ||||||
| 题 号 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 |
1、―3的倒数是（ ）（2001湖州）
A 3 B 
C ―3 D ―
2、若x>1，则化简
的结果是（
）（2001广西）
A 1―2 B x―1 C 1+x D ―(1+x)
3、若x1，x2是方程3x2+x―1=0的两个根，则
的值是（ ）（2001河北）
A ―1 B 0 C 1 D 2
4、函数y=
中，自变量x的取值范围是（
）（2001北京朝阳）
A x≥2 B x>―2且x≠―1 C x≠―1 D x≥―2且x≠―1
5、用配方法将函数y=
x2―2x+1写成y=a(x+m)2+k的形式是（
）（2001陕西）
A y= (x―1)2―3 B y= (x―1)2―1 C
y= (x―2)2―3 D y= (x―2)2―1
6、一木工师傅现有两根木条，木条的长分别是40cm和50cm，他要选择第三根木条，将它们钉成一个三角形木架，设第三根木条的长为xcm，则x的取值范围是（ ）（2001乌鲁木齐）
A 10cm<x<90cm B 20cm<x<100cm C 40cm<x<50cm D 90cm<x<200cm
7、下面给出的条件中，能判定四边形ABCD为平行四边形的是（ ）
A AB∥CD，AD=BC B AB=AD，CB=CD
C AB=CD，AD=BC D ∠B=∠C，∠A=∠D
8、如果α是锐角，且cosα=
，那么sinα的值是（
）（2001广州）
A 
B C 
D 
9、已知两圆的半径分别为3和7，圆心距为5，则这两圆的公切线最多有（ ）（2001北京东城）
A 1条 B 2条 C 3条 D 4条
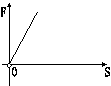
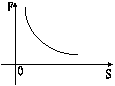
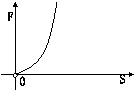
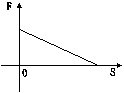10、已知力F所作的功是15焦，则力F与物体在力的方向上通过的距离S的图像大致是（ ）（2001安徽）
A B C D
11、已知：如图，△ABC中，AD⊥BC于D，下列条件：（1）∠B+∠DAC=90°；
（2）∠B=∠DAC；(3)
；(4)AB2=BD·BC。其中一定能够判定△ABC
是直角三角形的共有（ ）（2001山西）
A 3个 B 2个 C 1个 D 0个
12、如图，施工工地的水平地面上，有三根外径都是1米的水泥管
两两相切摞在一起，则其最高点到地面的距离是（ ）
（2001山东临沂）
A 2 B 1+
C 
D 1+
卷 二
二、填空题（本题共有6个小题，每小题5分，共30分）
13、化简ab―2ab= （2001江西）
14、不等式3(x+1)≥5x―3的正整数解是 。（2001吉林）
15、如果圆柱的母线长为3cm，底面半径为2cm，那么这个圆柱的侧面积是 cm2（2001北京海淀）
16、如果梯形的两底之比为2∶5，中位线长14厘米，那么较大的底的长为
厘米。（2001上海）
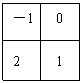
17、如图，沿正方形对角线对折，互相重合的两个小正方形内的数字
的积等于 。（2001吉林）
18、如果等腰三角形 ，那么这两个等腰三角形全等
（只填一种能使结论成立的条件即可）（2001山西）
三、解答题(本题共有7个小题，其中19、20、21小题每题8分，22小题10分，23、24小题每题12分，25小题14分，共72分)
19、计算：∣1―
∣+5×()―1+(―2001)0―
（2001青海）
20、如图，△ABC中，AB=AC，外角∠CAD=100°，求∠B的度数
21、已知：关于x的方程x2+kx―1=0
（1）求证：方程一定有两个不相等的实数根
（2）若方程的两根分别为x1，x2，且
=2―
，求k的值
22、实际中存在着大量的如下关系：路程=速度×时间；工作量=工作效率×工作时间；溶质=溶液×质量分数；……，即三个量a、b、c之间存在数量关系a=bc。现在请编一道含有这种关系的应用题，要求：
（1）用“行程问题”、“工程问题”、“化学浓度问题”以外的其他贴近实际的素材编制
（2）仅编“已知两个量求第三个量”的实际问题，并正确解答的最多得8分
（3）编题或解答中有创新的另加2分。（2001福建三明）
23、如图，△ABC中，AB=AC=5，BC=6，P为AC上的一点（点P与点C重合），点P到点C距离为x，△BPC的面积为y，求y与x的函数关系式，并写出x的取值范围
24、台风是一种自然灾害，它以台风中心为圆心在周围数十千米内形成气旋风暴，有极强的破坏力。据气象观测，距沿海某城市A的正南方向220千米B处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级。该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动，且台风中心风力不变。若城市所受风力达到或超过四级，则称为受台风影响。
（1）该城市是否受到这次台风的影响？请说明理由。
（2）若会受到台风影响，那么台风影响该城市的持续时间有多长？
（3）该城市受到台风影响的最大风力为几级？（2001重庆）
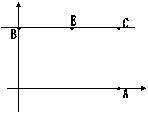
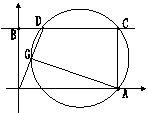
25、如图，在平面直角坐标系内，A、B、C三点的坐标分别是A(5，0)，B(0，3)，C(5，3)，O为坐标原点，
（1）点E在直线BC上，若△AEO为等腰三角形，求E点的坐标。（不必写出计算过程）
（2）过A、C两点的⊙O1交线段BC于另外一点D，且⊙O1与y轴没有公共点，OD交⊙O1于点G，设D点的横坐标为t，△OGA的面积为S，试用含t的代数式表示S，并求t的取值范围
 |