九年级（上）第一次数学月考试题

九年级（上）第一次数学月考试题（满分150分）

一、选择题（每题4分，共48分）

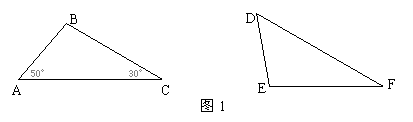
1．如图1，若△ABC≌△DEF，则∠E等于

A．30°　　　　  B． 50°　　　　C．60°　　　　　 D．100°

2． 下列方程中，是一元二次方程的是

A 　　　　　　　　　B  

C 　　　　　　　D

3．如图2，一棵大树在一次强台风中于离地面5米处折断倒下，倒下部分与地面

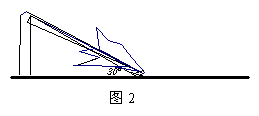成30°夹角，这棵大树在折断前的高度为

A．10米　　　  B．15米　　　　

C．25米　　　　D。20米

4．到△ABC的三个顶点距离相等的点

是△ABC的

A.三边中线的交点　 B.三条角平分线的交点　 C.三边上高的交点　 D.三边中垂线的交点

5．角平分线的尺规作图，其根据是构造两个全等三角形，由作图可知：判断所构造的两个三角形全等的依据是

A.SSS　　 B.ASA　　 C.SAS　　 D.AAS

6． 把方程化成一般式，则、、的值分别是

A .　　 B.　　 C .　　 D .

7．△ABC中，∠A∶∠B∶∠C=1∶2∶3，CD⊥AB于点D若BC=a，则AD等于

A.a　　 B.a　　 C.a　　 D.a

8．如图，等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是

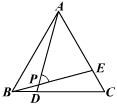A.45°　　 B.55°　　 C.60°　　 D.75°

9．从正方形的铁皮上，截去2cm宽的一条长方形，

余下的面积是48cm²，则原来的正方形铁皮的面积是

A.9cm²　　 B.68cm²　　 C.8cm²　　 D.64cm²

10．一架长2.5m的梯子，斜立在一竖直的墙上，这时梯子底端距墙底端0.7m，如果梯子的顶端沿墙下滑0.4m，那么梯子底端将滑动

A.0.9m　　 B.1.5m　　 C.0.5m　　 D.0.8m

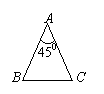11．如图，在下列三角形中，若AB＝AC，则能被一条直线分成两个小等腰三角形的是

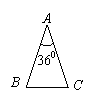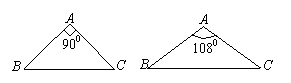（1）　　　　　 （2）　　　　　　  （3）　　　　　　  （4）

A.（1）（2）（3）　　　　　　　　　  B. （1）（2）（4）　　　　　　　

C.（2）（3）（4）　　　　　　　　　  D. （1）（3）（4）

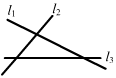12．如图，l₁、l₂、l₃表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有

A、一处　　 B、二处　　 C、三处　　 D、四处

二、填空题 （每题5分，共30分）

13．如图，已知AC=BD，∠A=∠D=90°，

要使得△ABC≌△DCB，只需增加的一个条件

是___________(填一个你认为正确的条件即可).

14．

15．如图，为了求出湖两岸A、B两点之间的距离，观测者

从测点A、B分别测得∠BAC＝90°，∠ABC＝30°，

又量得BC＝160 m，则A、B两点之间的

距离为　　m（结果保留根号）

16．在ΔABC中，如果只给出∠A=60°，那么要使这个三角形

是等边三角形，还需添加的条件是　　　　　  　　　　　 。

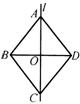17．如图，l是四边形ABCD的对称轴，如果AD∥BC，有下列结论：①AB∥CD； ②AB＝BC ；③AB⊥BC ；④AO＝OC。其中正确的结论是______________________________．（把你认为正确的结论的序号都填上）

18．等腰三角形一边上的高等于另一边的一半，则这个三角形

的顶角为________________。

三、解答题（共72分）

19．（本题满分8分）

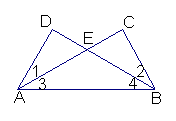如图，给出下列论断：①DE=CE，②∠1=∠2，③∠3=∠4。

请你将其中的两个作为条件，另一个作为结论，构成一个真命题，并加以证明。

20．（每题6分，共24分解方程）

（1）.（配方法解）　

（2）.（配方法解）

（3）.（公式法解）

（4）.（公式法解）

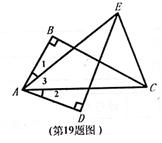
21．(本题8分)如图，∠1=∠2，AB=AD，∠B=∠D=90°，请判断△AEC的形状，并说明理由.

22．(本题6分)如图，△ABC中，AB=AC，∠A=36°.仿照图(1),请你设计两种不同的分法，将△ABC分割成3个三角形，使每个三角形都是等腰三角形(要求标出每个等腰三角形三个内角的度数).

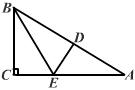23、(本题8分)如图，在Rt△ABC中，∠C=90°，沿过B点的一直线BE折叠这个三角形，使点C与AB边上的一点D重合。当∠A满足什么条件时，点D恰好为AB的中点？写出一个你认为适当的条件，并利用此条件证明D为AB的中点.

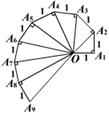
24．(本题8分)如图是第七届国际数学教育大会的会徽。它的主题图案是由一连串如图所示的直角三角形演化而成的。设其中的第一个直角三角形OA₁A₂是等腰三角形，且OA₁=A₁A₂=A₂A₃=A₃A₄=……=A₈A₉=1，请你先把图中其它8条线段的长计算出来，填在下面的表格中，然后再计算这8条线段的长的乘积。

OA1	OA2	OA3	OA4	OA5	OA6	OA7	OA8

25．（本题满分10分）

我们知道相交的两直线的交点个数是1，记两平行直线的交点个数是0；这样平面内的三条平行线它们的交点个数就是0，经过同一点的三直线它们的交点个数就是1；依次类推……

（1）请你画图说明同一平面内的五条直线最多有几个交点？

（2）平面内的五条直线可以有4个交点吗？如果有，请你画出符合条件的所有图形；如果没有，请说明理由．

（3）在平面内画出10条直线，使交点数恰好是31．