初三数学《整式的运算》复习

初三数学第二学期月考测试卷

（第Ⅰ卷）

一、选择题

1、　　　　 据测算，我国每天因土地沙漠化造成的经济损失为1.5亿元，若一年按365天计算，用科学记数法表示我国一年因土地沙漠化造成的经济损失为　　　　　　　　　　　　　　　　　　 （　　　 ）
A、5.475×10¹¹（元）　　　　　　　　　　　　　　　　B、5.475×10¹⁰（元）
C、0.5475×10¹¹（元）　　　　　　　　　　　　　　　D、5.475×10⁸（元）

2、　　　　 如果a＜2，那么化简的结果为　　　　　　　　　　　　　　　　　　 （　　　 ）
A、4－a　　　　　　　　　　B、a　　　　　　　　　　　　　　C、－a　　　　　　　　　　　　　　 D、4+a

3、　　　　 已知：x^m=1，xⁿ=2（x≠0）则x^3m-2n的值等于　　　　　　　　　　　　　　　　　 （　　　 ）
A、－1　　　　　　　　　　　B、－3　　　　　　　　　　　　C、4　　　　　　　　　　　　　　　　 D、

4、　　　　 一家三人（父亲、母亲、女儿）准备参加旅游，甲旅行社告知：“父母买全票，女儿按半价优惠”，乙旅行社告知：“家庭旅游可按团体票计价，即每人按均价的　 收费”。若这两家旅行社每人的原票价相同，那么优惠条件是　　　　　　　　　　　 （　　　　）
A、甲比乙更优惠　　B、乙比甲更优惠　　　C、甲与乙相同　　　　 D、与原票价有关

5、　　　　 如图：天平右盘中每个砝码的重量都是1g，则图中显示出某药A的重量范围是
　　 　　　　　　　　　　　　　　　　　　　　　　　 （　　　　）　　　　　　　　　
　 A、大于2g　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B、小于3g　
　 C、大于2g且小于3g　　　　　　　　　　　　　　　　　　　　　　　　D、大于2g或小于3g

6、　　　　 圆心都在y轴上的两圆相交于A，B两点，如果A点坐标为（2，），那么B点的坐标是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　　）
A、（2，）　　　 B、（—2，）　　　 C、（—2，）　　　　　 D、（2，）

7、　　　　 在函数y=中，自变量x的取值范围是　　　　　　　　　　　　　　　　　 （　　　　）
A、X≠0　　　　　　　　　 B、X≥—2　　　　　　　　　　C、X≥—2且x≠0　　　 D、X＞—2

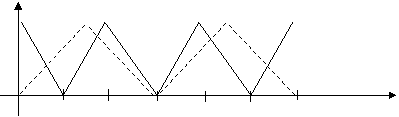
8、　　　　

距离（米）

90

（秒）

180

150

120

90

60

30

一游泳池长90米，甲、乙二人分别在游泳池相对两边同时朝另一边游泳，甲的速度是3米/秒，乙的速度是2米/秒，图中的实线和虚线分别表示甲、乙与游泳池一边的距离随游泳时间的变化而变化的图像，若不考虑转向时间，则从开始起到3分钟止他们相遇的次数为　　　　　　　（　　　 ）
A、2次　　　　　　　　　　　　B、3次　　　　　　　　　　　 C、4次　　　　　　　　　　　　　D、5次

9、　　　　 若点（x₁，y₁），（x₂，y₂），（x₃，y₃）都是反比例函数y=图象上的点，并且　　　　 x₁＜0＜x₂＜x₃，则下列各式中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　 ）
A、y₁＜y₂＜y₃　　　　　　　B、y₂＜y₃＜y₁ C、y₃＜y₂＜y₁D、y₁＜y₃＜ y₂

10、　　 一段导线，在0℃时的电阻为2欧，温度每升高1℃，电阻增加0.008欧，那么电阻R欧表示为温度t℃的函数关系式为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　 ）
A、R=0.008t　　　　　　　　B、R=2+0.008t　　　　　 C、R=2.008t　　　　　　　 D、R=2 t+0.008

11、　　 下列图形是轴对称图形而不是中心对称图形的是　　　　　　　　　　　　　　　　（　　　 ）
A、平行四边形　　　　　 B、菱形　　　　　　　　　　　C、正方形　　　　　　　　 D、等腰梯形

12、　　 下列命题的真命题有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　 ）
（1）两组对角分别相等的四边形是平行四边形
（2）平分弦的直径垂直弦
（3）到定点距离等于定长的点的轨迹是以定点为圆心，定长为半径的圆
（4）用正五边形可以进行平面镶嵌
A、1个　　　　　　　　　　　　B、2个　　　　　　　　　　　 C、3个　　　　　　　　　　　D、4个

13、　　 轮船航行到C处时，观测小岛B的方向是北偏西35°，那么同时从B观测到轮船的方向是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　 ）
A、南偏西35°　　　　　B、北偏西35°　　　　 C、南偏东35°　　　　D、南偏东55°

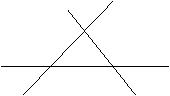
14、　　 如图，直线l₁，l₂，l₃表示三条相互交叉的公路，要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　 ）
　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 A、一处　　　　　　　　　　B、两处
　　　　　　　　　　　　　　　　　  C、三处　　　　　 D、四处
　　　　　　 　 

15、　　

L1

L3

L2

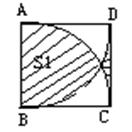
如图，正方形ABCD的边长为1，分别以A、B为圆心，1为半径作弧，则图中两块阴影部分的面积差（S₁-S₂）的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　　）　

　　　　　　　  S2

A、　　B、　　　C、　　  D、
　　　　　　　　　　　　　　　　　　　　　　　　　
（第Ⅱ卷）

二、填空题

16、　　 分解图式：4x²-y²-4x+1=　　 　　　　　　　　　　　　 。

17、　　 若a＜0，ab＜0，化简=　　　　　　　　　　　　 。

18、　　 若关于x的方程4x²+4kx+k²=0的一个根是—2，则k =　　　　　　　 。

19、　　 某工厂把500万元的资金投入到新产品生产，第一年获得了一定的利润，在不抽掉资金和利润（即将第一年获得的利润也作为生产资金）的情况下，继续生产。第二年的利润率（即所获利润与投入生产资金的比）比第一年的利润率增加了8%，如果第二年利润为112万元，为求第一年的利润率，可设它为x，那么所列方程为　　　　　　　　　　　　　　 。

20、　　 如图，要把边长为6的正三角形硬纸板剪去三个角，得到正六边形，它的边长为
　　　　　　  。

　　　　　　　　　　　　　　　　　　　　　　 

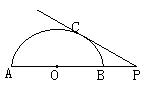
21、　　 已知：如图，AB是半圆O的直径，P是AB延长线上一点，PC切半圆O于点C，若，则∠P的度数为　　　　  。　　

三、解下列各题

22、　　 化简：

23、　　 已知：关于x的方程x²-2(m+1)x+m²-3=0
（1）当m取何值时，方程有两个不相等的实数根。
（2）设方程的两个实根分别为x₁，x₂，当（x₁+ x₂）²—（x₁+ x₂）—12=0时，求m的值。

24、　　 某家庭搬进新居后又添置了新的电冰箱、电热水器等家用电器，为了了解用电量的大小，该家庭在六月初连续几天观察电表的度数，电表显示的度数如下表所示：

日期	1日	2日	3日	4日	5日	6日	7日	8日
电表显示度数(度)	115	118	122	127	133	136	140	143

请你估计这个家庭六月份的总用电量是多少度？

 

　　　　　　　 

四、　　　　　　　　　　　　　　　　　　　　　 

25、　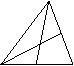　  在△ABC中，D为BC边中点，E为AC边上的任意一点，BE交AD于点O，某学生在研究这一问题时，发现了如下的事实：　　　A
（1）当时，有　　　　 o　E　 （a）

　　　　　　　　　　　　　　　  　　图（a）  B　　 D　 C

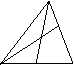A
（2）当时，有　　　　　  o　 E　　　(b)

　　　　　　　　　　　　　　　　　　 图（b）　B　　D　　C

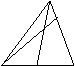A
（3）当时，有　　　　　　  o　　　　  ( c )

图（c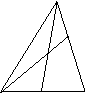）　B　　D　　C　　　　　　  A
猜想：当，　　　　　　　　 ；请证明你的猜想。　　　　　　  E

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　B　　 D　　 C

五、

26、某自行车保管站在某个星期日接受保管的自行车共3500辆次，其中变速自行车保管费是每辆次0.5元，一般车保管费是每辆每次0.3元。
（1）若设一般车停放的辆次数为x，总的保管费为y元，试写出y关于x的函数关系式；

（2）若估计前来停放的3500辆次中，变速车的辆次不小于25%，但不大于40%，试求该保管站这个星期日收入保管费总数的范围。

六、

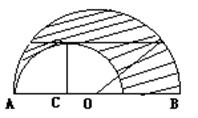
27、如图，在两个半圆中，大圆的弦MN与小圆相切，D为切点，且NM∥AB，MN=a，ON，CD
分别为两圆的半径，求阴影部分的面积。
　　　　　　　　　　　　　　　　　　　　　　　　　 

八、

28、　　　  某人在公路上由A到B向东行走，在A处测得公路旁的建筑物C在北偏东60°方向，到达B处后，又测得建筑物C在北偏东45°方向，继续前时，若此人在行走过程中离建筑物C的最近距离为，求A、B之间的距离。