福州市2001年初中毕业班质量检查
数 学 试 卷
(完卷时间120分钟;满分150分)
一、填空(每小题3分,共36分)
1.3的相反数与–2的绝对值的和是_______________.
2.函数![]() 的自变量的取值范围是_______________.
的自变量的取值范围是_______________.
3.纳米是一种长度单位,1纳米为1毫米的百万分之一,用科学记数法表示:72纳米=_________毫米。
4.若最简二次根式![]() 与
与![]() 是同类二次根式,则
是同类二次根式,则![]() =________。
=________。
5.分解因式:![]() _______________.
_______________.
6.以![]() 两根的一元二次方程是_______________.
两根的一元二次方程是_______________.
7.五边形的内角是_______度.
 8.已知圆锥的底面半径为6cm,高为8cm,则圆锥的侧面积是_____
8.已知圆锥的底面半径为6cm,高为8cm,则圆锥的侧面积是_____![]() .
.
9.如图,ABCD中,AE平分∠DAB交CD于E,AB=5cm,BC=3cm,则CE=_______cm.
10.两圆的底面半径为4cm和6cm,圆心距为2cm,则两圆的公切线有_______条。
11.当m________时,方程![]() 有两个不相等的实数根。
有两个不相等的实数根。
12.数形结合思想、转化思想、分类讨论思想等是重要的数学思想,下列解题过程:已知:![]() 是方程
是方程![]() 的两个根。
的两个根。
求![]() 的值。
的值。
解:由根与系数关系,得![]()
![]() =
=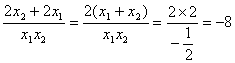 。主要应用了______________的思想。
。主要应用了______________的思想。
二、选择题(每小题4分,共32分,每小题都有A、B、C、D四个选项,其中只有一个选项是正确的,请把正确选项的代号写在题末的括号内)
1.已知![]() 是实数,下列式子中正确的是(
)
是实数,下列式子中正确的是(
)
A.3![]() >2
>2![]() B.
B. ![]() >
>![]() C.
C. ![]() ≥0 D.
≥0 D. ![]()
2.下列计算,正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.下列图形:等边三角形、等腰梯形、平行四边形、菱形、圆中,既是轴对称图形,又是中心对称图形的共有( )
A.4个 B.3个 C.2个 D.1个
4.下列命题中,真命题是( )
A.过三点可以作一个,并且只能作一个圆
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.平分弦的直径垂直平分连心线
D.圆内接四边形对角互补,并且任何一个外角都等于它的内对角
 5.如图,PA切⊙O于A,OP交⊙O于B,PA=4,PB=2,则⊙O半径是( )
5.如图,PA切⊙O于A,OP交⊙O于B,PA=4,PB=2,则⊙O半径是( )
A.6 B.4 C.3 D. 2
6.已知反比例函数![]() 的图象经过点A
的图象经过点A![]() 、B
、B![]() ,则
,则![]() 、
、![]() 之间的关系是( )
之间的关系是( )
A.m=n B.m+n=0 C.m>n D.m<n
 7.如图,∠ABC=∠CDB=90°,AC=
7.如图,∠ABC=∠CDB=90°,AC=![]() ,BC=
,BC=![]() ,要使ΔABC∽ΔCDB,那么BD与
,要使ΔABC∽ΔCDB,那么BD与![]() 、
、![]() 应满足(
)
应满足(
)
A.BD=![]() B.BD=
B.BD=![]() C.
C.![]() D.
D.![]()
 8.如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,若AD=DC,则sin∠ACO=( )
8.如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,若AD=DC,则sin∠ACO=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、(每小题7分,共28分)
1.先化简,再求值:
![]() ,其中
,其中![]() (结果精确到0.01,提供数据
(结果精确到0.01,提供数据![]() ≈1.414)
≈1.414)
 2.如图,梯形ABCD中,AD∥BC,AB=CD,E、F是BC上两点,BE=CF。
2.如图,梯形ABCD中,AD∥BC,AB=CD,E、F是BC上两点,BE=CF。
求证:AF=DE
3.解不等式,并把解集在数轴上表示出来。

 4.如图,四边形ABCD中,AB∥CD,AB=CD,AC、BD相交于点O,由这些条件,你能推出哪些结论?(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,写出4个结论即可,写在下面题号后)
4.如图,四边形ABCD中,AB∥CD,AB=CD,AC、BD相交于点O,由这些条件,你能推出哪些结论?(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,写出4个结论即可,写在下面题号后)
①
②
③
④
四、(10分)甲、乙两站相距300千米,火车提速后每小时快25千米,这样使得火车从甲站到乙站运行的时间缩短了1小时,求提速后火车从甲站到乙站需行驶多少小时?
五、(10分)为了考察某种大麦穗长的分布情况,在一块试验地里抽取20个穗,量得它们的长度如下(单位:cm)
7.0 6.6 6.8 7.0 7.2 7.4 7.0 7.3 7.5 7.4
7.3 7.1 7.0 6.9 6.7 7.1 7.2 7.0 6.9 7.1
若将数据分成5组,取组距为0.20cm
(1)补全下面频率分布表: (2)补全下面频率分布直方图

六、(10分)某地日用水量1万吨,每吨水价1元,为了更好地保护水资源,减少水污染,决定调整水价,将污水处理费计入水费,调查结果显示:水价调高的百分数为![]() 时,用水量减少的百分数为
时,用水量减少的百分数为![]()
(1)写出调价后该地日供水收入![]() (万元)与
(万元)与![]() 之间的函数关系式:
之间的函数关系式:
 (2)用配方法把(1)中函数关系式化为
(2)用配方法把(1)中函数关系式化为![]() 的形式,并求出
的形式,并求出![]() 取何值时,
取何值时,![]() 的值最大;
的值最大;
(3)调价后,当日供水收入最大时,该地每天节约用水多少吨?
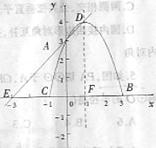
七、(12分)已知:一次函数与二次函数的图象如图所示:
(1)求这两个函数的解析式;
(2)抛物线上是否存在点P ,使得![]() ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。
 八、(12分)如图,在△ABC中,AB=AC=8,BC=10,点D、E分别在BC、AC边上(点D不与点B、C重合),且∠ADE=∠B,设BD=
八、(12分)如图,在△ABC中,AB=AC=8,BC=10,点D、E分别在BC、AC边上(点D不与点B、C重合),且∠ADE=∠B,设BD=![]() ,AE=
,AE=![]() 。
。
(1)求![]() 与
与![]() 之间的函数解析式,并写出函数的定义域;
之间的函数解析式,并写出函数的定义域;
(2)点D在BC上的运动过程中,△ADE是否有可能成为一个等腰三角形?如有可能,请求出当△ADE为等腰三角形时![]() 的值;如不可能,请说明理由。
的值;如不可能,请说明理由。
福州市2001年初中毕业班质量检查
数学试卷参考答案及评分标准
说明:
(一)考生的解法与“参考答案”不同时,可参照“答案”的评分标准的精神进行评分。
(二)以下解答各行右端所注分数表示正确做完该步应得的累计分数。
(三)评分最小单位是1分,得分或扣分都不出现小数。
一、(每小题3分,共36分)
1.
-1;2. ![]() ≥1且
≥1且![]() ≠2;3.
≠2;3. ![]() 4.1;5.(1+m-2n)(1-m+2n); 6.
4.1;5.(1+m-2n)(1-m+2n); 6. ![]() ; 7.540;8.60π; 9.2; 10.1; 11.>
; 7.540;8.60π; 9.2; 10.1; 11.>![]() ;12.转化
;12.转化
二、(每小题4分,共32分)
1.C; 2.B; 3.C; 4.D; 5.C; 6.B; 7.A; 8.A
三、(每小题7分,共28分)
1.解:原式![]()
![]()
![]()
注:当![]() 时,原式
时,原式![]() 只得4分
只得4分
2. 证明:(图略)∵梯形ABCD中AD∥BC,AB=CD
∴∠B=∠C![]()
∵BE=CF
∴BE+EF=CF+EF 即BF=CE![]()
∴ΔABF≌ΔDCE![]()
∴AF=DE![]()
3.解:不等式![]()
不等式![]() 的解集是
的解集是![]()
数轴图示(略)…………………………………………………………(6分)
∴原不等式组的解集是–1≤x<3
4.每写一个结论得2分,写对第4个结论再给1分
四、(10分)
解:设提速后火车从甲站到乙站需行驶![]() 小时
小时
据题意,得![]()
![]()
解得![]()
经检验:![]()
![]()
![]() 应舍去
应舍去![]()
 答:提速后火车从甲站到乙站需行驶3小时
答:提速后火车从甲站到乙站需行驶3小时![]()
五、(10分)
六、(10分)
解:(1)![]() (3分)
(3分)
(2)![]()
![]() (4分)
(4分)
![]() (5分)
(5分)
![]()
![]() (6分)
(6分)
当![]() (7分)
(7分)
(3)当![]() 时,
时,![]() (8分)
(8分)
![]() (吨)………………………(9分)
(吨)………………………(9分)
∴该地区每天节约用水100吨…………………………………………………(9分)
七、(12分)(图略)
解:(1)设一次函数的解析式为![]() 观察图象,知其过点(-3,0)和(0,3),利用待定系数法,可解得
观察图象,知其过点(-3,0)和(0,3),利用待定系数法,可解得![]() ∴一次函数的解析式为
∴一次函数的解析式为![]() (2分)
(2分)
设二次函数的解析式为![]()
据图象,其经过点C(–10,)、B(3,0)、A(0,3)列方程组可解得![]() –1,
–1,![]() ,
,![]()
∴![]() (5分)
(5分)
(2)存在
解:设ΔAOE中AE边上高为![]() ,ΔPAD中AD边上高为
,ΔPAD中AD边上高为![]() ,
,
∵![]()
∴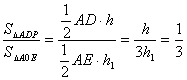 ∴
∴![]() (8分)
(8分)
与直线DE距离为![]() 的点在与DE平行且距离为
的点在与DE平行且距离为![]() 的直线上,符合条件的直线是
的直线上,符合条件的直线是![]() (9分)
(9分)
①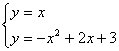 ②
②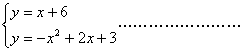 (10分)
(10分)
由①解得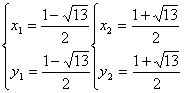 ②无解
②无解
∴存在点P,使![]() ,点P的坐标是
,点P的坐标是![]()
![]() (12分)
(12分)
八、(12分)
(1)解:∵AB=AC=8,∴∠B=∠C,∵∠ADE=∠B,∵∠ADC=∠B+∠BAD=∠ADE+∠EDC,∴∠EDC=∠BAD,∴ΔABD∽ΔDCE。…………………(3分)
∴CE:BD=CD:AB, ∴CE:![]() =(10-
=(10-![]() ):8,
):8,
![]() ∴
∴![]() (4分)
(4分)
定义域为![]() (5分)
(5分)
(2)证: ΔADE可能成为一个等腰三角形,
∵∠AED>∠C=∠ADE, ∴AE≠AD
(![]() )若AD=DE,则∵∠BAD=∠EDC, ∠B=∠C,
)若AD=DE,则∵∠BAD=∠EDC, ∠B=∠C,
∴ΔABD≌ΔDCE, (A·A·S) ![]() (7分)
(7分)
∴CD=AB=8,∴![]() =BD=2
=BD=2![]() (8分)
(8分)
![]() 若AE=DE,则∠EAD=∠ADE=∠B,
若AE=DE,则∠EAD=∠ADE=∠B,
ΔCAD∽ΔCBA,∴CD:CA=CA:CB,![]() (10分)
(10分)
∴(10-![]() ):8=8:10,∴
):8=8:10,∴![]()
∴ΔADE为等腰三角形时,![]() 的值为2或
的值为2或![]()
![]() (12分)
(12分)