初三数学月考试题
一、 选择题：（下列每小题所给的四个选项中，只有一个是正确的；将正确答案的代号填入题后的括号内；每小题3分，共20分）
1.方程（m+2）x「m」+(m-2)x+3=0是关于x的一元二次方程，则 （ ）
A m＝±2 B m＝2 C m＝－2 D m≠－2
2.在Rt△ABC中，∠C=90°，AC=6，BC=8，cosB等于（ ）
A B C D
3.方程x2=3x的根是 （ ）
A 0 B 3 C 0，3 D 0，-3
4.如果tan20°*tanα=1，则α等于 （ ）
A 20° B 70 ° C 80 ° D160°
5. 一元二次方程x2 -（2m+1）x-3=0的根的情况 （ ）
A 有两个不相等的实数根 B 有两个相等的实数根
C 没有实数根 D由m的取值来确定
6.若＜α＜，则α取值范围是 （ ）
A0°＜α＜30°B30°＜α＜60°C60°＜α＜90° D30°＜α＜90°
7.矩形的长和宽分别是方程x2 -6x+4=0的两个根，则这个矩形的面积是 （ ）
A 3 B 6 C 12 D 4
8.斜坡AB的坡度I=1/，则坡角α为 （ ）
A 30 ° B 45° C 60 ° D 75°
9.在△ABC中，AB=AC=10，BC=16，则tan等于 （ ）
A B C D
10.设“▲”“■”“●”表示三种不同的物体，现用天平秤了两次，情况如图所示，那么“▲”“■”“●”这三种物体的质量按照从大到小的顺序是 （ ）
A ▲ ● ■ B■ ▲ ●
■ ●
C ■ ● ▲ D● ■ ▲
△
■ ■
▲▲▲
●▲
△
二、 填空题：（每空3分，共30分）
11.方程2x-3=x(2x-3)的解是___________________.
12.在Rt△ABC中，∠C=90°，若AC=3BC，则tanB=_______.
13.mx2-x+3=0有两个实数根，则m的取值范围是_____________.
14.在△ABC中，∠A,∠B 满足 2sinA-1 +=0,则∠C=______度。
15.以1+，1-为根的一元二次方程是_____________________.
16.如果∠A是锐角，且sinA是方程2x2-5x+2=0的一个根则sinA=_____________。
17.已知(x2+y2) (x2+y2-1)=6,则x2+y2 =_____________
18.如果n是方程 x2+mx+n=0的根，n≠0，则m+n=____________
19.有一物体发射出去，到达最高点时与发射点成60°角，且此时高度为10米，则此时它离开发射点的水平距离是__________米。
20.观察下列图形
 | |||
 | |||
 |  |  |
从这三个图形中找出小正方形的个数与层数间的关系规律，猜出第n个图形中，小正方形的个数y与层数n间的关系__________________.
三、 解答题：（共40分）
21.解下列方程（每小题5分，共10分）
⑴ 2x2+7x=4 ⑵ 3x(x+2)=5(x+2)
22.如图在Rt△ABC中，∠C=90°b=8,∠A的平分线长AD=
求：∠B及c的值
B
D
A
C
23.已知关于x的方程2x2-(4k+1)x+2k2-1=0当为何值时原方程
⑴ 有两个相等的实数根
⑵有两个不相等的实数根
⑶无实数根 (6分)
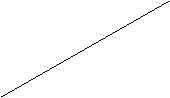
24.如图，河岸边有水塔AB，测量人员在河对岸C处测得塔顶A的仰角为30°，然后沿着CB方向前进20米到达D处又测得塔顶A的仰角为45°，请根据上述数据计算水塔的高。（精确到0.1米，=1.732）
A
C
D
B
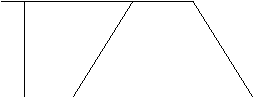
25.如图，在某公路路基横断面为等腰梯形，该工程设计要求路面宽度为10米，坡角为55°，路基高度为5.8米求路基下底宽。（精确到0.1米，cot55°0.7002）(6分)
10m
 | |||
 | |||
5.8m
55°
26.已知△ABC中，∠C=90°，且 sinA与sinB是关于 x的方程4x2-2(m+1)x+m=0的两个根，求m的值。 （6分）
（B卷 50分）
27.已知关于x的方程3xa2-a-4-2ax-a=0与关于y的方程5yb2-2b-1-by-b=0都是一元二次方程，且a≠b
求 a2-3ab+2b2的值 （8分）
28.求值。（每小题5分，共10分）
(1)(3tan18°)20(tan72°)20
(2)sin244°+sin245°+sin246°
29.已知α是锐角，且tanα是关于x的方程x2-2x-3=0的一个根
求
3sinα-5cosα的值
4cosα-3sinα (8分)
30.已知m是方程2x2+3x-1=0的根
求 4m2+6m的值 (8分)
31.已知Rt△ABC中，∠C=90°，周长是2+，斜边上的中线为1，求 tanA+tanB的值 （8分）
32.根据解直角三角形的知识，设计一个测量校园内旗杆高度的图形，写出需要测量的数据，并写出计算的式子。 （8分）