四川省泸州市2005年初中毕业考试暨高中阶段学习招生统一考试
(非课改县区)
数学试卷
(考试时间:只完成A卷120分钟,完成A、B卷150分钟)
说明:
1.本次考试试卷分为A、B卷,只参加毕业考试的考生只需完成A卷,要参加升学考试的考生必须加试B卷.
2.A卷分为第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷(1至2页)为选择题,第Ⅱ卷(3至6页)为非选择题,满分为100分.B卷(7至10页)为非选择题,满分为50分.A、B卷满分为150分.
A卷
第Ⅰ卷 选择题(共60分)
注意事项:
1.第Ⅰ卷共2页,答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目填写在答题卡上.考试结束后,监考人员将试卷和答题卡一并收回.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后再选涂其它答案,不能答在试卷上.
一、选择题(共60分,每小题3分)
以下每小题给出的四个选项中,只有一个是符合题目要求的,请选出并把答题卡上对应题目的正确答案标号涂黑.
1.在-2,0,![]() ,1,
,1,![]() ,-0.4中,正确的个数为
,-0.4中,正确的个数为
A.2个 B.3个 C.4个 D.5个
2.3的倒数为
A.-3 B.3 C.![]() D.
D.![]()
3.计算![]() 的结果为
的结果为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.现在我市人口约有人,用科学记数法表示为
A.458×104 B.45.8×105 C.4.58×106 D.0.458×107
5.函数![]() 中,自变量
中,自变量![]() 的取值范围为
的取值范围为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.不等式2x≥x+2的解集为
A. x>2 B. x<2 C.x≥2 D.x≤2
7.把![]() 分解因式为
分解因式为
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.下列图形中,是中心对称图形的是
A.等边三角形 B.平行四边形 C.梯形 D.正五边形
9.某装修公司到科维商场买同样一种多边形的地砖平铺地面,在以下四种地砖中,你认为该公司不能买
![]()
![]()
 A.正三角形地砖 B.正方形地砖 C.正五边形地砖 D.正六边形地砖
A.正三角形地砖 B.正方形地砖 C.正五边形地砖 D.正六边形地砖
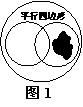
10.在学习“四边形”一章时,小明的书上有一图因不小心被滴
上墨水(如图1),看不清所印的字,请问被墨迹遮盖了的文字应是
A.等边三角形 B.四边形
C.等腰梯形 D.菱形
11.已知P(-1,2),则点P所在的象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.用换元法解方程![]() ,若设
,若设![]() ,则原方程可变形为
,则原方程可变形为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.两圆的半径分别是4cm和5cm,圆心矩为9cm,则两圆的位置关系是
A.外切 B.内切 C.外离 D.内含
14.一位卖“运动鞋”的经销商到一所学校对9位学生的鞋号进行了抽样调查. 其号码为:24、22、21、24、23、20、24、23、24. 经销商最感兴趣的是这组数据中的
A.中位数 B.众数 C.平均数 D.方差
15.下列方程中,没有实数根的是
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
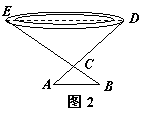
16.如图2,为了测量一池塘的宽DE,在岸边找到一点C,测
得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A
作AB∥DE交EC的延长线于B,测出AB=6m,则池塘的宽DE为
 A.25m B.30m
A.25m B.30m
C.36m D.40m
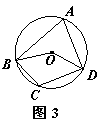
17.如图3,四边形ABCD为⊙O的内接四边形,
∠BOD=120°,则∠BCD为
A.120° B.90°
C.60° D.30°
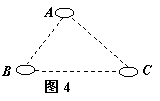 18.如图4,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在
18.如图4,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在
A.在AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边垂直平分线的交点处
D.在∠A、∠B两内角平分线的交点处
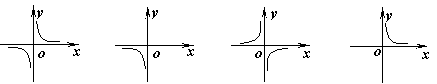 19.已知一个矩形的面积为24cm2,其长为ycm,宽为xcm,则y与x之间的函数关系的图象大致是
19.已知一个矩形的面积为24cm2,其长为ycm,宽为xcm,则y与x之间的函数关系的图象大致是
A B C D
 20.如图5,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地. 根据图中数据,计算耕地的面积为
20.如图5,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地. 根据图中数据,计算耕地的面积为
A.600m2 B.551m2
C.550 m 2 D.500m2
泸州市二OO五年初中毕业考试暨高中阶段学习招生统一考试
(非课改县区)
数学试卷(A卷)
第Ⅱ卷 (选择题 共40分)
注意事项:
1.第Ⅱ卷共4页,用钢笔或圆珠笔直接答在试卷上.
2.答卷前将密封线内的项目填写清楚.
| 题 号 | 第Ⅰ卷 | 第Ⅱ卷 | 总 分 | 总分人 | 复查人 | |||
| 二 | 三 | 四 | 合计 | |||||
| 得 分 |
|
|
|
|
| |||
| 得分 | 评卷人 |
|
|
|
二、(本题共15分,每小题5分)
21.计算:![]() .
.
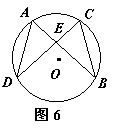 22.如图6,在⊙O中,弦AB与DC相交于E,且AE=EC,求证:AD=BC.
22.如图6,在⊙O中,弦AB与DC相交于E,且AE=EC,求证:AD=BC.
23.解方程组![]()
| 得分 | 评卷人 |
|
|
|
三、(本题共15分,第24题7分,第25题8分)
24.某篮球队在平时训练中,运动员甲的3分球命中率是70%,运动员乙的3分球命中率是50%. 在一场比赛中,甲投3分球4次,命中一次;乙投3分球4次,全部命中. 全场比赛即将结束,甲、乙两人所在球队还落后对方球队2分,但只有最后一次进攻机会了,若你是这个球队的教练,问:(1)最后一个3分球由甲、乙中谁来投,获胜的机会更大?(2)请简要说说你的理由.
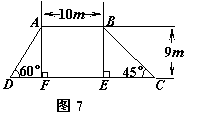 25.随着社会的发展,人们对防洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD,如图7所示,根据图中数据计算坝底CD的宽度(结果保留根号).
25.随着社会的发展,人们对防洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD,如图7所示,根据图中数据计算坝底CD的宽度(结果保留根号).
| 得分 | 评卷人 |
|
|
|
四、(本题10分)
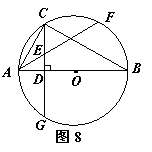 26.如图8,⊙O是△ABC的外接圆,AB为直径,AC=CF,CD⊥AB于D,且交⊙O于G,AF交CD于E.
26.如图8,⊙O是△ABC的外接圆,AB为直径,AC=CF,CD⊥AB于D,且交⊙O于G,AF交CD于E.
(1)求∠ACB的度数;
(2)求证:AE=CE;
(3)求证:AC2=AE•AF.
泸州市二0O五年初中毕业考试暨高中阶段学习招生统一考试
(非课改县区)
数学试卷(B卷)
注意事项:本卷共4页,用钢笔或圆珠笔直接答在试卷上.
| 题 号 | 一 | 二 | 三 | 四 | 总分 | 总分人 | 复查人 |
| 得 分 |
|
|
|
|
|
|
|
| 得分 | 评卷人 |
|
|
|
一、填空题(本题共15分,每小题3分)
1.已知∠![]() =32°,则它的余角= 度.
=32°,则它的余角= 度.
2.一个等腰三角形的两边分别为8cm和6cm,则它的周长为 cm.
3.若![]() 、
、![]() 为方程
为方程![]() 的两根,则
的两根,则![]() = .
= .
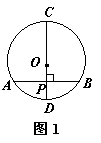 4.如图1,CD为⊙O的直径,弦AB⊥CD于P,PA=4cm,
4.如图1,CD为⊙O的直径,弦AB⊥CD于P,PA=4cm,
PD=2cm,则⊙O的直径为 cm.
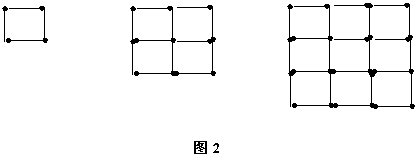
5.如图2是用火柴棍摆成边长分别是1、2、3根火柴棍时
的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火
柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).
 |
| 得分 | 评卷人 |
|
|
|
二、(本题共13分,第6题6分,第7题7分)
6.如图3,在□ABCD中,两条对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,以图中的任意四点(即点A、B、C、D、E、F、G、H、O中的任意四点)为顶点画两种不同的平等四边形.
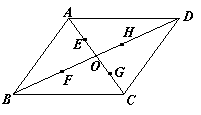 |  |
第一种: 第二种:
图3
7.为了确保我市国家级卫生城市的称号,市里对主要街道的排污水沟进行改造. 其中光明施工队承包了一段要开挖96米长的排污水沟,开工后每天比原计划多挖2米,结果提前4天完成任务,问原计划每天挖多少米?
| 得分 | 评卷人 |
|
|
|
三、(本题10分)
8.一天上行6点钟,汪老师从学校出发,乘车上市里开会,8点准时到会场,中午12点钟回到学校,他这一段时间内的行程S(km)(即离开学校的距离)与时间(h)的关系可用图4中的折线表示,根据图4提供的有关信息,解答下列问题:
(1)开会地点离学校多远?
(2)求出汪老师在返校途中路程S(km)与时间t(h)的函数关系式;
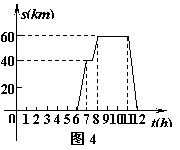 (3)请你用一段简短的话,对汪老师从上午6点到中午12点的活动情况进行描述.
(3)请你用一段简短的话,对汪老师从上午6点到中午12点的活动情况进行描述.
| 得分 | 评卷人 |
|
|
|
四、(本题12分)
9.如图5,抛物线![]() 与x轴、y轴分别相交于A(-1,0)、B(3,0)、C(0,3)三点,其顶点为D.注:抛物线
与x轴、y轴分别相交于A(-1,0)、B(3,0)、C(0,3)三点,其顶点为D.注:抛物线![]() 的顶点坐标为
的顶点坐标为![]() .
.
(1)求:经过A、B、C三点的抛物线的解析式;
(2)求四边形ABDC的面积;
(3)试判断△BCD与△COA是否相似?若相似写出证明过程;若不相似,请说明理由.
 |
泸州市二OO五年初中毕业考试暨高中阶段学习招生统一考试
(非课改县区)
数学试题参考答案及评分意见
说明:
1.如果考生的解法与下面提供的参考解答不同,凡正确的,一律记满分;若某一步出现错误,则可参照该题的评分意见进行评分.
2.评阅试卷,不要因解答中出现错误而中断对该题的评阅,当解答中某一步出现错误,影响了后继部分,但该步的解答未改变这一道题的内容和难度,在未发生新的错误前,可视影响的程度决定后面部分的记分,这时原则上不应超过后面部分应给分数之半;明显笔误,可酌情少扣;如有严重概念性错误,就不记分,在一道题解答过程中,对发生第二次错误起的部分,不记分.
3.涉及计算过程,允许合理省略非关键性步骤.
4.以下解答中右端所注分数,表示考生正确做到这一步应得的累加分数.
A卷
一、选择题(本题共60分,每小题3分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | B | D | D | C | B | C | D | B | C | D | B | C | A | B | A | C | A | C | D | B |
二、(本题共15分,每小题5分)
21.解:原式=![]() ………………(每化简正确一项给一分)3分
………………(每化简正确一项给一分)3分
=![]() ……………………………………………………5分
……………………………………………………5分
22.证明:在△AED和△CEB中
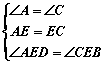 …………………………………………………………3分
…………………………………………………………3分
∴△AED≌△CEB……………………………………………………… 4分
∴AD=BC…………………………………………………………………5分
23.解:①+②,得
3x=15 ………………………………………………………………… 2分
∴ x=15 ………………………………………………………………3分
把x=5代入①,得y=2…………………………………………………4分
∴![]() 是原方程组的解…………………………………………………5分
是原方程组的解…………………………………………………5分
24.解法一:
(1)最后一个三分球由甲来投 ……………………………………………3分
(2)因甲在平时训练中3分球的命中率较高………………………………7分
解法二:
(1)最后一个3分球由乙来投 ……………………………………………3分
(2)因运动员乙在本场中3分球的命中率较高 …………………………7分
25.解:在Rt△ADF中,∠D=60°,![]() ……………………1分
……………………1分
∴DF=AF·cotD
=9×cot60°
=9×![]() ……………………………………………………3分
……………………………………………………3分
又在Rt△BEC中
∵∠C=45°, ∴△BEC为等腰三角形
∴EC=BE=9……………………………………………………………6分
在矩形AFEB中,FE=AB=10………………………………………7分
∴DC=DF+FE+EC
=![]()
=![]()
答:坝底DC的宽为![]() ………………………………………8分
………………………………………8分
26.(1)解:∵AB为⊙O的直径,∴∠ACB=90°……………………2分
(2)证明:∵AB为直径,且AB⊥CG
∴AC=AG………………………………………………………………3分
又∵AC=CF
∴AG=CF
∴∠ACG=∠CAF,∴AE=CE……………………………………6分
(3)连结CF,由(2)可知:AG=AC,∴∠ACE=∠AFC…………8分
又∵∠CAE=∠FAC,∴△AEC∽△ACF……………………………9分
∴![]()
∴AC2=AE·AF…………………………………………………………10分
B卷
一、填空题(本题共15分,每小题3分)
1.58 2.2或20 3.3 4.10 5.2n(n+1)
二、(本题共13分,第6题6分,第7题7分)
6.第一种:可画为□EFGH………………………………………………3分
第二种:可画为□DEBG………………………………………………6分
(或画为□AHCF)
7.解:设原计划每天挖x米,……………………………………………1分
由题意,得![]() ……………………………………………3分
……………………………………………3分
解之,得![]() ………………………………………………5分
………………………………………………5分
经检验,![]() 都是原方程的根,但工作效率为负数不合题意,
都是原方程的根,但工作效率为负数不合题意,
所以只取![]() …………………………………………………………6分
…………………………………………………………6分
答:原计划每天挖6米.…………………………………………… 7分
三、(本题10分)
8.解:(1)开会地点离学校有60千米……………………………………2分
(2)设汪老师在返校途中S与t的函数关系式为S=kt+b(k≠0).
由图可知,图象经过点(11,60)和点(12,0)
∴![]() ………………………………………………………4分
………………………………………………………4分
解之,得![]() ……………………………………………………5分
……………………………………………………5分
∴S=-60t+720(11≤t≤12)……………………………………7分
(3)汪老师由上午6点钟从学校出发,乘车到市里开会,到了40公里处时,发生了堵车,堵了约30分钟才通车,在8占钟准里到达会场开了3个小时的会,会议一结束就返校,结果在12点钟到校.………………………10分
(注:只要叙述合情合理都给全分)
四、(本题12分)
9.解:(1)由题意,得
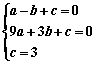 ………………………………………………………………2分
………………………………………………………………2分
解之,得![]()
∴![]() …………………………………………………………3分
…………………………………………………………3分
(2)由(1)可知![]()
∴顶点坐标为D(1,4)…………………………………………………4分
设其对称轴与x轴的交点为E
∵![]()
![]()
![]() ……………………………………………………………5分
……………………………………………………………5分
![]()
![]()
![]() …………………………………………………………6分
…………………………………………………………6分
![]()
![]()
![]() ……………………………………………………………7分
……………………………………………………………7分
![]()
![]()
![]() ………………………………………………………8分
………………………………………………………8分
(3)△DCB与△AOC相似………………………………………9分
证明:过点D作y轴的垂线,垂足为F
∵D(1,4)
∴Rt△DFC中,DC=![]() ,且∠DCF=45°
,且∠DCF=45°
在Rt△BOC中,∠OCB=45°,BC=![]()
∴∠AOC=∠DCB=90°……………………………………10分
![]() ………………………………………………11分
………………………………………………11分
∴△DCB∽△AOC……………………………………………12分
(注:其他解法只要过程和结果正确,仍给全分)