中考数学探索开放型测试题
1（大连）已知：如图1，给出下列6个论断，①AB是⊙O1的直径；②EC是⊙O1的切线；
③AC是⊙O2的直径；④BC·EC=DE·BD；⑤DE∥BC；⑥DE·BC=2CE2。
⑴将6个论断中的3个作为题设,2个论断作为结论，写出一个真命题，并加以证明；
⑵如果AB不是⊙O2直径(如图2)，你能否再从其余5 个论断中选取一个论断作为题设，一个论断作为结论，使其成为真命题(不要求证明)。若能，请写出两个；若不能，请你再添加一个条件，写出两个真命题。
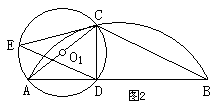
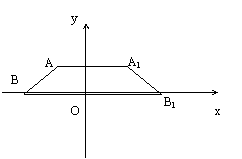
2（泉州）如图，在直角坐标系中，等腰梯形ABB1A1的对称轴为y轴。
（1）请画出：点A、B关于原点O的对称点A2 、B2（应保留画图痕迹，不必写画法，也不必证明）；
（2）连结A1A2、B1B2（其中A2、B2为（1）中所画的点），试证明：x轴垂直平分线段A1A2、B1B2；
（3）设线段AB两端点的坐标分别为A（-2 ，4）、B（-4 ，2），连结（1）中A2B2 ，试问在χ轴上是否存在点C ，使△A1B1C与△A2B2C的周长之和最小？或存在，求出点C的坐标（不必说明周长之和最小的理由）；若不存在，请说明理由。
解：
 |
3（广州）已知△ABC中，AC＝5，BC＝12，∠ACB＝90°，P是AB边上的动点（与点A、B不重合）Q是BC边上的动点（与点B、C不重合）．
（1）如图10，当PQ∥AC，且Q为BC的中点时，求线段CP的长；
（2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ
的长的取值范围；若不可能，请说明理由．
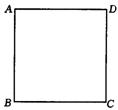
4（昆明）操作：如图8，在正方形ABCD中，P是CD上一动点（与C、D不重合），使三角尺的直角顶点与点P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E．
探究：（1）观察操作结果，哪一个三角形与△BPC相似？并证明你的结论；
（2）当点P位于CD的中点时，你找到的三角形与△BPC的周长比是多少
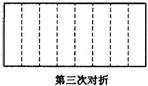
5（南宁）将一张长方形的纸对折，如图5所示可得到一条折痕（图中虚线）．续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折四次可以得到 条折痕．如果对折n次，可以得到 条折痕．
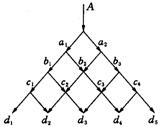
6（南宁）一条信息可通过如图7的网络线由上（A点）往下向各站点传送．例如信息到b2点可由经a1的站点送达，也可由经a2的站点送达，共有两条途径传送．则信息由A点到达山的不同途径共有（ ）．
（A）3条（B）4条（C）6条（D）12条
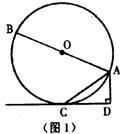
7（烟台）如图1，AB是⊙O的直径，AC是弦，直线CD切⊙O于点C．AD⊥CD，垂足为D．（1）求证：
＝AB·AD
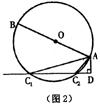
（2）若将直线CD向上平移，交⊙O于
、
两点，其它条件不变，可得到图2所示的图形，试探索A、A、AB、AD之间的关系，并说明理由．
（3）把直线D继续向上平移，使弦与直径AB相交（交点不与A、B重合），其它条件不变．请你在图3中画出变化后的图形，标好相应字母，并试着写出与（2）相应的结论，判断你的结论是否成立？若不成立，请说明理由；若成立，请给出证明．
8（陕西）如图，在直角坐标系中，以点A（
，0）为圆心，以
为半径的圆与x轴交于B、C两点，与y轴交于D、E两点．
⑴ 求D点的坐标；
⑵ 若B、C、D三点在抛物线
上，求这个抛物线的解析式；
⑶ 若⊙A的切线交x轴正半轴于点M，交y轴负半轴于点N，切点为P且∠OMN＝30°，试判断直线MN是否经过所求抛物线顶点？说明理由。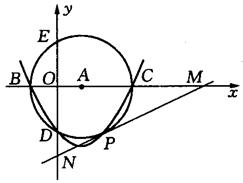
9（随州）已知，⊙O与直线l相切于点C，直径AB∥l，P是l上C点左边（不包括C点）一动点，AP交⊙O于D，BP交⊙O于E，DE的延长线交l于F．
（1）当PC＜AO时，如图1，线段PF与FC的大小关系是 。结合图1，证明你的结论．
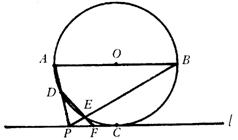
图1
（2）当 PC＞AO时，AP的反向延长线交⊙O于D，其它条件不变，如图2，（1）中所得结论是否仍然成立？
答：
。（不证明）
（3）如图2，当tan∠APB＝
，tan∠ABE＝
，AP＝
时，求PF的长．
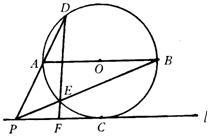
图2
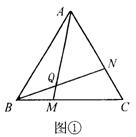
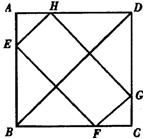
10（泰州）（1）已知△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM＝CN，直线BN与AM相交于Q点．就下面给出的三种情况（如图①、②、③），先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度？并利用图③证明你的结论．
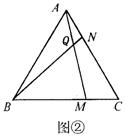
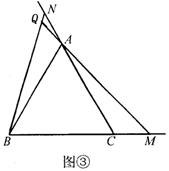
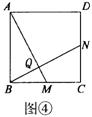
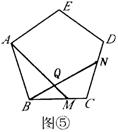
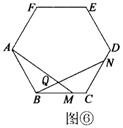
（2）将（1）中的“正△ABC”分别改为正方形ABCD（如图④）、正五边形ABCDE（如图⑤）。正六边形ABCDEF（如图③）、……、正n边形ABCD…X（如图（n）），“点N是射线CA上任意一点”改为点N是射线CD上任意一点，其余条件不变，根据（1）的求解思路，分别推断∠BQM各等于多少度，将结论填入下表：
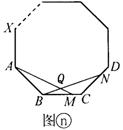
11（温州）为了美化校园环境，某中学准备在一块空地(如图，矩形ABCD，AB=10m，BC=20m)上进行绿化．中间的一块(图中四边形EFGH)上种花，其他的四块(图中的四个Rt△)上铺设草坪，并要求AE=AH=CF=CG．那么在满足上述条件的所有设计中，是否存在一种设计，使得四边形EFGH(中间种花的一块)面积最大?若存在，请求出该设计中AE的长和四边形EFGH的面积；若不存在，请说明理由．
12（武汉）已知：二次函数
的图像与x轴交于A（
，0）、B（
，0），＜0＜，与y轴交于点C，且满足
⑴ 求这个二次函数的解析式；（5分）
⑵ 是否存在着直线y＝kx＋b与抛物线交于点P、Q，使y轴平分△CPQ的面积？若存在，求出k、b应满足的条件；若不存在，请说明理由．（5分）
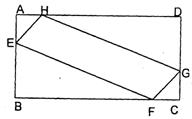
13（新疆）已知：如图，正方形ABCD的周长为4a，四边形EFGH的四个顶点E、F、G、H分别在AB、BC、CD、DA上滑动，在滑动过程中，始终有EH∥BD∥FG，且EH＝FG，那么四边形EFGH的周长是否可求？若能求出，它的周长是多少？若不能求出，请说明理由．
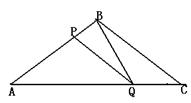
14(金华)如图所示，在ΔABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x。
（1）当x为何值时，PQ∥BC？
（2）当
，求
的值；（3）ΔAPQ能否与ΔCQB相似？若能，求出AP的长；若不能，请说明理由。
15（娄底）已知关于x的方程
.
(1) 求证：无论k取什么实数值，这个方程总有实数根；
（2）能否找到一个实数k，使方程的两实数根互为相反数？若能找到，求出k的值；若不能，请说明理由。
（3）当等腰三角形ABC的边长a=4，另两边的长b、c恰好是这个方程的两根时，求△ABC的周长。
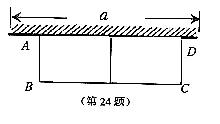
16（舟山）如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米，面积为S米2，
（1）求S与x的函数关系式
（2）如果要围成面积为45米2的花圃，AB的长是多少米？
（3）能围成面积比45米2更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由。
17（镇江）已知，如图，Rt△ABC中，∠ACB=900，AB=5，两直角边AC、BC的长是关于x的方程
的两个实数根。
（1）求m的值及AC、BC的长（BC>AC）
（2）在线段BC的延长线上是否存在点D，使得以D、A、C为顶点的三角形与△ABC相似？若存在，求出CD的长；若不存在，请说明理由。
18（辽宁）（1）如图（a），已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F（不与B重合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连结AC、AD．
求证：①∠BAD＝∠CAG；②AC·AD＝AE·AF．
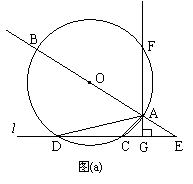
（2）在问题（1）中，当直线l向上平行移动，与⊙O相切时，其他条件不变．
①请你在图（b）中画出变化后的图形，并对照图（a），标记字母；
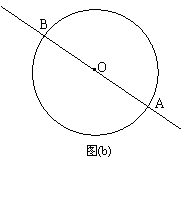②问题（1）中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．