初三数学第一学期夜课甲班练习（9） 姓名：____________
1．如图4，在□ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则线段BE，EC的长度分别为
A．2和3 B．3和2
C．4和1 D．1和4
2．如图5，现有一圆心角为90°，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为
A．4cm B．3cm
C．2cm D．1cm
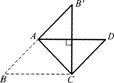
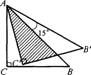3.如图，将等腰直角三角形ABc绕点A逆时针旋转15°后得到△AB’C’，若AC=1，则图中阴影部分的面积为( )．
(A)
/3
(B)/6
(c)
(D)3
4．小宇同学在一次手工制作活动中，先把一张矩形纸片按图5—1的方式进行折叠，使折痕的左侧部分比右侧部分短1cm；展开后按图5—2的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长1cm，再展开后，在纸上形成的两条折痕之间的距离是
A．0.5cm B．1cm C．1.5cm D．2cm
5.已知下列命题
①若
=m-1，则m≥1 ②平分弦的直径垂直于弦
③若a>b，则a+c>b+c ④若a>b，则a2>ab
其中原命题与逆命题均为真命题的个数是( )．(A)1个 (B)2个 (C)3个 (D)4个
6.若一元二次方程x2-2x-k=0无实数根，则二次函数y=x2+(k+1)x+k的图象的顶点在( )．
(A)第四象限 (B)第三象限 (C)第二象限 (D)第一象限
7．如右图，在梯形ABCD中，AD∥BC，∠B=90°，AD=1，AB=
，BC=2，P是BC边上的一个动点(点P与点B不重合)，DE⊥AP于点E。设AP=x，DE=y。在下列图象中，能正确反映y与x的函数关系的是
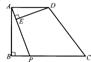
8.如图，已知在□ABCD中，AB=AC，如果沿对角线AC折叠后，使点B落在点B'处，并且恰好有B'C’⊥AD，则∠D= 度。
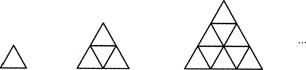
9.用长度相等的小木棒按下图的方式搭塔式三角形，按照这样的规律搭下去，搭第5个图形需要
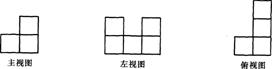10.下列图形是由一些相同的小正方体构成的几何体的三视图，这个几何体中相同的小正方体的个数有 个．
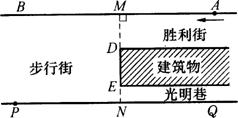
11．如图10所示，一段街道的两边缘所在直线分别为AB，PQ，并且AB∥PQ．建筑物的一端DE所在的直线MN⊥AB于点M，交PQ于点N．小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等候小亮．
（1）请你在图10中画出小亮恰好能看见小明时的视线，以及此时小亮所在位置（用点C标出）；
（2）已知：MN=20 m，MD=8 m，PN=24 m，求（1）中的点C到胜利街口的距离CM．
12． 观察下面的点阵图形和与之相对应的等式，探究其中的规律：
（1）请你在④和⑤后面的横线上分别写出相对应的等式：
 | |||||||||||
| |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
| |||||||||||
 | ||||||||
|
| |||||||
 | ||||||||
 | |||||
| |||||
 | |||||
| ||||
| ||||
（2）通过猜想，写出与第n个图形相对应的等式．
13． 探索，在图12—1至图12—3中，已知△ABC的面积为a ．
（1）如图12—1，延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S1，则S1=______（用含a的代数式
表示）；
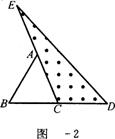
（2）如图12—2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S2，则S2=__________（用含a的代数式表示）；
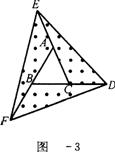（3）在图12—2的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图12—3）．若阴影部分的面积为S3，则S3=__________（用含a的代数式表示），并运用上述（2）的结论写出理由．
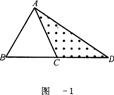
发现
像上面那样，将△ABC各边均顺次延长一倍，连结所得端点，得到△DEF（如图12—3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的 倍．
应用
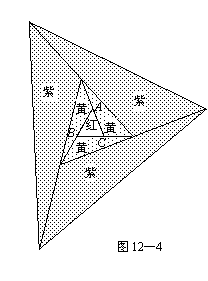要在一块足够大的空地上栽种花卉，工程人员进行了如下的图案设计：首先在△ABC的空地上种红花，然后将△ABC向外扩展三次（图12—4已给出了前两次扩展的图案）．在第一次扩展区域内种黄花，第二次扩展区域内种紫花，第三次扩展区域内种蓝花．如果种红花的区域（即△ABC）的面积是10平方米，请你运用上述结论求出：
（1）种紫花的区域的面积；
（2）种蓝花的区域的面积．
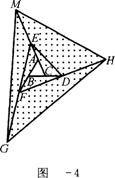
14．如图－1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．
（1）如图－2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；
（2）若三角尺GEF旋转到如图－3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．
15．利达经销店为某工厂代销一种建筑材料（这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理）．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7. 5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元．
设每吨材料售价为x（元），该经销店的月利润为y（元）．
（1）当每吨售价是240元时，计算此时的月销售量；
（2）求出y与x的二次函数关系式（不要求写出x的取值范围）；
（3）请把（2）中的二次函数配方成
的形式，并据此说明，该经销店要
获得最大月利润，售价应定为每吨多少元；
（4）小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．
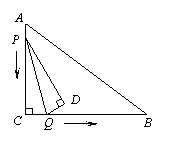
16．如图13，在Rt△ABC中，∠C＝90°，AC＝12，BC＝16，动点P从点A出发沿AC边向点C以每秒3个单位长的速度运动，动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动．P，Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ关于直线PQ对称的图形是△PDQ．设运动时间为t（秒）．
（1）设四边形PCQD的面积为y，求y与t的函数关系式；
（2）t为何值时，四边形PQBA是梯形？
（3）是否存在时刻t，使得PD∥AB？若存在，求出t的值；若不存在，请说明理由；
（4）通过观察、画图或折纸等方法，猜想是否存在时刻t，使得PD⊥AB？若存在，请估计t的值在括号中的哪个时间段内（0≤t≤1；1＜t≤2；2＜t≤3；3＜t≤4）；若不存在，请简要说明理由．
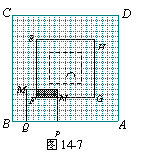
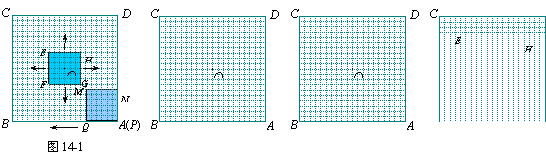
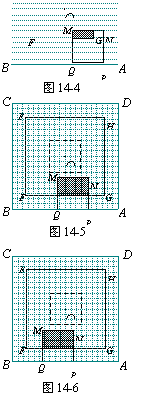
17．图14－1至图14－7的正方形霓虹灯广告牌ABCD都是20×20的等距网格（每个小方格的边长均为1个单位长），其对称中心为点O．
如图14－1，有一个边长为6个单位长的正方形EFGH的对称中心也是点O，它以每秒1个单位长的速度由起始位置向外扩大（即点O不动，正方形EFGH经过一秒由6×6扩大为8×8；再经过一秒，由8×8扩大为10×10；……），直到充满正方形ABCD，再以同样的速度逐步缩小到起始时的大小，然后一直不断地以同样速度再扩大、再缩小．
另有一个边长为6个单位长的正方形MNPQ从如图14－1所示的位置开始，以每秒1个单位长的速度，沿正方形ABCD的内侧边缘按A→B→C→D→A移动（即正方形MNPQ从点P与点A重合位置开始，先向左平移，当点Q与点B重合时，再向上平移，当点M与点C重合时，再向右平移，当点N与点D重合时，再向下平移，到达起始位置后仍继续按上述方式移动）．
正方形EFGH和正方形MNPQ从如图14－1的位置同时开始运动，设运动时间为x秒，它们的重叠部分面积为y个平方单位．
（1）请你在图14－2和图14－3中分别画出x为2秒、18秒时，正方形EFGH和正方形MNPQ的位置及重叠部分（重叠部分用阴影表示），并分别写出重叠部分的面积；
（2）①如图14－4，当1≤x≤3.5时，求y与x的函数关系式；
②如图14－5，当3.5≤x≤7时，求y与x的函数关系式；
③如图14－6，当7≤x≤10.5时，求y与x的函数关系式；
④如图14－7，当10.5≤x≤13时，求y与x的函数关系式．
（3）对于正方形MNPQ在正方形ABCD各边上移动一周的过程，请你根据重叠部分面积y的变化情况，指出y取得最大值和最小值时，相对应的x的取值情况，并指出最大值和最小值分别是多少．（说明：问题（3）是额外加分题，加分幅度为1～4分）
 | |||
| |||
| |||||||
 | |||||||
|
| ||||||
