初三数学第一学期夜课甲班练习(10) 姓名:____________
1.图1是测量一物体体积的过程:
步骤一,将![]() 的水装进一个容量为
的水装进一个容量为![]() 的杯子中.
的杯子中.
步骤二,将三个相同的玻璃球放入水中,结果水没有满.
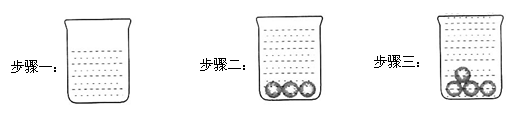 步骤三,同样的玻璃球再加一个放入水中,结果水满溢出.
步骤三,同样的玻璃球再加一个放入水中,结果水满溢出.
|
根据以上过程,推测一颗玻璃球的体积在下列哪一范围内?![]()
A.![]() 以上,
以上,![]() 以下 B.
以下 B.![]() 以上,
以上,![]() 以下
以下
C.![]() 以上,
以上,![]() 以下 D.
以下 D.![]() 以上,
以上,![]() 以下
以下
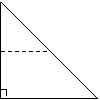
2.如图2(![]() ),在直角梯形
),在直角梯形![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发,由
点出发,由![]() 沿边运动,设点
沿边运动,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,如果关于
,如果关于![]() 的函数
的函数![]() 的图象如图2(
的图象如图2(![]() ),则
),则![]() 的面积为( )
的面积为( )
A.10 B.16 C.18 D.32
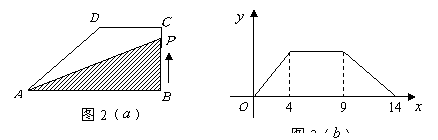
3.如图4,将一张等腰直角三角形纸片沿中位线剪开,可以拼出不同形状的四边形,请写出其中两个不同的四边形的名称: .
 4.如图5,在数轴上,A,B两点之间表示整数的点有 个.
4.如图5,在数轴上,A,B两点之间表示整数的点有 个.
 5.如图8是小明用火柴搭的1条、2条、3条“金鱼”
5.如图8是小明用火柴搭的1条、2条、3条“金鱼”![]() ,则搭
,则搭![]() 条“金鱼”需要火柴 根.
条“金鱼”需要火柴 根.

6.如图,依次连结第一个正方形各边的中点得到第二个正方形,再依次连结第二个正方形各边的中点得到第三个正方形,按此方法继续下去.若第一个正方形边长为1,则第![]() 个正方形的面积是_________________.
个正方形的面积是_________________.

7.两圆的半径分别是方程![]() 的两根,且圆心距d=7,则这两圆的位置关系 __.
的两根,且圆心距d=7,则这两圆的位置关系 __.
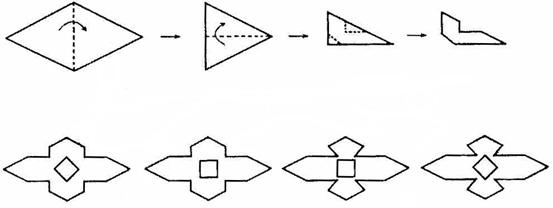
8.将一张菱形纸片,按下图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
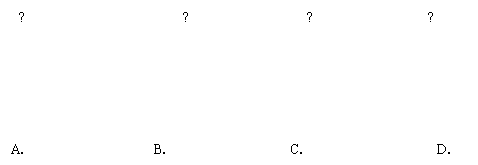
9.学友书店推出售书优惠方案:①一次性购书不超过100元,不享受优惠;②一次性购书超过100元但不超过200元一律打九折;③一次性购书200元一律打八折.如果王明同学一次性购书付款162元,那么王明所购书的原价一定为( )
A.180元 B . 202.5元 C. 180元或202.5元 D.180元或200元
 10.如图,在
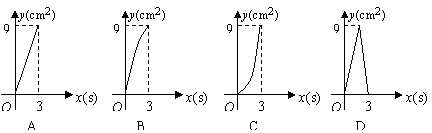
10.如图,在![]() 中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点Q从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPQ的面积
中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点Q从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPQ的面积![]() 与运动时间
与运动时间![]() 之间的函数图象大致是( )
之间的函数图象大致是( )
11.一个质地均匀的小正方体的六个面上分别标有数字1,2,3,4,5,6.如果任意抛掷小正方体两次,那么下列说法正确的是( )
A.得到的数字和必然是4 B.得到的数字和可能是3
C.得到的数字和不可能是2 D.得到的数字和有可能是1
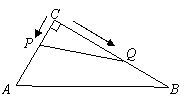
12.如图9,在相距60km的两个城镇A,B之间,有一近似圆形的湖泊,其半径为15km,圆心O恰好位于A,B连线的中点处.现要绕过湖泊从A城到B城,假设除湖泊外,所有的地方均可行走,如路线:线段AC→︵CD线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度.![]()

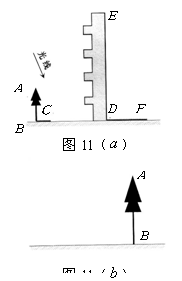
13.高为12米的教学楼![]() 前有一棵大树
前有一棵大树![]() ,如图11(
,如图11(![]() ).
).
(1)某一时刻测得大树![]() 、教学楼
、教学楼![]() 在阳光下的投影长分别是
在阳光下的投影长分别是![]() 米,
米,![]() 米,求大树
米,求大树![]() 的高度;
的高度;
(2)现有皮尺和高为![]() 米的测角仪,请你设计另一种测量大树
米的测角仪,请你设计另一种测量大树![]() 高度的方案,要求:
高度的方案,要求:
①在图11(![]() )中,画出你设计的测量方案示意图,并将应测量的数据标记在图上(长度用字母
)中,画出你设计的测量方案示意图,并将应测量的数据标记在图上(长度用字母![]() 表示,角度用希腊字母
表示,角度用希腊字母![]() 表示);
表示);
 ②根据你所画出的示意图和标注的数据,求出大树的高度(用字母表示).
②根据你所画出的示意图和标注的数据,求出大树的高度(用字母表示).
14.如图,在;△ABC中,AB=AC=5,以AB为直径的⊙P交BC于H.点A,B在x轴上,点H在y轴上,B点的坐标为![]() .
.
(1)求点A,H,C的坐标;
(2)过H点作AC的垂线交AC于E,交x轴于F,求证:EF是⊙P的切线.
(3)求经过![]() 两点且顶点到
两点且顶点到![]() 轴的距离等于4的抛物线解析式.
轴的距离等于4的抛物线解析式.
15.如图,在等腰梯形ABCD中,AB∥DC,∠A=45°,AB=10cm,CD=4cm.等腰直角三角形PMN的斜边MN=10cm,A点与N点重合,MN和AB在一条直线上,设等腰梯形ABCD不动,等腰直角三角形PMN沿AB所在直线以![]() 的速度向右移动,直到点N与点B重合为止.
的速度向右移动,直到点N与点B重合为止.
(1)等腰直角三角形![]() 在整个移动过程中与等腰梯形
在整个移动过程中与等腰梯形![]() 重叠部分的形状由
重叠部分的形状由
形变化为 形;
(2)设当等腰直角三角形PMN移动x(s)时,等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积为y(cm2),求y与x之间的函数关系式;
(3)当![]() 时,求等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积.
时,求等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积.
 |
16.阅读理解:
给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的2倍,则这个矩形是给定矩形的“加倍”矩形.如图12,矩形![]() 是矩形ABCD的“加倍”矩形.
是矩形ABCD的“加倍”矩形.
 |
请你解决下列问题:
(1)边长为a的正方形存在“加倍”正方形吗?如果存在,求出“加倍”正方形的边长;如果不存在,说明理由.
(2)当矩形的长和宽分别为m,n时,它是否存在“加倍”矩形?请作出判断,说明理由.
17.(本小题满分10分)
如图14(![]() ),两个不全等的等腰直角三角形
),两个不全等的等腰直角三角形![]() 和
和![]() 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点![]() .
.
(1)将图14(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角,在图14(
角,在图14(![]() )中作出旋转后的
)中作出旋转后的![]() (保留作图痕迹,不写作法,不证明).
(保留作图痕迹,不写作法,不证明).
(2)在图14(![]() )中,你发现线段
)中,你发现线段![]() ,
,![]() 的数量关系是 ,直线
的数量关系是 ,直线![]() ,
,![]() 相交成 度角.
相交成 度角.
(3)将图14(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转一个锐角,得到图14(
顺时针旋转一个锐角,得到图14(![]() ),这时(2)中的两个结论是否成立?作出判断并说明理由.若
),这时(2)中的两个结论是否成立?作出判断并说明理由.若![]() 绕点
绕点![]() 继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.

18.(本小题满分12分)
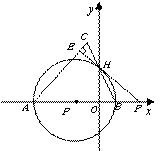
如图15,点![]() 在
在![]() 轴上,
轴上,![]() 交
交![]() 轴于
轴于![]() 两点,连结
两点,连结![]() 并延长交
并延长交![]() 于
于![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() 的半径为
的半径为![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求证:![]() 是
是![]() 的切线;
的切线;
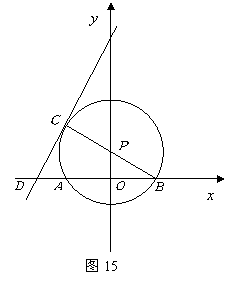 (3)若二次函数
(3)若二次函数![]() 的图象经过点
的图象经过点![]() ,求这个二次函数的解析式,并写出使二次函数值小于一次函数
,求这个二次函数的解析式,并写出使二次函数值小于一次函数![]() 值的
值的![]() 的取值范围.
的取值范围.
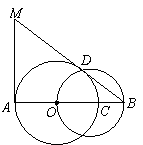
19.如图,点O是已知线段AB上一点,以OA为半径的⊙O交线段AB于点C,以线段OB为直径的圆与⊙O的一个交点为D,过点A作AB的垂线交BD的延长线于点M.
(1)求证:BD是⊙O的切线;
(2)若BC,BD的长度是关于x的方程![]() 的两个根,求⊙O的半径;
的两个根,求⊙O的半径;
(3)在上述条件下,求线段MD的长.
 |
20.如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线![]() 与
与![]() 轴的另一交点为A,顶点为P,且对称轴是直线
轴的另一交点为A,顶点为P,且对称轴是直线![]() .
.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在![]() 轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与
轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与![]() 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
相似,若存在,请求出点Q的坐标;若不存在,请说明理由.

