初中毕业数学学业（升学）、五年制专科招生考试
课改实验区数学科试题
特别提醒：
1．本卷为数学试题单，共27个题，满分150分，共4页．考试时间120分钟．
2．考试采用闭卷、用笔在特制答题卡上答题的答题形式，故不能在本题单上答题．
3．答题时请仔细阅读答题卡上的注意事项，并根据本题单各题的编号在答题卡上找到各题答题的对应位置，用规定的笔进行填涂和书写．
4．考试结束后，请将本题单与答题卡一并交回．
一、填空题（本大题共10小题，每小题3分，共30分）
请将各题横线上应填写的内容按题号顺序在答题卡中对应位置，用0.5毫米黑色签字笔填空．
1．
的倒数是
．
2．
的平方根是
．
3．如果点
和点
关于
轴对称，则
的值为
．
4．如果1，已知正方形
的边长为3，如果将线段
绕点
旋转后，点
落在
延长线上的
点处，那么
．
5．如果等腰三角形的两边长分别为4和7，则三角形的周长为 ．
6．如图2，把一张长方形纸条沿
折叠，若
，
则
．
7．某工厂生产了一批零件共1600件，从中任意抽取了80件进行检查，其中合格产品78件，其余不合格，则可估计这批零件中有
件不合格．
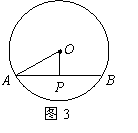
8．如图3，
的直径为26cm，弦
长为24cm，则点
到
的距离
为 ．
9．分解因式
．
10．观察下面一列数，按某种规律在横线上填上适当的数：
，则第
个数为
．
二、填空题（本大题共8小题，每小题4分，共32分）
每小题只有一项符合题意，请用2B铅笔在答题卡上规定的位置进行填涂．
11．我市今年参加中考人数约为
人，用科学记数法表示为（ ）
A．
B．
C．
D．
12．数轴上点表示
，点
表示1，则表示
两点间的距离的算式是（ ）
A．
B．
C．
D．
13．图4是由几个小立方块所搭成的几何体，那么这个几何体的主视图是（ ）
 |
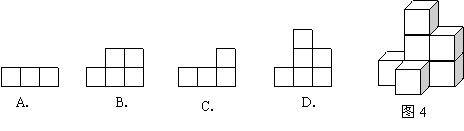14．根据图5和图6所示，对
三种物体的重量判断不正确的是（ ）
 |
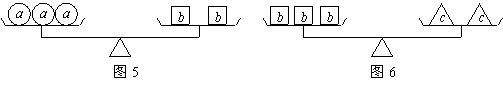A．
B．
C．
D．
15．下列运算正确的是（ ）
A．
B．
C．
D．
16．我市某一周的最高气温统计如下表：
| 最高气温（ | 25 | 26 | 27 | 28 |
| 天 数 | 1 | 1 | 2 | 3 |
）则这组数据的中位数与众数分别是（ ）
A．27，28 B．27.5，28 C．28，27 D．26.5，27
17．如图7所示，等腰梯形中，
，点
是
边的中点，
，则
等于（ ）
A．
B．
C．
D．
 |
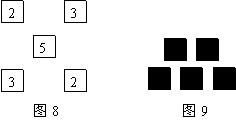
18．有5张写有数字的卡片（如图8所示），它们的背面都相同，现将它们背面朝上（如图9所示），从中翻开任意一张是数字2的概率（ ）
A．
B．
C．
D．
 |
三、解答题（本大题共9小题，共88分）
在答题卡上找到下列各题的对应位置，用0.5毫米黑色签字笔将解题过程答在答题卡上．
19．（本题满分8分）
计算：
20．（本题满分8分）
先化简，再求值：
，其中
21．（本题满分8分）
解不等式组：
22．（本题满分10分）
某校三个年级的初中在校学生共829名，学生的出生月份统计如下，根据图10中数据回答以下问题：
 |
（1）出生人数最少是几月？
（2）出生人数少于60人的月份有哪些？
（3）这些学生至少有两人生日在8月5日是不可能的、还是可能的、还是必然的？
（4）如果你随机地遇到这些学生中的一位，那么该学生生日在哪一个月的概率最大？
23．（本题满分10分）
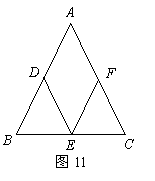
已知：如图11所示，在
中，
分别是
边上的中点．
（1）求证：四边形
是菱形（6分）
（2）若
，求菱形的周长．（4分）
24．列方程（组）解应用题：（本题满分10分）
将一摞笔记本分给若干同学，每个同学6本，则剩下9本；每个同学8本，又差了3本，问共有多少本笔记本、多少个同学？
25．（本题满分10分）
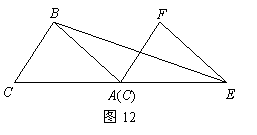
如图12，已知的面积为3，且
，现将
沿
方向平移的长度得到
．
（1）求所扫过的图形面积．（5分）
（2）探究：
与
的位置关系，并说明理由．（5分）
26．（本题满分12分）
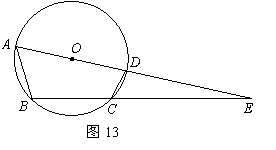如图13，
四点在上，
的延长线相交于点，直径
，且
（1）计算
（4分）
（2）计算
的值（4分）
（3）探究：的取值范围（4分）
27．（本题满分12分）
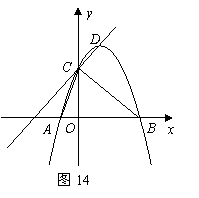如图14，已知二次函数
的图象与
轴交于点，点，与轴交于点，其顶点为
，直线
的函数关系式为
，又
．
（1）求二次函数的解析式和直线的函数关系式（8分）
（2）求的面积（4分）．