猜想、探索型专项训练A
总分120分，时间90分钟
一、细心填一填（每题3分，共30分）
1．（2006年海南）用同样规格的黑白两种颜色的正方形瓷砖按下图方式铺地板，则第（3）个图形中有黑色瓷砖 块，第
个图形中需要黑色瓷砖
块（用含的代数式表示）.
 |
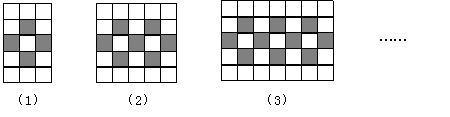2．（2006年南昌）用黑白两种颜色正方形的纸片按黑色纸片数逐渐加l的规律拼成一列图案：
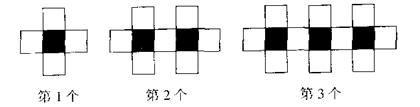
（1）第4个图案中有白色纸片 张
（2）第n个图案中有白色纸片 张
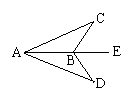
3．（2006年浙江）如图，点B在AE上，∠CAB=∠DAB，要使△ABC≌△ABD，可补充的一个条件是： (写出一个即可）．
4．（2006年泰州）如图，每个正方形点阵均被一直线分成两个三角形点阵，根据图中提供的信息，用含
的等式表示第个正方形点阵中的规律
．
 |
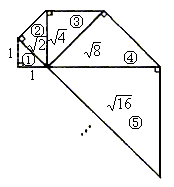
5．（2006年邵阳）图中的螺旋形由一系列等腰直角三角形组成，其序号依次为①、②、③、④、⑤……，则第n个等腰直角三角形的斜边长为_____________。
6．（2005年山东枣庄）100个数排成一行，其中任意三个相邻数中，中间一个数都等于它前后两个数的和，如果这100个数的前两个数依次为1，0，那么这100个数中“0”的个数为 ____________个．
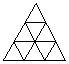
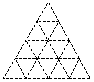
7．（2006年湖北荆门）如图,是用火柴棒摆出的一系列三角形图案,按这种方案摆下去,当每边上摆2006根火柴棒时,共需要摆________根火柴棒.
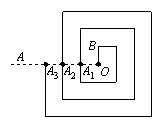
8．（2005年连云港）右图是一回形图，其回形通道的宽和
的长均为1， 回形线与射线
交于
…．若从
点到
点的回形线为第1圈（长为7），从点到
点的回形线为第2圈，…，依此类推．则第10圈的长为
．
9．（2006年广西贵港）观察下列各等式：
根据你发现的规律，计算：
（为正整数）
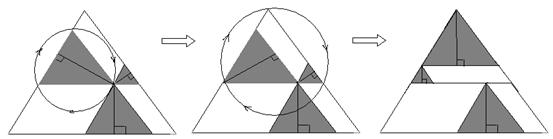
10．（2006年芜湖）请你仔细观察图中等边三角形图形的变换规律，写出你发现关于等边三角形内一点到三边距离的数学事实： 。
二、精心选一选（每题3分，共30分）
11．（2006年重庆市）按一定的规律排列的一列数依次为：
┅┅，按此规律排列下去，这列数中的第7个数是 （ ）.
A．
B．
C．
D．
12．（2006年荆州）用同样大小的正方形按下列规律摆放，将重叠部分涂上颜色，下面的图案中，第n个图案中正方形的个数是 （ ）
A． B．
C．
D．
13．根据下表中的规律，从左到右的空格中应依次填写的数字是
|
|
|
|
|
|
|
|
|
| 000 | 110 | 010 | 111 | 001 | 111 |
A．100，011 B．011，100 C．011，101 D．101，110
14．（2006年临安）已知：
、
、
、
，……，若 
（a、b为正整数）符合前面式子的规律，则a + b的值不可能是（ ）
A．109 B．218 C．326 D．436
15．（2006年泸州）木材加工厂堆放木料的方式如图9所示：依此规律可得出第6堆木料的根数是（ ）。
A．15 B．18 C．21 D．24
16．（2006年孝感）为迎接2008年北京奥运会，孝感市某中学课外科技小组的同学们设计制作了一个电动智能玩具，玩具中的四个动物小鱼、小羊、燕子和熊猫分别在1、2、3、4号位置上（如图），玩具的程序是：让四个动物按图中所示的规律变换位置，第一次上、下两排交换位置；第二次是在第一次换位后，再左、右两列交换位置；第三次再上、下两排交换位置；第四次再左、右两列交换位置；按这种规律，一直交换下去，那么第2008次交换位置后，熊猫所在位置的号码是 （ ）
A．1号 B．2号 C．3号 D．4号
17．（2005年南平）如右图，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依ABCDEFCGA的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断地爬行，直到行走2006cm后才停下来.请问这只蚂蚁停在那一个点？答：停在 点. （ ）
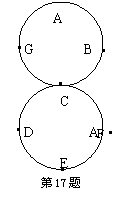
A．B点 B．D点 C．F点 D．E点
18．（2006年舟山）假定有一排蜂房，形状如图，一只蜜蜂在左下角，由于受了点伤，只能爬行，不能飞，而且始终向右方（包括右上、右下）爬行，从一间蜂房爬到右边相邻的蜂房中去.例如，密封爬到1号蜂房的爬法有：蜜蜂→1号；蜜蜂→0号→1号，共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有几种不同的爬法（ ）
A.7 B.8 C.9 D.10
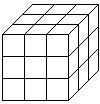19．（镇江市2005年） 一个正方体的表面涂满了颜色，按如图所示将它切成27个大小相等的小立方块，设其中仅有
个面（1，2，3）涂有颜色的小立方块的个数为
，则
、
、
之间的关系为（ ）
A．－＋＝1 B．＋－＝1
C．＋－＝2 D．－＋＝2
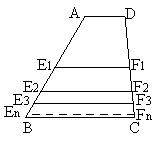
20．（2006年锦州）如图，在梯形ABCD中，AD∥BC，AD=a，BC=b.若E1、F1分别是AB、DC的中点，则
；若
、
分别是
、
的中点，则
；当
、
分别是
的中点，则
；若
、
分别是
、
的中点，根据上述规律猜想
＝____(n≥1，n为整数).
A. 
B.
C. 
D.
三、解答题（每题9分，共45分）
21．（2005年河南中考）观察下表，填表后再解答问题：
（1）试完成下列表格：
| 序号 | 1 | 2 | 3 | … |
| 图形 |
|
|
| … |
|
| 8 | 24 | … | |
|
| 1 | 4 | … |
(2)试求第几个图形中“
”的个数和“
”的个数相等？
22．（2006年福建南平）在下图中，每个正方形有边长为1 的小正方形组成：
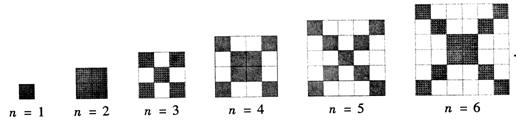（1）观察图形，请填写下列表格：
| 正方形边长 | 1 | 3 | 5 | 7 | … |
|
| 黑色小正方形个数 | … |
| 正方形边长 | 2 | 4 | 6 | 8 | … |
|
| 黑色小正方形个数 | … |
（2）在边长为（
）的正方形中，设黑色小正方形的个数为
，白色小正方形的个数为
，问是否存在偶数，使
？若存在，请写出的值；若不存在，请说明理由。
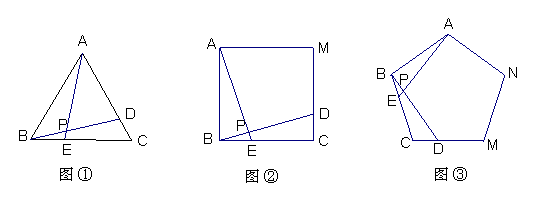
23．（2006年大连西岗）如图①、②、③中，点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点，且BE = CD，DB交AE于P点．
⑴求图①中，∠APD的度数；
⑵图②中，∠APD的度数为___________，图③中，∠APD的度数为___________；
⑶根据前面探索，你能否将本题推广到一般的正n 边形情况．若能，写出推广问题和结论；若不能，请说明理由．
24．（2006年贵阳）两条平行直线上各有个点，用这对点按如下的规则连接线段；
①平行线之间的点在连线段时，可以有共同的端点，但不能有其它交点；
②符合①要求的线段必须全部画出；
图1展示了当
时的情况，此时图中三角形的个数为0；
图2展示了当
时的一种情况，此时图中三角形的个数为2；
（1）当
时，请在图3中画出使三角形个数最少的图形，此时图中三角形的个数是多少？
（2）试猜想当对点时，按上述规则画出的图形中，最少有多少个三角形？（3分）
（3）当
时，按上述规则画出的图形中，最少有多少个三角形？（2分）
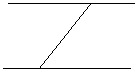
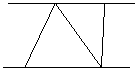
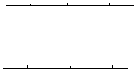
图1 图2 图3
25． （2005年河北省）如图1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．
（1）如图2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；
（2）若三角尺GEF旋转到如图3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．
四、拓广探索（共15分）
26．（2006年安徽北师大）老师在黑板上写出三个算式： 5
一 3= 8×2，9-7=8×4，15-3=8×27，王华接着又写了两个具有同样规律的算式：11
5 =8×12，15-7=8×22，……
(1)请你再写出两个（不同于上面算式）具有上述规律的算式；
(2)用文字写出反映上述算式的规律；
(3 )证明这个规律的正确性．
参考答案：
一、填空题
1．10,3n+1
2．(1)13；(2)3n+l
3．答案不惟一，如∠CBA=∠DBA；∠C=∠D；∠CBE=∠DBE；AC=AD
4．
5．
6．201
7．
8．79
9．
10．等边三角形内任意一点到三边的距离之和等于该等边三角形的高。
二、选择题
11．D 12．C 13．B 14．C 15．C 16．D 17．B 18．B 19．D 20．D
三、解答题
21．（1）16，9（每填对一个给2分）
（2）设第个图形中圆点的个数和五角星的个数相等。
观察图形可知 
解得 
或
（舍去）
所以图形第
个图形中圆点的个数和五角星的个数相等
22．解：（1）1，5，9，13
（奇数）
4，8，12，16
（偶数）
（2）由（1）可知位偶数时
根据题意得
（不合题意舍去）
∴ 存在偶数 
，使得
23．略
24．（1）
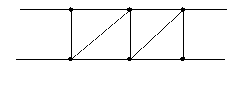4
（2）当有对点时，最少可以画
个三角形
（3）
个
答：当
时，最少可以画4010个三角形。
25．解：⑴①DE=EF；②NE=BF。
③证明：∵四边形ABCD是正方形，N，E分别为AD，AB的中点，
∴DN=EB
∵BF平分∠CBM，AN=AE，∴∠DNE=∠EBF=90°+45°=135°
∵∠NDE+∠DEA=90°，∠BEF+∠DEA=90°，∴∠NDE=∠BEF
∴△DNE≌△EBF
∴ DE=EF，NE=BF
⑵在DA边上截取DN=EB（或截取AN=AE），连结NE，点N就使得NE=BF成立（图略）
此时，DE=EF
26．解：（1）略；（2）规律：任意两个奇数的平方差等于8的倍数；
（3）证明：设m、n为整数，两个奇数可表示为
和
则
当m、n同是奇数或偶数时，m－n一定是偶数，所以
一定是8的倍数；
当m、n一奇一偶时，则
一定是偶数，所以
一定是8的倍数；
所以，任意两奇数的平方差是8的倍数。