中考数学专题复习2：阅读理解题
Ⅰ、综合问题精讲 ：
阅读理解型问题以内容丰富、构思新颖别致、题样多变为特点．知识的覆盖面较大，它可以是阅读课本原文，也可以是设计一个新的数学情境，让学生在阅读的基础上，理解其中的内容、方法和思想，然后在把握本质，理解实质的基础上作出回答．这类问题
的主要题型有：阅读特殊范例，推出一般结论；阅读解题过程，总结解题思路和方法；阅读新知识，研究新问题等．这类试题要求考生能透彻理解课本中的所学内容，善于总结解题规律，并能准确阐述自己的思想和观点，考查学生对数学知识的理解水平、数学方法的运用水平及分析推理能力、数据处理能力、文字概括能力、书面表达能力、随机应变能力和知识的迁移能力等．因此，在平时的学习和复习中应透彻理解所学内容．搞清楚知识的来龙去脉，不仅要学会数学知识，更要掌握在研究知识的过程中体现出的数学思想和方法．
Ⅱ、典型例题剖析
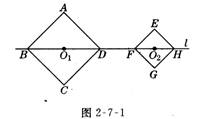【例1】（2005，模拟，9分）如图 2－7－1所示，正方形ABCD和正方形EFGH的边长分别为2和，对角线BD、FH都在直线
上，O1、O2分别是正方形的中心，线段O1O2的长叫做两个正方形的中心距．当中心O在直线 上平移时，正方形 EFH也随之平移，在平移时正方形EFGH的形状、大小没有改变．
（1）计算：O1D=_______，O2 F=______；
（2）当中心O2在直线 l上平移到两个正方形只有一个公共点时，中心距O1 O2 =_________.
（3）随着中心 O2在直线 l上的平移，两个正方形的公共点的个数还有哪些变化？并求出相对应的中心距的值或取值范围．（不必写出计算过程）
解：（1）O1D=2，O2 F=1；（2）O1 O2 =3；
（2）当O1 O2＞3或0≤O1 O2＜1时，两个正方形无公共点；
当O1 O2=1时，两个正方形有无数个公共点；
当1＜O1 O2＜3时，两个正方形有2个公共点．
点拨：本题实际上考查的知识点是“两圆的位置关系”，但形式有所变化．因此，可以再次经历探索两个圆之间的位置关系，认真分析并总结两圆五种位置关系所对应的圆心距d与半径R和r的数量关系，五种位置关系主要由两个因素确定：①公共点的个
数；②一个圆上的点在另一个圆的外部还是内部，按这两个因素为线索来探究位置关系．然后，把这种利用平移实验直观探索方法迁移到研究“两个正方形的位置关系”上来．
【例2】（2005，内江，9分）阅读材料，大数学家高斯在上学读书时曾经研究过这样一个问题：
1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+
，其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…
＝？
观察下面三个特殊的等式：
将这三个等式的两边相加，可以得到1×2+2×3+3×4＝
读完这段材料，请你思考后回答：
⑴ 
；
⑵ 
；
⑶ ；
（只需写出结果，不必写中间的过程）
解：⑴343400(或
)
⑵
⑶
每相邻两个自然数相乘再求和时可以发现结果总是
，但当每相邻三个自然数相乘再求和时就成为了。
【例3】（2005，安徽课改，8分）下面是数学课堂的一个学习片断．阅读后，请回答下面的问题：
学习等腰三角形有关内容后，张老师请同学们交流讨论这样一个问题：“已知等腰三角形ABC的角A等于30°，请你求出其余两角”．同学们经片刻的思考与交流后，李明同学举手讲：“其余两角是30°和120°”；王华同学说：“其余两角是75°和75°”．还有一些同学也提出了不同的看法…．
（1）假如你也在课堂中，你的意见如何？为什么？
（2）通过上面数学问题的讨论，你有什么感受？（用一句话表示）
（1）答：上述两同学回答的均不全面，应该是：其余两角的大小是75°和75°或30°和120°．理由如下：
（i）当
是顶角时，设底角是
．
， 
．
∴其余两角是75°和75°．
（ii）当∠A是底角时，设顶角是β，
， 
．
∴其余两角分别是0°和120°．
（2）（感受中答有：“分类讨论”，“考虑问题要全面”等能体现分类讨论思想的给2分，回答出“积极发言”、“参与讨论”等与数学问题联系不紧密的语句给1分．）
点拨：此题应树立分类讨论思想，考虑问题要全面．
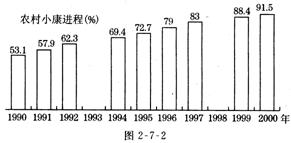
【例4】（2005，贵阳模拟），8分）阅读材料，解答问题：图2－7－2表示我国农村居民的小康生活水平实现程度．地处西部的某贫困县，农村人口约50万，2002年农村小康生活的综合实现程度才达到68％，即没有达到小康程度的人口约为（1－68 ％）×50万= 16万．
（1）假设该县计划在2002年的基础上，到2004年底，使没有达到小康程度的16万农村人口降至 10．24万，那么平均每年降低的百分率是多少？
（2）如果该计划实现，2004年底该县农村小康进程接近图2－7－2中哪一年的水平？（假设该县人口2年内不变）
解：（1）设平均每年降低的百分率为。
据题意，得 16（1－x）2 =10.24，
（1－x）2 =0．64,（1－x）= ±0.8，x1=1.8（不合题意，舍去），x2=0.2．
即平均每年降低的百分率是20％.
（2）×100%=7 9.52％.
所以根据图2－7－2所示，如果该计划实现，2004年底该县农村小康进程接近1996年全国农村小康进程的水平．
点拨：此题属于利用方程解决实际问题，但和原来的实际应用问题的情境不同，需在理解材料的基础上进行．
【例5】（2004，山西）已知p2-p-1=0,1-q-q2=0,且pq≠1，求
的值.
解：由p2-p-1=0及1-q-q2=0,可知p≠0,q≠0
又∵pq≠1,∴
∴1-q-q2=0可变形为
的特征
所以p与
是方程x 2- x -1=0的两个不相等的实数根则
根据阅读材料所提供的方法，完成下面的解答.
已知：2m2-5m-1=0,
,且m≠n
求：
的值.
解：由2m2-5m-1=0知m≠0，∵m≠n，∴
得
根据
的特征
∴
是方程x 2+5 x -2=0的两个不相等的实数根 ∴
Ⅲ、综合巩固练习
（80分 80分钟）
1．（l0分）阅读以下材料并填空：
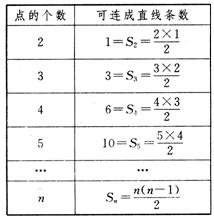平面上有n个点（n≥2）且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线下①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成动条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
②归纳：考察点的个数n和可连成直线的条数SJ发现如下表所示：
③推理：平面上有n个点，两点确定一条直线，取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n（n－1）条直线．但AB与BA是同一条直线，故应除以2，即Sn=
④结论：Sn=
试探究以下问题：
平面上有n个点（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
⑴ 分析：当仅有3个点时，可作_______个三角形；当有4个点时，可作_______个三角形；当有5个点时，可作_______个三角形……
⑵ 归纳：考察点的个数n和可作出的三角形的个数Sn发现：
⑶ 推理：
⑷ 结论：
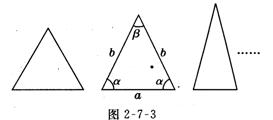
2．（10分）如图2－7－3所示，这些等腰三角形与正三角形的形状有差异，我们把它与正三角形的接近程度称为“正度”，在研究“正度”时，应保证相似三角形的“正度”相等．设等腰三角形的底和腰分别为儿为，底角和顶角分别为以尽要求“正度”的值是非负数．同学甲认为：可用式子
来表示“正度”，的值越小，表示等腰三角形越接近正三角形；同学乙认为：可用式子
来表示“正度”，的值越小，表示等腰三角形越接近正三角形．
探究：
⑴ 他们的方案哪个较为合理，为什么？
⑵ 对你认为不够合理的方案，请加以改进（给出式子即可）
⑶ 请再给出一种衡量“正度”的表达式．
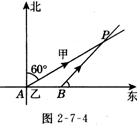
3．（10分）如图2－7－4所示，甲、乙两辆大型货车于下午2：00同时从A地出发驶往P市，甲车沿一条公路向北偏东60o方向行驶，直达P市，其速度为30千米/时；乙车先沿一条公路向正东方向行驶半小时后到达B地，卸下部分货物，再沿一条通向东北方向的公路驶往P市，其速度始终为40千米/时．
⑴ 设出发后经过t小时，甲车与P市的距离为s千米,求s与t之间的函数表达式，并写出自变量t的取值范围．
⑵ 已知在P市新建的移动通讯接收发射塔，其信号覆盖面积只可达P市周围方圆30千米的区域（包括边缘地带人除此之外，该地区无其他发射塔．故甲、乙两车司机只能靠P市发射塔进行手机通话联系，问甲、乙两车司机从什么时刻开始可取得联系（精确到分钟）
4、（10分）阅读下面材料：在计算3+5+ 7+ 9 + 11+13 +15+17+19+21时，我们发现，从第一个数开始，以后 的每个数与它的前一个数的差都是一个相同的定值，具有这种规律的一列数，除了直接相加外，我们还可以用公式
来计算它们的和（公式中的n表示数的个数，a表示第一个数的值，d表示这个差的定值）,那么3+5+ 7+ 9 + 11+13 +15+17+19+21=
×2=120.
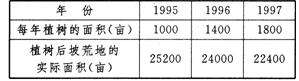
用上面的知识解决下列问题：为了保护长江，减少水土流失，我市某县决定对原有的坡荒地进行退耕还林，从1995年起在坡荒地上植树造林，以后每年又比上一年多植相同面积的树木改造坡荒地，由于每年因自然灾害，树木成活率，人为因素等的影响，都有相当数量的新坡荒地产生，下表为1995、1996、1997三年的坡荒地面积和植树的面积的统计数据，假设坡荒地全部种上树后，不再水土流失形成新的坡荒地．问到哪一年，可以将全县的所有坡荒地全部种上树木？
8．(10分)如果两个三角形不仅是相似三角形，而且每组对应点所在的直线都经过同一个点，那么这两个三角形叫作位似三角形．它们的相似比又称为位似比，这个点叫做位似中心．利用三角形的位似可以将一个三角形缩小或放大．
⑴ 选择；如图2－7－5⑴所示，点O是等边三角形PQR的中心，P′、Q′、R′分别是OP、OQ、OR的中点．则△P′Q′R′与△PQR是位似三角形．此时，△P′Q′R′与△PQR的位似比、位似中心分别为（ ）
A．2，点P B．，点P C．2，点O D．，点O
⑵ 如图2－7－5⑵所示，用下面的方法可以画面AOB的内接等边三角形．阅读后证明相应问题：
画法：①在△AOB内画等边三角形CDE，使点C在OA上，点D在OB上； ②连接OE并延长，交AB于点E′，过点E′作E′C′∥EC，交OA于点C′，作E′D′∥ED，交OB于点D′；
③连接C′D′，则ΔC′D′E′是△AOB的内接三角形， 求证：△C′D′E′是等边三角形．
