中考数学总复习专题训练（八)
（三角形）
考试时间：120分钟 满分150分
一、选择题（每小题3分，共45分）
1.若等腰三角形底角为72°，则顶角为（ ）。
A．108° B．72° C．54° D．36°
2.三角形的两边长分别为3和6，第三边的长是方程x2－6x＋8＝0的一个根，
则这个三角形的周长是（ ）。
A．9 B．11 C．13 D．11或13
3. 下列条件能确定△ABC是直角三角形的条件有（ ）。
(1) ∠A+∠B=∠C； (2) ∠A:∠B:∠C=1:2:3；
(3) ∠A=90°-∠B；
(4)∠A=∠B=
∠C
A．1个 B．2个 C．3个 D．4个
4.以下列各组数为边长，能组成直角三角形的是（ ）。
A.8，15，17 B.4，5，6 C.5，8，10 D.8，39，40
5.等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（ ）。
A．60° B．120° C．60°或150° D．60°或120°
6.已知ΔABC的三边分别是
,则ΔABC的面积是（ ）
。
A．6 B．7.5 C．10 D． 12
7. 下面给出的几种三角形：（1）有两个角为60°的三角形；(2)三个外角都相等的三角形；(3)一边上的高也是这边上的中线的等腰三角形；(4)有一个角为60°的等腰三角形。其中一定是等边三角形的有（ ）。
A．4个 B．3个 C．2个 D．1个
8.已知△ABC，
⑴如图1，若P点是∠ABC和∠ACB的角平分线的交点，则∠P=90°
∠A；
⑵如图2，若P点是∠ABC和外角∠ACE角平分线的交点，则∠P=90°－∠A；
⑶如图3，若P点是外角∠CBF和∠BCE角平分线交点，则∠P=90°－∠A。
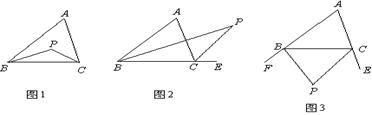
上述说法下确的个数是（ ）。
A．0个 B．1个 C．2个 D．3个
9.如图4，工人师傅砌门时，常用木条EF固定矩形门框ABCD，使其不变形，这种做法的根据是（ ）。
A.两点之间线段最短 B.矩形的对称性
C.矩形的四个角都是直角 D.三角形的稳定性
10.如图5，在菱形ABCD中，E、F分别是AB、CD的中点，如果EF =2，那么菱形ABCD的周长是（ ）。
A．4 B．8 C．12 D．16
11.如图6，平行四边形ABCD中，对角线AC和BD相交于点O，如果AC=12 , BD=10, AB=m ，那么m的取值范围是（ ）。
A.10<m<12 B.2<m<22 C.1<m<11 D.5<m<6
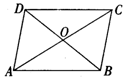
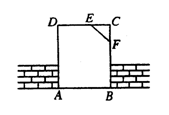
图4 图5 图6
12.下图能说明∠1＞∠2的是（ ）。
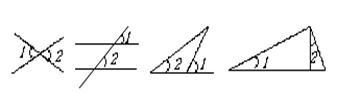
A B C D
13.若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC为公共边的“共边三角形”有（ ）。
A．2对 B．3对 C．4对 D．6对
14.如图7，△ABC、△ADE及△EFG都是等边三角形，D和G分别为AC和AE
的中点.若AB＝4时，则图形ABCDEFG外围的周长是（ ）。
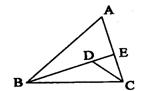A．12 B．15 C．18 D．21
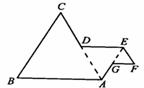
图7 图 8
15.一个等腰三角形底边上的高是4，周长是16，则三角形的面积是（ ）。
A．24 B．12 C．10 D．8
二、填空题（每小题3分，共36分）
1. 在△ABC中，若∠A：∠B：∠C=2：3：4，则∠C=_________。
2. 若一个三角形的两个内角分别为50°、80°，则这个三角形是_________三角形。
3. 三角形的三边长为3,a,7,则a的取值范围是________________。
4.如图9，在△ABC中，∠ABC=90°，∠A=50°，BD∥AC，则∠CBD的度数是_________。
5. 如图10， 已知△ABC中，AB＝AC，∠BAC与∠ACB的平分线交于D点，∠ADC＝130°，那么∠CAB的大小是_________。
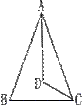
图9 图10
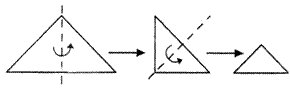
6.如图所示，把腰长为
的等腰直角三角形折叠两次后，得到的一个小三角形的周长是_________。
 |
7. 如图11，△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC，DE∥BC，则图形中共有_________个等腰三角形。
8.如图12，在△ABC中，AB＝12，AC＝5，∠BAC＝90º。若点P是BC的中点，则线段AP的长等于_________；若点P在直线BC上运动，设点B，C关于直线AP的对称点分别为B′C′，则线段B′C′的长等于_________。
9.如图13，在△ABC中，AB=AC，∠BAD=20°，且AE=AD，则∠CDE＝_________。
 |
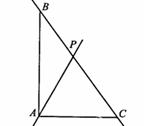
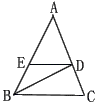
图11 图12 图13
10.在方格纸上，每个小格的顶点叫格点，以格点为顶点的三角形叫格点三角形. 如图14，在4×4的方格纸上，以AB为边的格点三角形ABC的面积为2个平方单位，则符合条件的C点共有_________个。
11. 如图15是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是a，则六边形的周长是_________。
12．如图16，P是正三角形 ABC 内的一点，且PA＝6，PB＝8，PC＝10．若将△PAC绕点A逆时针旋转后，得到△P'AB ，则点P与点P' 之间的距离为_________，∠APB＝_________。
 |
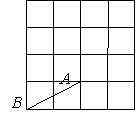
图14 图15 图16
三、解答下列各题（第1题9分，其余每小题10分，共69 分）
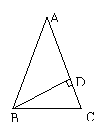1. 如图，已知△ABC中，∠ABC=∠ACB=2∠A，且BD⊥AC，垂足为D，求∠DBC的度数。
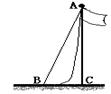2.如图,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直, 则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
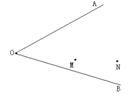
3.如图，在∠AOB内，求作点P，使P点到OA、OB的 距离相等，并且P点到M、N的距离也相等。（保留作图的痕迹，写出作法）。
4.已知：如图，
∥
，
是
的中点，求证：是
中点。
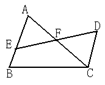
5.已知：如图，AB=AD， CB=CD，E，F分别是AB，AD的中点.求证：CE=CF 。
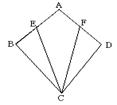
6.如图，△ABC中，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F。求证：
（1）AD⊥EF ；
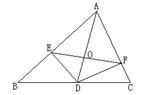（2）当有一点G从点D向A运动时，DE⊥AB于E，DF⊥AC于F，此时上面结论是否成立？
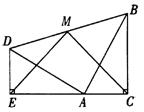7.两个全等的含300, 600角的三角板ADE和三角板ABC如图所示放置，E,A,C三点在一条直线上，连结BD，取BD的中点M，连结ME，MC．试判断△EMC的形状，并说明理由．
参考答案
一、1、D 2、C 3、D 4、A 5、D 6、A 7、B 8、C 9、D 10、D 11、C 12、C 13、B 14、B 15、B
二、1、80°； 2、等腰； 3、4＜a＜10； 4、40°；5、10°；6、
； 7、5； 8、
，13；9、10°； 10、4；11、30a ；12、6 ，150°。
三、1、18°；2、设旗杆的高度为x米
列方程 
，解得 
。3、分别作∠AOB的平分线和MN的垂直平分线交点就是P点。
4、证△FAE≌△FCD。
5、连结AC 先证△ABC≌△ADC 再证△AEC≌△DFC 。
6、先证△AED≌△AFD 得AE=AF ∠EAD=∠FAD 由等腰三角形三线合一得 AD⊥EF。（或 证AE=AF DE=DF 得A点在EF的中垂线上，D点在EF的中垂线上 ）
7、△EMC是等腰直角三角形。
证明：由题意，得
DE=AC，∠DAE＋∠BAC900.
∠DAB=900。连接AM．∵DM=MB
∴MA=
DB=DM,∠MDA=∠MAB=450.
∴∠MDE=∠MAC=1050
∴△EDM≌△CAM
∴EM=MC, ∠DME=∠AMC。
又∠EMC=∠EMA+∠AMC=∠EMA+∠DME=900
∴CM⊥EM，所以△EMC是等腰直角三角形。