中考数学总复习专题训练（九)
（四边形）
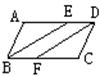
考试时间：120分钟 满分150分
一、选择题（每小题3分，共30分）
1．如图1，在□ABCD中，对角线AC、BD交于点O，下列式子中 一定成立的是( )。
A．AC⊥BD B．OA=0C
C．AC=BD D．A0=OD
2．如图2，等腰梯形ABCD中，AD∥BC，若将腰AB沿A→D的方
向平移到DE的位置，则图中与∠C相等的角（不包括∠C）有（ ）。
A．1个 B．2个 C．3个 D．4个
3．将一矩形纸片按如图3方式折叠，BC、BD为折痕，折叠后
与在同一条直线上，则∠CBD的度数为（ ）。
A． 大于90° B．等于90°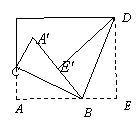 
C．小于90° D．不能确定
 |
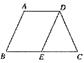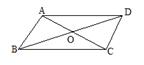
图1 图2 图3
4．如图4，梯形ABCD中，对角线AC与BD交于点O，则图中面积相等的三角形有（ ）。
A．3对 B．2对 C．1对 D． 4对
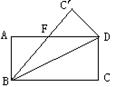
5．如图5，将矩形ABCD沿对角线BD对折，使点C落在C′处，BC′交AD于F，下列不成立的是（ ）。
A．AF＝C′F B．BF＝DF
C．∠BDA＝∠ADC′ D．∠ABC′＝∠ADC′
6．如图6，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，E为垂足，连接DF．则∠CDF等于（ ）。
Ａ．80° B．70° C．65° D．60°
 | |||||
 | |||||
 | |||||
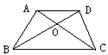图4 图5 图6
7．在□ABCD中，∠A比∠B大30°，则∠C的度数为（ ）。
A．120° B．105° C．100° D．75°
8．如图7，在菱形ABCD中，
，则菱形AB边上的高CE的长是（ ）。
A．
B．
C． ５ D．１０
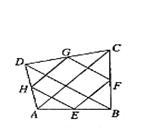
9.如图8，任意四边形ABCD各边中点分别是E、F、G、H，若对角线AC、BD的长都为20cm，则四边形EFGH的周长是（ ）。
A．80cm B．40cm C．20cm D．10cm
 |
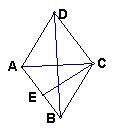图7 图8
10．在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成三角形，又能拼成平行四边形和梯形的可能是（ ）。
二、填空题（每小题3分，共30分）
1．如图9，平行四边形ABCD中，E，F分别为AD，BC边上的一点．若再增加一个条件＿＿＿＿＿＿＿＿＿，就可得BE=DF。
2．将一矩形纸条，按如图10所示折叠，则∠1 = _______度。
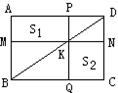
3．如图11，矩形ABCD中，MN∥AD，PQ∥AB，则S1与S2的大小关系是______。
 |  | ||||
 | |||||
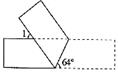图9 图10 图11
4．已知平行四边形ABCD的面积为4，O为两对角线的交点，则△AOB的面积是 。
5．菱形的一条对角线长为6cm，面积为6cm2，则菱形另一条对角线长为______cm。
6．如果梯形的面积为216cm2，且两底长的比为4:5，高为16cm，那么两底长分别为__________。
7．如图12，在菱形ABCD中，已知AB＝10,AC＝16,那么菱形ABCD的面积为 。
8．如图13，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠EFB＝65°，则∠AED′＝______。
9．如图14，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的度数等于______。
 |
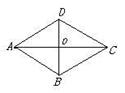
图12 图13 图14
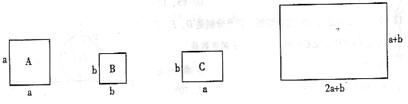
10．有若干张如图所示的正方形和长方形卡片，如果要拼一个长为（2a + b），宽为（a + b）的矩形，则需要A类卡片 张，B类卡片 张，C类卡片 张。
三、解答下列各题（第1题12分，其余每小题13分，共90分）
1．如图，已知平行四边形ABCD，AE平分∠DAB交DC于E，BF平分∠ABC交DC于F，DC=6cm，AD=2cm，求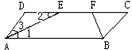
DE、EF、FC的长．
2．如图，已知矩形ABCD中，AC与BD相交于O，DE平分∠ADC交BC于E，∠BDE＝15°，试求∠COE的度数。
 |
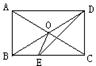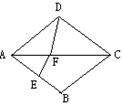
3．如图，在正方形ABCD中，Q是CD的中点，P在BC上，且AP=PC+CD，
求证：AQ平分∠DAP。
 |
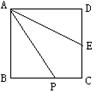4．如图甲，四边形ABCD是等腰梯形，AB∥DC，由4个这样的等腰梯形可以拼出图乙所示的平行四边形．
（1）求梯形ABCD四个内角的度数；
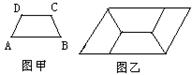（2）试探究四边形ABCD四条边之间
存在的等量关系，并说明理由；
5．如图，菱形公园内有四个景点，请你用两种不同的方法，按要求设计成四个部分：
（1）用直线分割；
（2）每个部分内各有一个景点；
（3）各部分的面积相等．
（只要求画图正确，不写画法）
 |
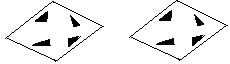6．一组线段AB和CD把正方形分成形状相同，面积相等的四部分，现给出四种方法，如图所示，请你从中找出线段AB，CD的位置关系及存在的规律，符合这种规律的线段共有多少组？
 |
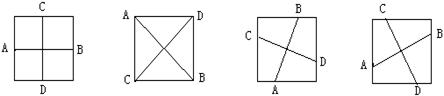7．阅读材料：如图（1），在四边形ABCD中，对角线AC⊥BD，垂足为P，求证：S四边形ABCD=
AC·BD．
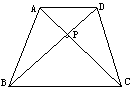
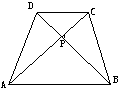
图（1） 图（2）
证明：∵AC⊥BD，∴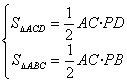
∴S四边形ABCD=S△ACD+
S△ABC=AC·PD+AC·PB=AC（PD+PB）=AC·BD。
解答问题：
（1）上述证明得到的性质可叙述为： ．
（2）已知：如图（2），等腰梯形ABCD中，AD∥BC，对角线AC⊥BD且相交于点P，AD=3cm，BC=7cm，利用上述的性质求梯形的面积。
参考答案
一、 1、B； 2、C； 3、B； 4、A； 5、C； 6、D；7、B； 8、A； 9、B；10、C。
二、1、答案不唯一，如AE=CF或BE∥DF等； 2、52； 3、S1＝S2； 4、1； 5、2； 6、12 cm和15cm； 7、96 ； 8、50°； 9、30； 10、2，1，3．
三、1、因为四边形ABCD是平行四边形，所以AB//CD，
AD=BC（平行四边形的对边平行且相等），所以∠1=∠2（两直线平行，内错角相等），又因为AE平分∠DAB，所以∠1=∠3，所以∠2=∠3，所以DA=DE=2cm（等角对等边）．同理BC=CF=2cm．所以EF=DC—DE—CF=6 cm —2 cm —2 cm =2 cm．
2、由“四边形ABCD是矩形，DE平分∠ADC”知∠CDE＝∠CED＝45°，又∠BDE＝15°，所以∠CDO＝60°，由矩形的特征“对角线互相平分”可知， OD＝OC，故△OCD是等边三角形，从而有OC＝OD＝CE，∠DCO＝60°，∠OCB＝30°，进而求得∠COE＝75°．
3、如图，延长AQ交BC的延长线于E．因为四边
形ABCD是正方形，所以AD=CD，AD∥BE．又Q是CD的
中点．因此，△ADQ与△ECQ关于点Q成中心对称．则有
AD＝CE，∠1＝∠E．又因为AP＝PC＋CD，所以AP＝PC＋
CE，于是∠2＝∠E． 故∠1＝∠2，即有AQ平分∠DAP．
4、（1）只要善于观察就不难看出底角的三倍等于180°或三个顶角拼成了一个周角，即∠A＝∠B＝60°，∠C＝∠D＝120°；
（2）AB＝2BC＝2CD＝2AD．
5、答案不唯一，有许多种画法，如：
 |
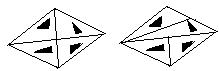6、AB⊥CD且AB与CD均过正方形的中心，符合这种规律的线段有无数组。
7、（1）对角线互相垂直的四边形的面积等于对角线乘积的一半．
（2）由已知，易得AC=BD=5
cm，利用上述性质，得S梯形=AC·BD=25cm2