中考数学总复习专题训练（七)
（角、相交线与平行线）
考试时间：120分钟 满分150分
一、选择题（每小题4分，共40分）
1．下列说法中，正确的有（ ）。
（1）过两点有且只有一条线段（2）连结两点的线段叫做两点的距离
（3）两点之间，线段最短 （4）AB＝BC，则点B是线段AC的中点
(5) 射线比直线短
A．1个 B．2个 C．3个 D．4个
2．现在的时间是9点20分，此时钟面上的时针与分针的夹角是（ ）。
A．
B．
C．
D．
3．两平行直线被第三条直线所截，同位角的平分线（ ）。
A．互相重合 B．互相平行 C．互相垂直 D．相交
4．如果∠1与∠2互补，∠1与∠3互余，那么（ ）。
A．∠2＞∠3 B．∠2=∠3
C．∠2＜∠3 D．∠2≥∠3
5．如图1，已知∠1=∠B，∠2=∠C，则下列结论不成立的是（ ）。
A．AD∥BC B．∠B=∠C C．∠2+∠B=180° D．AB∥CD
6．如图2，直线AB、CD相交于点O，EF⊥AB于O，且∠COE=50°，则∠BOD等于（ ）。
A．40° B．45° C．55° D．65°
7．如图3，若AB∥CD，则∠A、∠E、∠D之间的关系是（ ）。
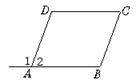
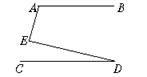
图1 图2 图3
A．∠A+∠E+∠D=180° B．∠A－∠E+∠D=180°
C．∠A+∠E－∠D=180° D．∠A+∠E+∠D=270°
8．如图4所示，
∥
，∠1=120°，∠2=100°，则∠3=（
）。
A．20° B．40° C．50° D．60°
9．如图5，AB∥CD ，直线EF分别交AB，CD于E，F两点，∠BEF的平
分线交CD于点G，若∠EFG＝72°，则∠EGF等于（ ）。
A． 36° B． 54° C． 72 ° D． 108°
10．把一张长方形的纸片按如图6所示的方式折叠，EM、FM为折痕，折叠后的C点落在
或的延长线上，则∠EMF的度数是（ ）。
A．85° B．90° C．95° D．100°
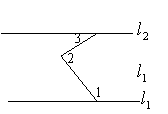
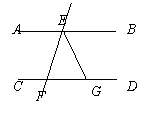
图4 图5 图6
二、填空题（每小题4分，共40分）
1．如图1，直线AB、CD相交于点O，OB平分∠DOE，若∠DOE=60°则∠AOC的度数是_________。
2．如图2，若l1∥l2，∠1=45°，则∠2=_________。
3．如图3，已知直线a∥b，c∥d，∠1=115°，那么∠2=_________，
∠3=_________。
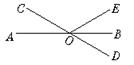
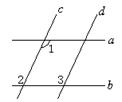
图1 图2 图3
4．如图4，已知直线AB、CD、EF相交于点O，∠1=95°，∠2=32°，则∠BOE=_________。
5．如图5，∠1=82°，∠2=98°，∠3=80°,则∠4的度数为_________。
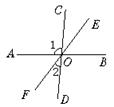
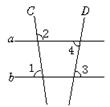
图4 图5
6．如图6，AD∥BC，AC与BD相交于O，则图中相等的角有_________对。
7．如图7，已知AB∥CD，∠1=100°，∠2=120°，则∠α=_________。
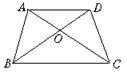
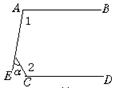
图6 图7
8．如图8，DAE是一条直线，DE∥BC，则∠BAC=_________。
9．如图9，AB∥CD，AD∥BC，则图中与∠A相等的角有_________个。
10．如图10，标有角号的7个角中共有_________对内错角，_________对同位角，_________对同旁内角。
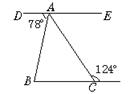
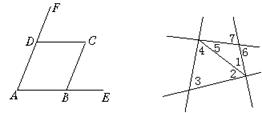
图8 图9 图10
三、解答下列各题（第1题7分，其余每小题9分，共70分）
1．如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数。
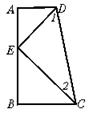
2．如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求
∠DCN的度数。
3．已知：如图，CB⊥AB，CE平分∠BCD，DE平分∠CDA,并且
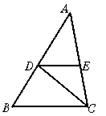
∠1+∠2=90°，求证：DA⊥AB。
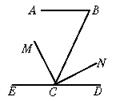
4．如图，BC∥DE，小颖用量角器分别画出∠ABC、∠ADE的角平分线BG、DH，想一想，小颖所画的这两条射线BG和DH会平行吗？为什么？
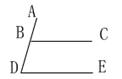
5．如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=75°，求∠BFD度数。
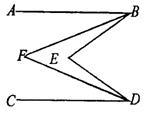
6．如图, AB//CD, 若∠ABE=1200, ∠DCE=350, 求∠BEC度数。
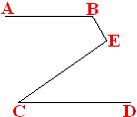
7.如图，已知AB∥CD ∠DAB＝∠DCB,AE平分∠DAB 且交DC于E,CF平分
∠DCB且交AB于F。求证: AE∥FC。
 |
8．如图，线段AB上的点数与线段的总数有如下关系：如果线段上有3个点时，线段共有3条；如果上有4个点时，线段共有6条；如果线段上有5个点时，线段共有10条；⑴当线段上有6个点时，线段共有多少条？⑵当线段上有n个点时，线段共有多少条？（用n的代数式表示）⑶当n=100时，线段共有多少条？
参考答案
一、1、A 2、B 3、B 4、A 5、B 6、A 7、C 8、B
9、B 10、B
二、
1.30°
2.135
3.115° 115°
4. 53°
5.80°
6.四
7.40°
8.46°
9.3
10.四 二 四。
三、
1、40°；
2、32.5°；
3、提示：证明AD//BC；
4、BG//DH。理由是：∵BC∥DE，∴∠ABC＝∠ADE，∴∠ABG＝∠ADH，∴BG//DH。
5、37.5°；
6、95°；
7、先证AD∥BC，再证∠AEB＝∠FCB。
8、15，
，4950。