中考数学总复习专题训练（三)粤教

中考数学总复习专题训练（三)　

 （方程与不等式）

考试时间：120分钟 满分150分

一、选择题（每小题3分，共45分）

1．方程x² = x +1的根是（　 ）。

Ａ．x = 　Ｂ． x = Ｃ． x =±  Ｄ． x =

2．，则不等式的解集是（　 ）。

Ａ．　　 Ｂ．　　　 Ｃ．　　　Ｄ．

3．如果不等式组的解集是，那么的值是（　 ）。

Ａ．　　　　 Ｂ．　　　　Ｃ．　　 Ｄ．

4．不等式2x－1≥3x-5的正整数解的个数为（　 ）。

Ａ．1个　　 Ｂ．2个　　　 Ｃ．3个　　　Ｄ．4个

5．若关于x的方程2x－4=3m和x+2=m有相同的根，则m的值是（　 ）。

Ａ． 10　　　Ｂ．－8　　　Ｃ．－10　　 Ｄ． 8

6．代数式 与代数式 k +3 的值相等时，k 的值为（　 ）。

 Ａ． 7　　　 Ｂ． 8　　　　Ｃ． 9　　 　　Ｄ． 10

7．若 m + 1与 互为相反数，则m的值为（　 ）。

　 Ａ． 　　　Ｂ．- 　　　　Ｃ．- 　　　 Ｄ．　

8．由方程组可得出与的关系是（　 ）。

　　Ａ．　　Ｂ．　Ｃ．　 Ｄ．

9．若方程组的解为x、y，且2<k<4，则x-y的取值范围是（　 ）。

Ａ．0<x-y<　　Ｂ．0<x-y<1　　Ｃ．-3<x-y<-1　　Ｄ．-1<x-y<1

10．如果中的解x、y相同，则m的值是（　 ）。

Ａ．1　　　　 Ｂ．－１　　 Ｃ．2　　　　 Ｄ．－2

11．足球比赛的记分为：胜一场得3分，平一场得1分，负一场得0分，一队打了14场比赛，负5场，共得19分，那么这个队胜了（　 ）。

Ａ．3场　　　Ｂ．4场　　　Ｃ．5场　　　Ｄ．6场

12. 当分母解x 的方程＝时产生增根，则m的值等于（　 ）。

　　Ａ．－2　　　Ｂ．－1　　　Ｃ．1.　　　　Ｄ．2

13.一种药品经两次降价，由每盒50元调至40.5元，平均每次降价的百分率是　　（　 ）。

Ａ．5％　　　　 Ｂ． 10％　　 Ｃ．15％　 　　 Ｄ． 20％

14．如图，宽为的矩形图案由个全等的小长方形拼成，其中一个小长方形的面积为（　 ）。

Ａ．　　　　Ｂ．　　

Ｃ．　　Ｄ．

15．年前，母亲的年龄是儿子的倍；年后，母亲的年龄是儿子的 倍．求母子现在的年龄．设母亲现年岁，儿子现年岁，列出的二元一次方程组是（　 ）。

　　Ａ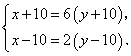．　　 Ｂ．

　　Ｃ．　　　Ｄ．

二、填空题（每小题3分，共45分）

1．已知方程4x+5y=8，用含x的代数式表示y为__________________。

2．方程x+2y=5在正整数范围内的解是____________________。

3.已知方程3x²－19x+m=0的一个根是1，那么它的另一个根是_________，m=_________。

4.若方程x²+mx－1=0的两个实数根互为相反数，那么m的值是_________。

5.当m=　　 时，方程x²+mx+4=0有两个相等的实数根； 当m=　　 时，方程mx²+4x+1=0有两个不相等的实数根；

6. 方程2x(mx－4)=x²－6没有实数根，则最小的整数m=_________。

7. 一元二次方程x²+px+q=0两个根分别是2+和2－，则p=_________，q=_________。

8．已知方程3x+y=12有很多解，请你写出互为相反数的一组解_________。

9.若2x²－3xy－20y²=0，且 y≠0， 则= _________。

10. 写出一个以为解的一个二元一次方程组_________。

11. 如果x²－2(m+1)x+m²+5是一个完全平方式，则m=_________。

12.若方程x²+(a²－2)x－3=0的两根是1和－3，则a=_________。

13.若关于x的方程x²+2(m－1)x+4m²=0有两个实数根，且这两个根互为倒数，那么m的值为_________。

14.如果关于x的方程x²－4x+m=0与x²－x－2m=0有一个根相同，则m的值为_________。

15.已知方程2x²－3x+k=0的两根之差为2，则k=_________。

三、解答下列各题（ 第8题11分，其余每小题7分，共 60 分）

1.已知a,b,c是三角形的三边长，且方程(a²+b²+c²)x²+2(a+b+c)x+3=0有两个相等的实数根，求证：这个三角形是正三角形

2．已知方程组和方程组的解相同，求的值．

3．车间里有名工人，每人每天能隆产螺母个或螺栓个，若一个螺栓配两个螺母，那么应分配多少人生产螺栓，多少人生产螺母才能使螺栓和螺母正好配套？

4．用图象法解方程组　　　　　　　　　 

5．已知关于x的方程的一个解与方程的解相同。

⑴求k的值；

⑵求方程的另一个解.

6．某商场将进货价为30元的台灯以40元售出，平均每月能售出600个．调查表明：这种台灯的售价每上涨1元，其销售量就将减少10个．为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少？这时应进台灯多少个？

请你利用方程解决这一问题．

7．甲、乙两地间铁路长2400千米, 经技术改造后, 列车实现了提速. 提速后比提速前速度增加20千米/时, 列车从甲地到乙地行驶时间减少4小时. 已知列车在现有条件下安全行驶的速度不超过140千米/时. 请你用学过的数学知识说明这条铁路在现有条件下是否还可以再次提速?

8．某工厂现有甲种原料，乙种原料，计划用这两种原料生产，两种产品共件．已知生产一件种产品，需要甲种原料，乙种原料；生产一件种产品，需要甲种原料，乙种原料，按要求安排，两种产品的生产件数，有哪几种方案？你能设计出来吗？

参考答案

一、1、B　 2、A　 3、D　　4、D　　5、B　 6、B 　7、D　 8、C　 9、B　10、B　11、C　12、A　13、B　14、A　 15、B

二、1、；　2、，； 3、，16；　4、0；5、±4，m＜4且m≠0；　6、2；　7、－4；　　8、；9、或4；10、x+y=-1(不唯一)；11、2；12、±2；13、；14、0或3；15、-2。

三、1．由⊿=0得，所以。

2．通过解方程组求得代入方程组求得a=1,b=-1。

3．设应分配人生产螺栓，人生产螺母，则解得

4．由2x+y=4，得y= －2x+4。由4x+3y=6，得y=。　

在同一坐标系内作出一次函数y= －2x+4的图象和y=的图象，如图(1)，观察图象的交点坐标为（3，－2），∴方程组的解是。

5.（1）∵，　 ∴，　∴。　　　　 

经检验是原方程的解。　

把代入方程中，解得k=－1　。　　

（2）解，得，x₂=－1 。　　

∴方程的另一个解为x=－1 。　

6．设售价为x元，则（x-30）[600-（x-40）×10]=10000，

解得x=50，x=80，即售价为50元时进500个；售价为80元时进200个。

7．设提速后列车速度为x千米/时, 则:

　

解之得: x₁=120　x₂=－100(舍去)

经检验x=120是原方程的根

∵120<140　 ∴仍可再提速

答: 这条铁路在现有条件下仍可再次提速。

8．设生产种产品件，则生产种产品件．根据提意，得解得）。有三种方案：（1）生产种产品件，种产品件；（2）生产种产品件，种产品件；（3）生产种产品件，种产品件。