中考数学总复习专题训练（十)粤教

中考数学总复习专题训练（十)　

（相似形）

考试时间：120分钟 满分150分

一、选择题（每小题4分，共40分）

1．如图1，在△ABC中，AB=AC，∠A=36º，BD平分∠ABC，DE∥BC，那么在

下列三角形中，与△EBD相似的三角形是（　 ）。

A．△ABC　　　 B．△DAB　　  C．△ADE　 　　　D．△BDC

2．如图2，AB∥CD∥EF，则图中相似三角形的对数为（　 ）。

A．1对　　　　　B．2对　　　　 C．3对　　　　　D．4对

3．如图3，已知在△ABC，P为AB上一点，连结CP，以下各条件中不能判定△ACP∽△ABC的是（　 ）。

A．∠ACP＝∠B　　B．∠APC＝∠ACB　 C． ＝　　　D． ＝　

　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　 

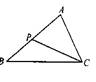
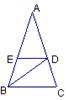
　　　　 图1　　　　　　　　　  图2　　　　　　　　　 图3

4．如图4，在正方形网格上，若使△ABC∽△PBD，则点P应在（　 ）。

A．P₁处　　　　　 B．P₂处　　　　 C．P₃处　　　　 D．P₄处

5．如图5，若A、B、C、D、E、F、G、H、O都是5×7方格纸中的格点，为使△DME∽△ABC，则点M应是F、G、H、O四点中的（　 ）。

A．F　　　　　　  B．G　　　　　  C．H　　　　　　 D．O

6．如图6，梯形ABCD的对角线AC、BD交于点O，若S_ΔAOD：S_ΔACD=1：4，则S_ΔAOD：S_ΔBOC的值为（　 ）。

A．1：3　　　　　 B．1：4　　　　 C．1：9　　　　　D．1：16

 

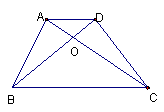
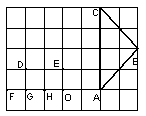
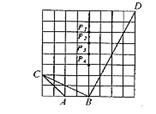
　　　　 图4　　　　　　　　　　 图5　　　　　　　　  图6

7．在等腰△ABC和等腰△DEF中，∠A与∠D是顶角，下列判断正确的是（　 ）。

①∠A=∠D时，两三角形相似；　　　 ②∠A=∠E时，两三角形相似；

③时，两三角形相似；　　　④∠B=∠E时，两三角形相似。

A．1个　　　　  B．2个　　　　  C．3个　　　　　 D．4个

8．在RtΔABC中，∠ACB=90°，CD⊥AB于D，则AC∶BC=2∶3，则AD∶BD=（　 ）。

A．2∶3　　　　 B．4∶9　　　　  C．∶　　 D．不能确定

9．如图7，P是RtΔABC的斜边BC上异于B、C的一点，过点P作直线截ΔABC，使截得的三角形与ΔABC相似，满足这样条件的直线共有（　 ）。

A．1条　　　　 B．2条　　　 C．3条　　　D．4条

10．如图8，路灯距地面8米，身高1.6米的小明从距离灯的底部（点O）20米的点A处，沿OA所在的直线行走14米到点B时，人影长度（　 ）。

A．变短3.5米　 B．变长1.5米  C．变长3.5米　D．变短1.5米

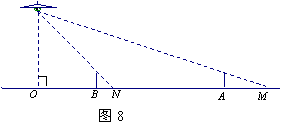
　　　　  图7

二、填空题（每小题4分，共24分）

1．地图上某地的面积为100cm²，比例尺是1∶500，则某地的实际面积是_________m²。

2．在Rt△ABC中，AD为斜边上的高，，则AB∶BC＝_________。

3．如图9，DE∥BC，AD∶DB= 2 ∶3 ，则ΔADE 与ΔABC 的周长之比为_________；面积之比为_________。　　　　　　

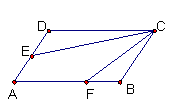
4．如图10，在平行四边形ABCD中，AB=8cm，AD=4cm，E为AD的中点，在AB上取一点F，使△CBF∽△CDE，则AF=_________cm。

5.如图11，一油桶高0.8 m，桶内有油，一根木棒长1m，从桶盖小口斜插入桶内，一端到桶底，另一端到小口，抽出木棒，量得棒上浸油部分长0.8m，则桶内油的高度为_________。

　　　　　　　　　　　　　　　　　　 

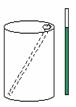
图9　　　　　　　　 图10　　　 　　　　　　 图11

6．在△ABC中，AB＝12，AC＝15，D为AB上一点，BD＝AB，在AC上取一点E，得△ADE，当AE的长为_________时，图中的两个三角形相似。

三、解答下列各题（第8题16分，其余每小题 10分，共86分）

1．如图，在中，EF//DC，DE//BC，求证：AF：FD=AD：DB。

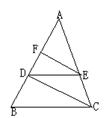
2．如图,菱形ABCD中,CF⊥AD,垂足为E,交BD的延长线于F。求证:

AO²=BO•OF。

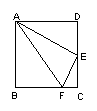
3．如图,正方形ABCD中,E是CD的中点,EF⊥AE。求证:(1)EF平分∠AFC；(2)BF=3FC。

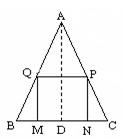
4.如图，正方形MNPQ的顶点在三角形ABC的边上，当边BC=a与高AD=h

满足什么条件时，正方形MNPQ的面积是三角形ABC面积的一半？

5．某社区拟筹资金2000元，计划在一块上、下底分别是10米、20米的梯

形空地上种植花木（如图所示），他们想在地带种植单

价为10元/米²的太阳花，当地带种满花后，已经花了500元，

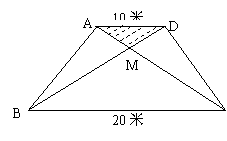请你预算一下，若继续在地带种植同样的太阳花，资金是否够用？

并说明理由。

	C

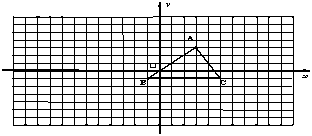
6．如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间

连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形。在建立平面直角坐标系后，点B的坐标为。（1）把△ABC向左平移8格后得到△，画出△的图形并写出点的坐标；(2)把△ABC绕点C按顺时针方向旋转90°后得到△，画出△的图形并写出点的坐标；(3)把△ABC以点A为位似中心放大，使放大前后对应边长的比为1：2，画出△。

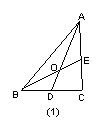
7．在ΔABC中,D为BC的中点,E为AC上的任意一点,BE交AD于点O．某学生在研究这一问题时,发现了如下事实: 如图(1),当时,有；

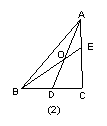
如图(2),当时,有；

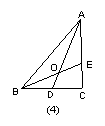
如图(3),当时,有；在图(4)中,当时,

参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明．

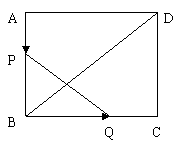8．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点。若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？

参考答案

一、1、B　　2、C　 3、D　　4、C　　5、C　　6、C　　7、C　　8、B　

9、C　 10、A　

二、1、2500米²；2、1∶2；　3、2∶5，4∶25 ；4、7；　5、 0.64m；6、10或。

三、1、提示：证AF：FD=AE：EC =AD：DB ；

2、先证CO=AO,∠FCB=∠FED=90⁰,

又CO⊥BF,

∴CO²=BO·OF． 

3`、(1)延长FE,AD交于G．

先证ΔDEG≌ΔCEF,得∠G=∠EFC,

而∠G=∠GFA．

(2)先证ΔADE∽ΔECF,

得CF∶CE=DE∶DA=1∶2,

∵CE=ED,CD=CB,

从而CF∶CD=CF∶CB=1∶4．

∴BF=3CF．

4、

5、梯形ABCD中AD//BC∽，　

AD=10，BC=20　　　　

 ∵，

还需要资金200×10=2000（元），而剩余资金为2000－500=1500＜2000，

所以资金不够用。　

6、（1）的坐标（-9，-1）， 图略；（2）的坐标（5，5）， 图略；（3）图略

7、结论: AE∶AC=1∶(1+n)时,

AO∶AD=2∶(2+n)．

证明:如图4,作DF∥BE,交AC于F．

∵BD=DC,∴EF=FC．

∵AE∶AC=1∶(1+n),∴AE∶EC=1∶n=2∶2n．

∴AE∶EF=2∶n．

∴AO∶AD=AE∶EF=2∶(2+n)．

8、设经x秒后，△PBQ∽△BCD，由于∠PBQ=∠BCD= 90°，

（1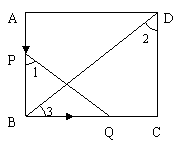）　　　 当∠1=∠2时，有：，

即；

（2）　　　 当∠1=∠3时，有：，

即

∴经过秒或2秒，△PBQ∽△BCD。