配几何画板测试题
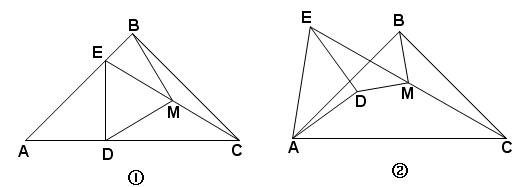
25、（12分）已知Rt△ABC中，AB=BC，在Rt△ADE中，AD=DE，连结EC，取EC中点M，连结DM和BM，
（1）若点D在边AC上，点E在边AB上且与点B不重合，如图①，求证：BM=DM且BM⊥DM；
（2）如图①中的△ADE绕点A逆时针转小于45°的角，如图②，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明。
郴州
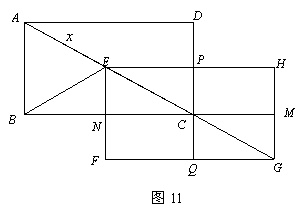
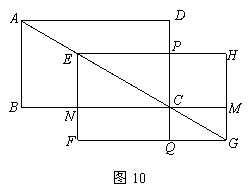
27．如图，矩形ABCD中，AB＝3，BC＝4，将矩形ABCD沿对角线AC平移，平移后的矩形为EFGH（A、E、C、G始终在同一条直线上），当点E与C重合时停止移动．平移中EF与BC交于点N，GH与BC的延长线交于点M，EH与DC交于点P，FG与DC的延长线交于点Q．设S表示矩形PCMH的面积，
表示矩形NFQC的面积．
（1） S与相等吗？请说明理由．
（2）设AE＝x，写出S和x之间的函数关系式，并求出x取何值时S有最大值，最大值是多少？
（3）如图11，连结BE，当AE为何值时，
是等腰三角形．
 | |||
 | |||
福州
如图①，以矩形ABCD的顶点A为原点，AD所在的直线为x轴，AB所在的直线为y轴，建立平面直角坐标系。点D的坐标为(8，0)，点B的坐标为(0，6)，点F在对角线AC上运动(点F不与点A、C重合)，过点F分别作x轴、y轴的垂线，垂足为G、E。设四边形BCFE的面积为S1，四边形CDGF的面积为S2，△AFG的面积为S3。
(1)试判断S1、S2的关系，并加以证明；
(2)当S3∶S2＝1∶3时，求点F的坐标；
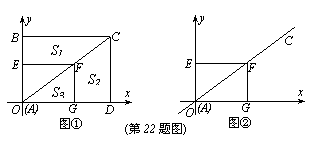(3)如图②，在(2)的条件下，把△AEF沿对角线AC所在的直线平移，得到△A’E’F’，且A’、F’两点始终在直线AC上。是否存在这样的点E’，使点E’到x轴的距离与到y轴的距离比是5∶4，若存在，请求出点E’的坐标；若不存在，请说明理由。
河北
在△ABC中，AB=AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图15-1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．
（1）在图15-1中请你通过观察、测量BF与CG的
长度，猜想并写出BF与CG满足的数量关系，
然后证明你的猜想；
（2）当三角尺沿AC方向平移到图15-2所示的位置时，
一条直角边仍与AC边在同一直线上，另一条
直角边交BC边于点D，过点D作DE⊥BA于
点E．此时请你通过观察、测量DE、DF与CG
的长度，猜想并写出DE＋DF与CG之间满足
的数量关系，然后证明你的猜想；
（3）当三角尺在（2）的基础上沿AC方向继续平
移到图15-3所示的位置（点F在线段AC上，
且点F与点C不重合）时，（2）中的猜想是否
仍然成立？（不用说明理由）
宜昌25.如图1，点A是直线y＝kx（k＞0，且k为常数）上一动点，以A为顶点的抛物线y＝(x－h)2＋m交直线y＝kx于另一点E，交 y 轴于点F，抛物线的对称轴交x轴于点B，交直线EF于点C.（点A,E,F两两不重合）
(1)请写出h与m之间的关系；（用含的k式子表示）
(2)当点A运动到使EF与x轴平行时(如图2)，求线段AC与OF的比值；
(3)当点A运动到使点F的位置最低时(如图3)，求线段AC与OF的比值.
 |
（第25题图1）
（第25题图2）
（第25题图3）
连云港
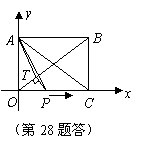
28．（本小题满分14分）如图，在直角坐标系中，矩形
的顶点
与坐标原点重合，顶点
在坐标轴上，
，
．动点
从点出发，以
的速度沿
轴匀速向点
运动，到达点即停止．设点运动的时间为
．
（1）过点作对角线
的垂线，垂足为点
．求
的长
与时间
的函数关系式，并写出自变量的取值范围；
（2）在点运动过程中，当点关于直线
的对称点
恰好落在对角线上时，求此时直线的函数解析式；
（3）探索：以
三点为顶点的
的面积能否达到矩形面积的
？请说明理由．
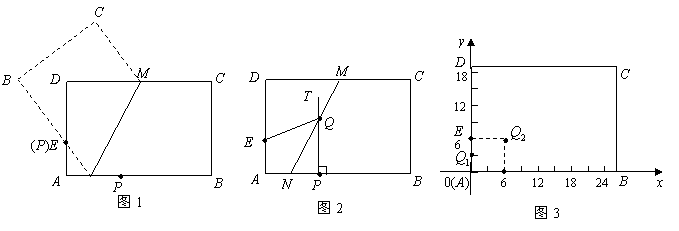
2007年福建省宁德市26．（本题满分14分）
已知：矩形纸片
中，
厘米，
厘米，点
在
上，且
厘米，点是
边上一动点．按如下操作：
步骤一，折叠纸片，使点与点重合，展开纸片得折痕
（如图1所示）；
步骤二，过点作
，交所在的直线于点
，连接
（如图2所示）
（1）无论点在边上任何位置，都有
（填“
”、“
”、“
”号）；
（2）如图3所示，将纸片放在直角坐标系中，按上述步骤一、二进行操作：
①当点在
点时，与交于点
点的坐标是（ ，
）；
②当
厘米时，与交于点
点的坐标是（ ，
）；
③当
厘米时，在图3中画出
（不要求写画法），并求出与的交点
的坐标；
（3）点在运动过程，与形成一系列的交点
观察、猜想：众多的交点形成的图象是什么？并直接写出该图象的函数表达式．
26．（1）
．····································································································· 2分
（2）①
；②
．······························································································· 6分
③画图，如图所示．······································································································ 8分
解：方法一：设
与
交于点
．
在
中，
，
．
，
，
．
又
，
．
．
．
．·············································································································· 11分
方法二：过点
作
，垂足为
，则四边形
是矩形．
，
．
设
，则
．
在
中，
．
．
．
．
．·············································································································· 11分
（3）这些点形成的图象是一段抛物线．······································································ 12分
函数关系式：
．····································································· 14分
说明：若考生的解答：图象是抛物线，函数关系式：
均不扣分．
2007年福建省三明市26．（本小题满分12分）
如图①，②，在平面直角坐标系
中，点的坐标为(4，0)，以点为圆心，4为半径的圆与轴交于，
两点，
为弦，
，是轴上的一动点，连结
．
（1）求
的度数；（2分）
（2）如图①，当与
相切时，求
的长；（3分）
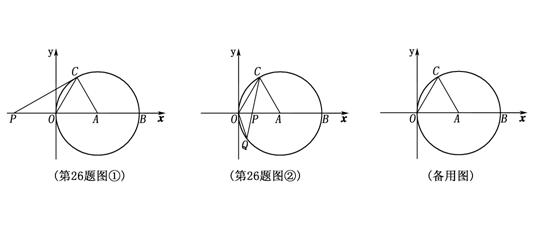（3）如图②，当点在直径上时，的延长线与相交于点，问
为何值时，
是等腰三角形？（7分）
26．解：（1）∵
，
，
∴
是等边三角形．
∴
． ··············································· 2分
（2）∵CP与相切，
∴
．
∴
．
又∵
（4，0），∴
．∴
．
∴
．
································ 5分
（3）①过点
作
，垂足为
，延长
交
于
，
∵
是半径， ∴
，∴
，
∴
是等腰三角形．···························································································· 6分
又∵是等边三角形，∴
=2 ．··························································· 7分
②解法一：过作
，垂足为
，延长
交于
，
与
轴交于
，
∵是圆心， ∴
是
的垂直平分线． ∴
．
∴
是等腰三角形， ························································································· 8分
过点作
轴于
，
在
中，∵
，
∴
．∴点的坐标（4+
，
）．
在
中，∵
，
∴
．∴点坐标（2，
）． ································································· 10分
设直线
的关系式为：
，则有
解得：
∴
．
当
时，
．
∴
． ································································································· 12分
解法二： 过A作，垂足为，延长交于，与轴交于，
∵是圆心， ∴是的垂直平分线． ∴．
∴是等腰三角形．··························································································· 8分
∵，∴
．
∵平分
，∴
．
∵是等边三角形，
， ∴
．
∴
．
∴
是等腰直角三角形．···················································································· 10分
∴
．
∴
．···················································································· 12分
2007年河池市26． （本小题满分12分）
如图12， 四边形OABC为直角梯形，A（4，0），B（3，4），C（0，4）． 点
从出发以每秒2个单位长度的速度向运动；点
从同时出发，以每秒1个单位长度的速度向运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点作
垂直轴于点，连结AC交NP于Q，连结MQ．
（1）点 （填M或N）能到达终点；
（2）求△AQM的面积S与运动时间t的函数关系式，并写出自变量t的取值范围，当t为何值时，S的值最大；
（3）是否存在点M，使得△AQM为直角三角形？若存在，求出点M的坐标，若不存在，说明理由．
 | |||||
 | |||||
| |||||
2007年河池市26． 解：（1）点 M ································································· 1分
（2）经过t秒时，
，
则
，
∵
=
=
∴
∴
································································· 2分
∴
·············································································································· 3分
∴
············································································· 5分
∵
∴当
时，S的值最大． ································································· 6分
（3）存在． ········································································································· 7分
设经过t秒时，NB=t，OM=2t
则，
∴==
··············································································· 8分
①若
，则是等腰Rt△
底边
上的高
∴是底边的中线 ∴
∴
∴
∴点的坐标为（1，0） ·················································································· 10分
②若
，此时
与
重合
∴
∴
∴
∴点的坐标为（2，0） ·················································································· 12分
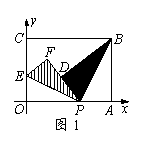
湖北省荆门市2007年28．(本小题满分12分)
如图1，在平面直角坐标系中，有一张矩形纸片OABC，已知O(0，0)，A(4，0)，C(0，3)，点P是OA边上的动点(与点O、A不重合)．现将△PAB沿PB翻折，得到△PDB；再在OC边上选取适当的点E，将△POE沿PE翻折，得到△PFE，并使直线PD、PF重合．
(1)设P(x，0)，E(0，y)，求y关于x的函数关系式，并求y的最大值；
(2)如图2，若翻折后点D落在BC边上，求过点P、B、E的抛物线的函数关系式；
(3)在(2)的情况下，在该抛物线上是否存在点Q，使△PEQ是以PE为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标．
湖北省荆门市2007年28．解：(1)由已知PB平分∠APD，PE平分∠OPF，且PD、PF重合，则∠BPE=90°．∴∠OPE＋∠APB=90°．又∠APB＋∠ABP=90°，∴∠OPE=∠PBA．
∴Rt△POE∽Rt△BPA．……………………………………………………………………2分
∴
．即
．∴y=
(0＜x＜4)．
且当x=2时，y有最大值
．………………………………………………………………4分
(2)由已知，△PAB、△POE均为等腰三角形，可得P(1，0)，E(0，1)，B(4，3)．……6分
设过此三点的抛物线为y=ax2＋bx＋c，则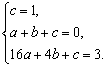
∴
y=
．……………………………………………………………………………8分
(3)由(2)知∠EPB=90°，即点Q与点B重合时满足条件．………………………………9分
直线PB为y=x－1，与y轴交于点(0，－1)．
将PB向上平移2个单位则过点E(0，1)，
∴该直线为y=x＋1．………………………………………………………………………10分
由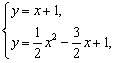
得
∴Q(5，6)．
故该抛物线上存在两点Q(4，3)、(5，6)满足条件．……………………………………12分
泰州市2007年29．如图①，
中，
，
．它的顶点的坐标为
，顶点的坐标为
，
，点从点出发，沿
的方向匀速运动，同时点从点
出发，沿轴正方向以相同速度运动，当点到达点时，两点同时停止运动，设运动的时间为秒．
（1）求
的度数．
（2）当点在上运动时，
的面积
（平方单位）与时间（秒）之间的函数图象为抛物线的一部分，（如图②），求点的运动速度．
（3）求（2）中面积与时间之间的函数关系式及面积取最大值时点的坐标．
（4）如果点
保持（2）中的速度不变，那么点沿边运动时，
的大小随着时间的增大而增大；沿着
边运动时，的大小随着时间的增大而减小，当点沿这两边运动时，使
的点有几个？请说明理由．
九、（本题满分14分）
（1）
．··································································································· 2分
（2）点的运动速度为2个单位/秒．·········································································· 4分
（3）
（
）
································································································ 6分
．
当
时，有最大值为
，
此时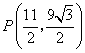
．····································································································· 9分
（4）当点沿这两边运动时，
的点有2个．····································· 11分
①当点与点重合时，
，
当点运动到与点重合时，
的长是12单位长度，
作
交轴于点，作
轴于点
，
由
得：
，
所以
，从而
．
所以当点在边上运动时，的点有1个．··································· 13分
②同理当点在边上运动时，可算得
．
而构成直角时交轴于
，
，
所以
，从而的点也有1个．
所以当点沿这两边运动时，的点有2个．······································· 14分
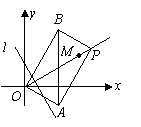
无锡市2007年28．（本小题满分10分）
如图，平面上一点从点
出发，沿射线
方向以每秒1个单位长度的速度作匀速运动，在运动过程中，以
为对角线的矩形
的边长
；过点且垂直于射线的直线
与点同时出发，且与点沿相同的方向、以相同的速度运动．
（1）在点运动过程中，试判断与轴的位置关系，并说明理由．
（2）设点与直线都运动了秒，求此时的矩形与直线在运动过程中所扫过的区域的重叠部分的面积（用含的代数式表示）．
解：（1）
轴．···························· 1分
理由：
中，
，
．····· 2分
设交于点，交轴于点，矩形的对角线互相平分且相等，则
，
，过点作
轴于，则
，
，
，
，
轴．······················· 3分
（2）设在运动过程中与射线交于点，过点且垂直于射线的直线交于点
，过点且垂直于射线的直线交于点，则
．
，
，
，
，
．
······································ 4分
①当
，即
时，
．·············· 6分
②当
，即
时，设直线交于
，交
于
，则
，
，
，
．··········· 8分
③当
，即
时，
，
………………………………………………10分
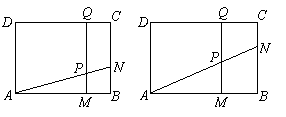
扬州市2007年26．（本题满分14分）
如图，矩形中，
厘米，
厘米（
）．动点
同时从点出发，分别沿
，
运动，速度是
厘米／秒．过作直线垂直于，分别交
，
于．当点到达终点时，点也随之停止运动．设运动时间为秒．
（1）若
厘米，秒，则
______厘米；
（2）若
厘米，求时间，使
，并求出它们的相似比；
（3）若在运动过程中，存在某时刻使梯形
与梯形
的面积相等，求
的取值范围；
（4）是否存在这样的矩形：在运动过程中，存在某时刻使梯形，梯形，梯形
的面积都相等？若存在，求的值；若不存在，请说明理由．
26．（1）
，
（2）
，使，相似比为
（3）
，
，
即
，
当梯形与梯形的面积相等，即
化简得
，
，
，则
，
（4）
时，梯形与梯形的面积相等
梯形的面积与梯形的面积相等即可，则
，把代入，解之得
，所以
．
所以，存在，当时梯形与梯形的面积、梯形的面积相等．
江西省南昌市2007年25．实验与探究
（1）在图1，2，3中，给出平行四边形的顶点
的坐标（如图所示），写出图1，2，3中的顶点的坐标，它们分别是 ， ，
；
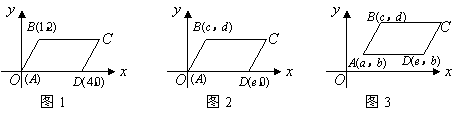
（2）在图4中，给出平行四边形的顶点的坐标（如图所示），求出顶点的坐标（点坐标用含
的代数式表示）；
归纳与发现
（3）通过对图1，2，3，4的观察和顶点的坐标的探究，你会发现：无论平行四边形处于直角坐标系中哪个位置，当其顶点坐标为
（如图4）时，则四个顶点的横坐标
之间的等量关系为
；纵坐标
之间的等量关系为
（不必证明）；
运用与推广
（4）在同一直角坐标系中有抛物线
和三个点
，
（其中
）．问当
为何值时，该抛物线上存在点，使得以
为顶点的四边形是平行四边形？并求出所有符合条件的点坐标．
25．解：（1）
，
，
．····················································· 2分
（2）分别过点
作轴的垂线，垂足分别为
，
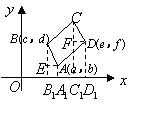分别过
作
于，
于点．
在平行四边形中，
，又
，
．
．
又
，
．·································································································· 5分
，
．
设
．由
，得
．
由
，得
．
．································ 7分
（此问解法多种，可参照评分）
（3）
，
或
，
．························· 9分
（4）若
为平行四边形的对角线，由（3）可得
．要使
在抛物线上，
则有
，即
．
（舍去），
．此时
．································································ 10分
若
为平行四边形的对角线，由（3）可得
，同理可得
，此时
．
若
为平行四边形的对角线，由（3）可得
，同理可得，此时
．
综上所述，当时，抛物线上存在点，使得以为顶点的四边形是平行四边形．
符合条件的点有，，． 12分
乐山市2007年
28．如图（16），抛物线
的图象与轴交于
两点，与轴交于点，其中点的坐标为
；直线
与抛物线交于点，与轴交于点，且
．
（1）用
表示点的坐标；
（2）求实数的取值范围；
（3）请问
的面积是否有最大值？
若有，求出这个最大值；若没有，请说明理由．
28．解（1）抛物线
过
，
·········································································································· 1分
点在抛物线上，
，
点的坐标为
．·················································································· 3分
（2）由（1）得
，
，
，
．······························································································· 6分
（3）的面积有最大值，············································································ 7分
的对称轴为
，，
点的坐标为
，··················································································· 8分
由（1）得
，
而
，······························································································ 10分
的对称轴是
，
当
时，
取最大值，
其最大值为
． 12分