中考数学第五次模拟试题
一、填空题(每小题3分,共15分)
1、在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中,是无理数的个数是( )
中,是无理数的个数是( )
A、1个 B、2个 C、3个 D、4个
2、如果![]() 是由四舍五入法得到的近似数,则它有(
)个有效数字
是由四舍五入法得到的近似数,则它有(
)个有效数字
A、6 B、5 C、4 D、3
3、在下面四种正多边形中用一种图形不能平面镶嵌的是( )
A、正三角形 B、正方形 C、正五边形 D、正六边形
|
A、![]() B、
B、![]()
C、3 D、![]()
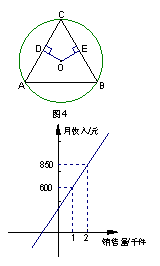
5、如图2,在平面直角坐标系中,
若![]() ~
~![]() ,那么点
,那么点![]() 的
的
坐标为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
二、填空题(每小题4分,共20分)
6、若![]() ,
,![]() ,则点
,则点![]() 应在第 象限。
应在第 象限。
7、反比例函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而增大,则
的增大而增大,则![]() =
=
|
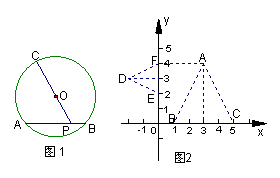
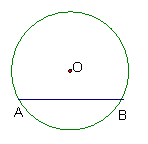
8、如图3,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 、
、![]() 是
是
弧![]() 上的三等分点,若
上的三等分点,若![]() 的半径为1,
的半径为1,![]() 为
为
线段![]() 上任意一点,则图中阴影部分的
上任意一点,则图中阴影部分的
面积为
|
![]() 为圆心,
为圆心,![]() ,
,![]() ,
,![]() 、
、
![]() 是垂足,若
是垂足,若![]() ,则
,则![]() 的面
的面
积是
![]()
10、某公司销售人员的个人月收入与其每月
的销售量成一次函数关系,如图,则此销售
人员的销售量为3千件时的月收入是 元。
三、解答题(每小题6分,共30分)
11、已知不等式![]() 的最小整数解是方程
的最小整数解是方程![]() 的解,求
的解,求![]() 的值。
的值。
12、已知:![]() ;
; ![]() ,小敏、小聪两人在
,小敏、小聪两人在![]() ,
,![]() 的条件下分别计算了
的条件下分别计算了![]() 和
和![]() 的值,小敏说
的值,小敏说![]() 的值比
的值比![]() 大,小聪说
大,小聪说![]() 的值比
的值比![]() 大,请你判断谁的结论正确,并说明理由。
大,请你判断谁的结论正确,并说明理由。
|
13、在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,
![]() 是
是![]() 上一点,若
上一点,若![]() ,求
,求![]() 的长。
的长。
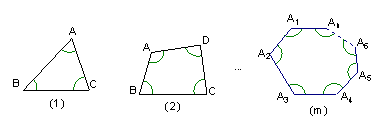
14、如图,①、②、…、⑩是边长均大于2的三角形、四边形、…、凸![]() 边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、
边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、![]() 条弧。
条弧。
⑴、图⑴中3条弧的弧长的和为
⑵、图⑵中4条弧的弧长的和为
⑶、求图(m)中![]() 条弧的弧长的和
(用
条弧的弧长的和
(用![]() 表示)
表示)
|
|
⑴、求作![]() 的一个内接
的一个内接![]() ,使
,使![]() 为
为![]()
的一边,且使![]() 与
与![]() 构成轴对称图形;
构成轴对称图形;
⑵、问题⑴中的三角形最多可以作 个。
(保留作图痕迹,不写作法)
四、解答题(每小题7分,共28分)
|
| 测试 项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
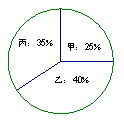
根据录用程序,该单位组织200名职工利用投票推荐的方式对三人进行民主评议,三人的得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记1 分。
⑴、请算出三人的民主评议得分;
⑵、根据上述三项的平均成绩确定录用人选,那么谁将首先被录用?(精确到![]() )
)
⑶、根据实际需要,该单位将笔试、面试、民主评议三项按得分4:3:3的比例确定个人成绩,那么谁将被录用。
17、某校共有4个大餐厅和3个小餐厅,经过测试:同时开放1 个大餐厅,2个小餐厅,可供1200人就餐;同时开放2 个大餐厅,1个小餐厅,可供1500人就餐。
⑴、求1个大餐厅, 1个小餐厅分别可供多少名学生就餐;
⑵、若7个餐厅同时开放,能否供全校3500名学生同时就餐?请说明理由。
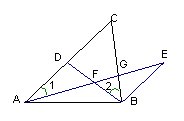
|
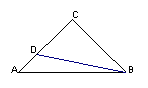
⑴、试猜想![]() 与
与![]() 有何关系?给予证明;
有何关系?给予证明;
⑵、若![]() 的面积为
的面积为![]() ,
,
求四边形![]() 的面积。
的面积。
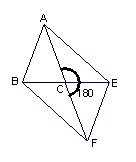
|
⑴、求![]() 的度数;
的度数;
⑵、若![]() ,且
,且![]() ,求
,求![]() 的长。
的长。
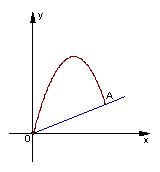
五、解答题(每小题9分,共27分)
|
⑵、网球在斜坡的落点![]() 的垂直高度。
的垂直高度。
|
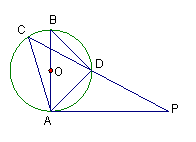
⑴、图中哪个三角形与![]() 全等?证明你的结论;
全等?证明你的结论;
⑵、探索线段![]() 、
、![]() 、
、![]() 之间的关系,
之间的关系,
并说明理由。
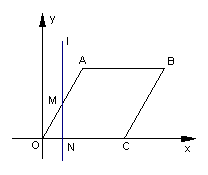
22、如图,在平面直角坐标系中,四边形![]() 为菱形,点
为菱形,点![]() 的坐标为
的坐标为![]() 、
、![]() ,垂直于
,垂直于![]() 轴的直线
轴的直线![]() 从
从![]() 轴出发,沿
轴出发,沿![]() 轴正方向以每秒1个单位长度的速度运动,设直线
轴正方向以每秒1个单位长度的速度运动,设直线![]() 与菱形
与菱形![]() 的两边分别交于点
的两边分别交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的上方)
的上方)
⑴、求![]() 、
、![]() 两点坐标;
两点坐标;
⑵、设![]() 的面积为
的面积为![]() ,直线
,直线![]() 运动时间为
运动时间为![]() 秒
秒![]() ,试求
,试求![]() 与
与![]() 的函数表达式;
的函数表达式;
⑶、在题⑵的条件下,![]() 为何值时,
为何值时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
|