中考数学专题复习5：探索性问题

中考数学专题复习5：探索性问题

Ⅰ、综合问题精讲：

探索性问题是指命题中缺少一定的条件或无明确的结论，需要经过推断，补充并加以证明的题型．探索性问题一般有三种类型：（1）条件探索型问题；（2）结论探索型问题；（3）探索存在型问题．条件探索型问题是指所给问题中结论明确，需要完备条件的题目；结论探索型问题是指题目中结论不确定，不唯一，或题目结论需要类比，引申推广，或题目给出特例，要通过归纳总结出一般结论；探索存在型问题是指在一定的前提下，需探索发现某种数学关系是否存在的题目．

　  探索型问题具有较强的综合性，因而解决此类问题用到了所学过的整个初中数学知识．经常用到的知识是：一元一次方程、平面直角坐标系、一次函数与二次函数解析式的求法（图象及其性质）、直角三角形的性质、四边形（特殊）的性质、相似三角形、解直

角三角形等．其中用几何图形的某些特殊性质：勾股定理、相似三角形对应线段成比例等来构造方程是解决问题的主要手段和途径．因此复习中既要重视基础知识的复习，又要加强变式训练和数学思想方法的研究，切实提高分析问题、解决问题的能力．

Ⅱ、典型例题剖析

【例1】（2005，临沂）如图2－6－1，已知抛物线的顶点为A(O，1)，矩形CDEF的顶点C、F在抛物线上，D、E在轴上，CF交y轴于点B(0，2)，且其面积为8．

(1)求此抛物线的解析式；

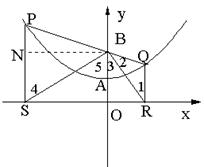
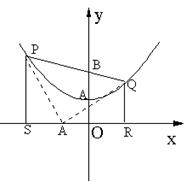
(2)如图2－6－2，若P点为抛物线上不同于A的一点，连结PB并延长交抛物线于点Q，过点P、Q分别作轴的垂线，垂足分别为S、R．

①求证：PB＝PS；

②判断△SBR的形状；

③试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似，若存在，请找出M点的位置；若不存在，请说明理由．

⑴解：方法一：∵B点坐标为(0，2)，∴OB＝2，

∵矩形CDEF面积为8，∴CF=4.

∴C点坐标为(一2，2)．F点坐标为(2，2)。

设抛物线的解析式为．

其过三点A(0，1)，C(-2．2)，F(2，2)。

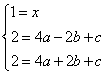得 解得

∴此抛物线的解析式为

方法二：∵B点坐标为(0，2)，∴OB＝2，

∵矩形CDEF面积为8，　　 ∴CF=4.

∴C点坐标为(一2，2)。　

根据题意可设抛物线解析式为。

其过点A(0，1)和C(-2．2)  

　解得

此抛物线解析式为

(2)解：

①过点B作BN，垂足为N．

∵P点在抛物线y=+l上．可设P点坐标为．∴PS＝，OB＝NS＝2，BN＝。∴PN=PS—NS= 在RtPNB中．

PB²＝

∴PB＝PS＝

②根据①同理可知BQ＝QR。

∴，

又∵ ，

∴，

同理SBP＝∠B  

∴

∴∴.

∴ △SBR为直角三角形．

③方法一：设，

∵由①知PS＝PB＝b．，。∴

∴。假设存在点M．且MS＝，别MR＝ 。若使△PSM∽△MRQ，

则有。即

∴。　 ∴SR＝2

∴M为SR的中点. 若使△PSM∽△QRM，

则有。∴。

∴。

∴M点即为原点O。

综上所述，当点M为SR的中点时．PSM∽ΔMRQ；当点M为原点时，PSM∽MRQ．

方法二：若以P、S、M为顶点的三角形与以Q、M、R为顶点三角形相似，

∵，

∴有PSM∽MRQ和PSM∽△QRM两种情况。

　　 当PSM∽MRQ时．SPM＝RMQ，SMP＝RQM．

由直角三角形两锐角互余性质．知PMS+QMR＝90°。∴。

取PQ中点为N．连结MN．则MN＝PQ=．

∴MN为直角梯形SRQP的中位线,

∴点M为SR的中点　 当△PSM∽△QRM时，

。又，即M点与O点重合。∴点M为原点O。

综上所述，当点M为SR的中点时，PSM∽△MRQ；当点M为原点时，PSM∽△QRM。

　　　 点拨：通过对图形的观察可以看出C、F是一对关于y轴的对称点，所以（1）的关键是求出其中一个点的坐标就可以应用三点式或 y=ax²+c型即可．而对于点 P既然在抛物线上，所以就可以得到它的坐标为（a，a²+1）．这样再过点B作BN⊥PS．得出的几何图形求出PB 、PS的大小．最后一问的关键是要找出△PSM与△MRQ相似的条件．

【例2】探究规律：如图2－6－4所示，已知：直线m∥n，A、B为直线n上两点，C、P为直线m上两点．

 （1）请写出图2－6－4中，面积相等的各对三角形；

 （2）如果A、B、C为三个定点，点P在m上移动，那么，无论P点移动到任何位置，总有________与△ABC的面积相等．理由是：_________________.

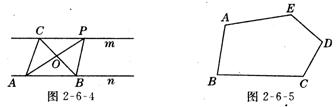
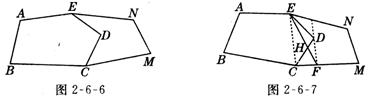
　　  解决问题：如图 2－6－5所示，五边形 ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图2－6－6所示的形状，但承包土地与开垦荒地的分界小路（2－6－6中折线CDE）还保留着；张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多，右边的土地面积与开垦的荒地面积一样多．请你用有关的几何知识，按张大爷的要求设计出修路方案（不计分界小路与直路的占地面积）．

　（1）写出设计方案．并画出相应的图形；

　（2）说明方案设计理由．

解：探究规律：（l）△ABC和△ABP，△AOC和△ BOP、△CPA和△CPB．

　　（2）△ABP；因为平行线间的距离相等，所以无论点P在m上移动到任何位置，总有△ABP与△ABC同底等高，因此，它们的面积总相等．

　解决问题：⑴画法如图2－6－7所示．

　连接EC，过点D作DF∥EC，交CM于点F，连接EF，EF即为所求直路位置．

　  ⑵设EF交CD于点H，由上面得到的结论可知：

　S_ΔECF=S_ΔECD，S_ΔHCF=S_ΔEDH，所以_{S五边形ABCDE}=S_{五边形ABCFE}，S_{五边形EDCMN}=S_{四边形EFMN}．

　 　 点拨：本题是探索规律题，因此在做题时要从前边问题中总结出规律，后边的问题要用前边的结论去一做，所以要连接EC，过D作DF∥EC，再运用同底等高的三角形的面积相等．

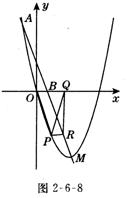【例3】（2005，成都模拟，12分）如图2－6－8所示，已知抛物线的顶点为M（2，－4），且过点A(－1,5)，连结AM交x轴于点B．

⑴求这条抛物线的解析式；

⑵求点 B的坐标；

⑶设点P（x，y）是抛物线在x轴下方、顶点 M左方一段上的动点，连结 PO，以P为顶点、PQ为腰的等腰三角形的另一顶点Q在x轴上，过Q作x轴的垂线交直线AM于点R，连结PR．设面 PQR的面积为S．求S与x之间的函数解析式；

⑷在上述动点P（x，y）中，是否存在使S_ΔPQR=2的点？若存在，求点P的坐标；若不存在，说明理由．

解：（1）因为抛物线的顶点为M（2，－4）

所以可设抛物线的解析式为y=（x－2）² －4．

因为这条抛物线过点A（－1，5）

所以5=a(－1－2)²－4．解得a=1．

所以所求抛物线的解析式为y=（x—2）² －4

（2）设直线AM的解析式为y=kx+ b．

因为A（－1，5）, M（2，－4）

所以，

解得 k=－3，b=2．

所以直线AM的

解析式为 y=3x＋2．

当y=0时，得x= ，即AM与x轴的交点B（,0）

（3）显然，抛物线y=x²－4x过原点(0，0〕

当动点P（x，y）使△POQ是以P为顶点、PO为腰且另一顶点Q在x轴上的等腰三角形时，由对称性有点 Q（2x，0）

因为动点P在x轴下方、顶点M左方，所以0＜x＜2．

因为当点Q与B（，0）重合时，△PQR不存在，所以x≠，

所以动点P（x，y）应满足条件为0＜x＜2且x≠，

因为QR与x轴垂直且与直线AM交于点R，

所以R点的坐标为（2x，－6x+2）　　

如图2－6－9所示，作P H⊥OR于H，

则PH=　　

而S=△PQR的面积=QR·P H=

下面分两种情形讨论：

①当点Q在点B左方时，即0＜x＜时，

当R在 x轴上方，所以－6x＋2＞0．

所以S=（－6x＋2）x=－3x²+x；

②当点Q在点B右方时，即＜x＜2时

点R在x轴下方，所以－6x＋2＜0．

所以S=[－（－6x＋2）]x=3x²－x；　　

即S与x之间的函数解析式可表示为

（4）当S=2时，应有－3x²+x =2，即3x² －x+ 2=0，

显然△＜0，此方程无解．或有3x²－x =2，即3x² －x－2=0，解得x₁ =1，x₂＝－

当x=l时，y= x²－4x=－3，即抛物线上的点P（1，－3）可使S_ΔPQR=2；

当x=－＜0时，不符合条件，应舍去．

所以存在动点P，使S_ΔPQR=2，此时P点坐标为(1,－3)

点拨：此题是一道综合性较强的探究性问题，对于第（1）问我们可以采用顶点式求得此抛物线，而（2）中的点B是直线 AM与x轴的交点，所以只要利用待定系数法就可以求出直线AM，从而得出与x轴的交点B．(3)问中注意的是Q点所处位置的不同得出的S与x之间的关系也随之发生变化．（4）可以先假设存在从而得出结论．

Ⅲ、综合巩固练习：（100分　90分钟）

1．　观察图2－6－10中⑴）至⑸中小黑点的摆放规律，并按照这样的规律继续摆放．记第n个图中小黑点的个数为y．解答下列问题：

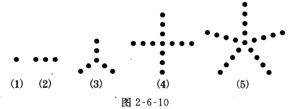
⑴ 填下表：

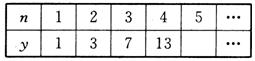
⑵ 当n=8时，y=___________；

⑶ 根据上表中的数据，把n作为横坐标，把y作为纵坐标，在图2－6－11的平面直角坐标系中描出相应的各点（n，y），其中1≤n≤5；

⑷ 请你猜一猜上述各点会在某一函数的图象上吗？

如果在某一函数的图象上，请写出该函数的解析式．

2．（5分）图2－6－12是某同学在沙滩上用石子摆成的小房子．观察图形的变化规律，写出第n个小房子用了_____________块石子．

　　　　　　 

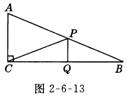
3．(10分)已知Rt△ABC中，AC=5，BC=12，∠ACB =90°，P是AB边上的动点（与点A、B不重合），Q是BC边上的动点（与点B、C不重合）．

⑴ 如图2－6－13所示，当PQ∥A C，且Q为BC的中点时，求线段CP的长；

⑵ 当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围，若不可能，请说明理由．

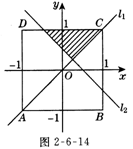
4．如图2－6－14所示，在直角坐标系中，以A（－1，－1），B（1，－1），C（1，1），D（－1，l）为顶点的正方形，设正方形在直线：y=x及动直线：y=－x+2a（－l≤a＜1）上方部分的面积为S（例如当a取某个值时，S为图中阴影部分的面积），试分别求出当a=0，a=－1时，相应的S的值．

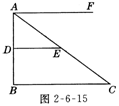
5．（10分）如图2－6－15所示，DE是△ABC的中位线，∠B＝90^○，AF∥B C．在射线A F上是否存在点M，使△MEC与△A DE相似？若存在，请先确定点M，再证明这两个三角形相似；若不存在，请说明理由．

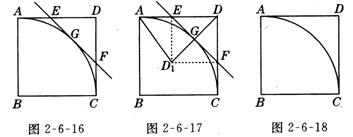
6．如图2－6－16所示，在正方形ABCD中，AB=1，是以点B为圆心．AB长为半径的圆的一段弧点E是边AD上的任意一点（点E与点A、D不重合），过E作AC所在圆的切线，交边DC于点F石为切点．

⑴ 当 ∠DEF＝45^○时，求证点G为线段EF的中点；

⑵ 设AE=x， FC=y，求y关于x的函数解析式；并写出函数的定义域；

⑶ 图2－6－17所示，将△DEF沿直线EF翻折后得△ D₁EF，当EF=时，讨论△AD₁D与△ED₁F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由。（图2－6－18为备用图）

7．（10分）取一张矩形的纸进行折叠，具体操作过程如下：

　 第一步：先把矩形ABCD对折，折痕为MN，如图　 2－6－19（1）所示；

　

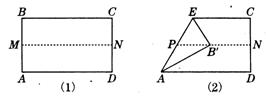
　 第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点B′，得 Rt△AB′E，如图2－6－19（2）所示；

　 第三步：沿EB′线折叠得折痕EF，如图2－6－19⑶所示；利用展开图 2－6－19（4）所示探究：

　（l）△AEF是什么三角形？证明你的结论．

　（2）对于任一矩形，按照上述方法是否都能折出这种三角形？请说明理由．

8．（10分）某校研究性学习小组在研究有关二次函数及其图象性质的问题时，发现了两个重要结论．一是发现抛物线y=ax²+2x+3(a≠0)，当实数a变化时，它的顶点都在某条直线上；二是发现当实数a变化时，若把抛物线y=ax²+2x+3(a≠0)的顶点的横坐标减少，纵坐标增加，得到A点的坐标；若把顶点的 横坐标增加，纵坐标增加，得到B点的坐标，则A、B两点一定仍在抛物线y=ax²+2x+3(a≠0)上．

⑴ 请你协助探求出实数a变化时，抛物线y=ax²+2x+3(a≠0)的顶点所在直线的解析式；

⑵ 问题⑴中的直线上有一个点不是该抛物线的顶点，你能找出它来吗？并说明理由；

⑶ 在他们第二个发现的启发下，运用“一般→特殊→一般”的思想，你还能发现什么？你能用数学语言将你的猜想表述出来吗？你的猜想能成立吗？若能成立，请说明理由。

9．已知二次函数的图象过A（－3，0），B（1，0）两点．

⑴ 当这个二次函数的图象又过点以0，3）时，求其解析式；

⑵ 设⑴中所求 M次函数图象的顶点为P，求S_ΔAPC：S_ΔABC的值；

⑶ 如果二次函数图象的顶点M在对称轴上移动，并与y轴交于点D，S_ΔAMD：S_ΔABD的值确定吗？为什么？

10．（13分）如图2－6－20所示，在 Rt△ABC中，∠ACB＝90°，BC的垂直平分线DE，交 BC于 D，交AB于E，F在DE上，并且A F＝CE．

⑴ 求证：四边形ACEF是平行四边形；

⑵ 当∠B的大小满足什么条件时，四边形A CEF是菱形？请回答并证明你的结论；

⑶ 四边形ACEF有可能是正方形吗？为什么？