中考第二次模拟数学试题卷
考试时间100分钟 满分120分
一、选择题（每题3分，共30分）
1.－8的立方根是（ ）
A. －2
B. 2
C. ±
D. －
2.下列事件中是必然事件的是（ ）
A. 杭州市2006年7月1日最高气温35℃.
B. 每年的清明节一定下雨.
C. 今年冬至这天是晴天的话，到明年正月初一肯定下雨或雪.
D. 杭州市夏季平均气温高于冬季平均气温.
3.下列式子中正确的是（ ）
A. 
B. 
C. 
D. －(－a＋b)= a＋b
4.不等式组
的最小整数解是（ ）
A. －1 B. 0 C. 1 D. 2
5.钟表上12时15分的时候，时针与分针的夹角为（ ）
A. 90° B. 82.5° C. 67.5° D. 60°
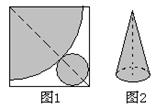6. 如图1，在正方形纸片上剪下一个圆形和一个扇形，使之恰好围成图2所示的圆锥模型，则圆的半径r与扇形的半径R之间的关系为（ ）
A. 
B . 
C. 
D. 
7. 化简
，结果正确的是（ ）
A.
B. 
C.
D. 
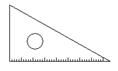8. 只用一块带有刻度的三角板（如图），（1）可以画出两条平行线；
（2）可以画出一个角的平分线；（3）可以确定一个圆的圆心. 以上三个判断中正确的个数是（ ）
A. 0 B. 1 C. 2 D. 3
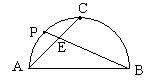9. 如图， AB是半圆的直径，点C是弧AB的中点，点P是弧AC的中点，连结PB、CA交于点E，则
=（ ）
A.
B. 
C. 
D. 
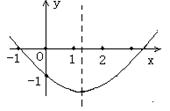10. 二次函数
的图象如图所示，有以下结论：
① a与b同号； ② y=－1时，x的值只有一个；
③ 当x=0和x=2时，函数值相等； ④ 4a＋b＞0.
其中正确结论的个数是（ ）
A. 0 B. 1 C. 2 D. 3
二、
填空题（每题4分，共24分）
11.如图，在点A和点B之间，表示整数的点有 个
12.某十字路口的交通信号灯红、绿、黄三种颜色，亮灯时间分别为红灯60秒，黄灯5秒，绿灯25秒，以此循环. 当你骑车到这个路口抬头看信号灯时，看到是红灯亮的概率是 .
13.若圆周角α所对的弦长为2sinα，则此圆的半径为
.
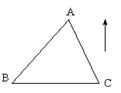
14.如右图，在△ABC中，BC边不动，点A竖直向上运动，∠A越来越小，∠B、∠C越来越大. 若∠A减少x度，∠B增加y度，∠C增加z度，则x、y、z三者之间的等量关系是 .
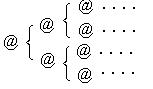15.某种细胞，每隔20分钟分裂一次，（每1个分裂成2个，见右边示意图），根据规律可得：（1）这样的一个细胞经过100分钟后可分裂成 个细胞；（2）这样的一个细胞经过n小时后可分裂成 个细胞（n是整数）.
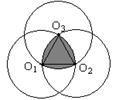16. 如图，分别以等边△O1O2O3的三个顶点为圆心，以其边长2为半径，作出三个两两相交的相同的圆，这时，这三个圆相交部分的面积是
.
三、解答题（共66分. 应写出文字说明，证明过程或演算步骤）
17.（本小题满分6分）
如图，已知AB∥DE，AB=DE， AF=DC，请问，
图中全等三角形有几对？把它们全写出来，不必证明.
18.（本小题满分6分）
写一个一元二次方程，要求二次项系数不为1，且其两根互为倒数, 并把这两根也写出来.
19.（本小题满分6分）
某班40名学生一次语文测试成绩（最高99分，分数是整数），按10分的组距分段，每个分数段学生成绩出现的频数分布表和频数分布直方图如下：
频数分布表：
| 成绩段 | 49.5 ~~59.5 | 59.5 ~~69.5 | 69.5 ~~79.5 | 79.5 ~~89.5 | 89.5 ~~99.5 |
| 频 数 | 2 | 9 | 14 | 5 | |
| 频 率 | 0.050 | 0.225 | 0.250 | 0.350 |
（1）请把频数分布表和频数分布直方图补充完整；
（2）计算这次考试的及格率（60分以上包含60分为及格）、
优秀率（90分以上包含90分为优秀）各是多少？
20. (本小题满分8分)
如图，平面直角坐标系中，△ABC是边长为3的正三角形，其中点B的坐标为（－4，1），点C的坐标为（－1，1），请按下列要求进行操作和探索：
(1)以y轴为对称轴作△ABC的对称图形△A1B1C1,（不写作法,保留作图痕迹）；
(2)以x轴为对称轴作△A1B1C1的对称图形△A2B2C2,（不写作法,保留作图痕迹）；
(3)直接写出点B1 、A2的坐标；
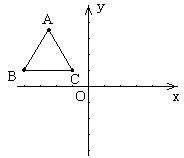(4)探索：能否通过一次旋转将△ABC旋转到△A2B2C2的位置？你若认为能，请作出肯定回答，并指出这时的旋转中心和旋转的角度；你若认为不能，请作出否定回答（不必说明理由）.
21. (本小题满分8分)
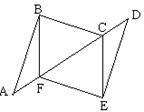
如图，已知□ABCD中，E为AD的中点，CE的延长线交BA的延长线于点F，
（1） 求证：CD=FA；
（2）
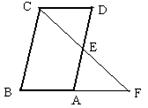若使∠F=∠BCF，□ABCD的边长之间还需要加一个什么条件？请你补上这个条件，并证明.（不要再添辅助线）
22. (本小题满分8分)
在平面直角坐标系中，A点坐标为（0，4），C点坐标为（10，0），
（1） 如图1，若直线AB∥OC，AB上有一动点P，当PO=PC时，求P点的坐标；
（2） 如图2，若直线AB与OC不平行，AB所在直线y=－x＋4上是否存在点P，
使∠OPC=90°，若有这样的点P，求出它的坐标，若没有，请简要说明理由.
23. (本小题满分12分)
某厂生产流水线要招聘操作工和包装工150人，操作工和包装工的月基本工资分别为1000元和600元，（1）现要求操作工的人数不少于包装工人数的2倍，问：操作工和包装工各招聘多少人时，可使每月所付的基本工资总额最小，最小值是多少？（2）在上述招聘两类员工月基本工资总额最小的条件下，工厂另增加10万元奖金，其中包装工奖金不大于操作工的奖金，但不低于200元，若以百元为单位发放奖金，问：有几种奖励方案？把它们都写出来.
24. (本小题满分12分)
OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴上，点C在y轴上，OA=10，OC=6.
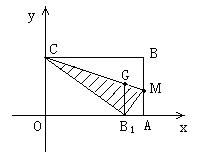（1）如图，在AB上取一点M，使得△CBM沿CM翻折后，点B落在x轴上，记作B1点，求B1点的坐标；
（2） 求折痕CM所在直线的解析式；
（3） 作B1G∥AB交CM与点G，若以C为顶点的抛物线过点G，求此抛物线的解析式.