《有理数》测试题
一 填空题（每小题4分，共20分）:
1．下列各式－12，
，0，（－4）２，－｜－5｜，－（＋3.2），
，0.815的计算结果，是整数的有________________，是分数的有_________________，是正数的有_________________，是负数的有___________________；
２．a的相反数仍是a，则a＝______；
３．a的绝对值仍是－a，则a为______；
４．绝对值不大于２的整数有_______；
５．700000用科学记数法表示是_ __，近似数9.105×104精确到_ _位，有___有效数字．
二 判断正误（每小题3分，共21分）：
1．0是非负整数………………………………………………………………………（ ）
2．若a＞b，则a＞b……………………………………………………………（ ）
3．23＝32………………………………………………………………………………（ ）
4．－73＝（－7）×（－7）×（－7）……………………………………………（ ）
5．若a是有理数，则a2＞0…………………………………………………………( )
6. 若a是整数时，必有an≥0(n是非0自然数) …………………………………………( )
7. 大于－1且小于0的有理数的立方一定大于原数……………………………………( )
三 选择题（每小题4分，共24分）：
１．平方得4的数的是…………………………………………………………………（ ）
（A）2 （B）－2 （C）2或－2 （D）不存在
２．下列说法错误的是…………………………………………………………………（ ）
（A）数轴的三要素是原点，正方向、单位长度
（B）数轴上的每一个点都表示一个有理数
（C）数轴上右边的点总比左边的点所表示的数大
（D）表示负数的点位于原点左侧
３．下列运算结果属于负数的是………………………………………………………（ ）
（A）－（1－98×7） （B）（1－9）8－17
（C）－（1－98）×7 （D）1－（9×7）（－8）
４．一个数的奇次幂是负数，那么这个数是…………………………………………（ ）
（A）正数 （B）负数 （C）非正数 （D）非负数
５．若ab＝ab，必有………………………………………………………………（ ）
（A）ab不小于0 （B）a，b符号不同 （C）ab＞0 （D）a＜0 ，b＜0
６．－
，－0.2，－0.22三个数之间的大小关系是……………………………（ ）
（A）－＞－0.2＞－0.22
（B）－＜－0.2＜－0.22
（C）－＞－0.22＞－0.2 （D）－0.2＞－0.22＞－
四 计算（每小题7分，共28分）：
１．（－
）×（－4）2－0.25×(－5)×(－4)3；
２．－24÷(－2
)×2＋5
×(－
)－0.25；
３．
；
４．(
)×(－18)＋1.95×6－1.45×0.4．
五 （本题7分）
当
，
时，求代数式3（a＋b）2－6ab的值．
一、答案：1、－12，0，（－4）２，－｜－5｜，；
，－（＋3.2），0.815；
（－4）２，，0.815；
－12，－｜－5｜，－（＋3.2）．
2、答案：0．
解析：应从正数、负数和0 三个方面逐一考虑再作判断．结果应为a＝0
3、答案：负数或0．
解析：应从正数、负数和0 三个方面逐一考虑再作判断．结果应为负数．
4、答案：0，±1，
2．
解析：不大于２的整数包括2，不小于－２的整数包括－2，所以不应丢掉2．
5、答案：7×105；十；4个．
解析：
700000＝7×100000＝7×105；9.105×104＝9.105×1000＝91050，所以是精确到十位；最后的0前的数字5直到左面第一个不是0的数字9，共有4个数字，所以有4个有效数字．
二、1、答案：√
解析：0既是非负数，也是整数．
2、答案：×
解析：不仅考虑正数，也要考虑负数和0 ．当a＝0，b＜0 时，或a＜0且b＜0时，
a＞b都不成立．
3、答案：×
解析：23＝2×2×2＝8，32＝3×3＝9，所以23
32
4、答案：×
解析：－73不能理解为－7×3．
5、答案：×
解析：不能忘记0．当a＝0时，a2 ≯0．
6、答案：×
解析：注意，当a＜0时，a的奇次方是负数，如（－3）3 ＝－27＜0．
7、答案：√
解析：
大于－1且小于0的有理数的绝对值都是小于1的正数，它们的乘积的绝对值变小；又，大于－1且小于0的有理数的立方一定是负数，所以大于－1且小于0的有理数的立方一定大于原数．
三、1、答案：C．
解析：平方得4的数不仅是2，也不仅是－2，所以答2或－2才完整．
2、答案：B．
解析：
虽然每一个有理数都可以用数轴上唯一的一个点来表示，但是数轴上的每一个点不都表示一个有理数．
3、答案：B.
解析：
负数的相反数是正数，所以（A）和（C）是正数；“减去负数等于加上它的相反数（正数）”所以（D）也是正数；只有（B）：（1－9）8－17 ＝－8×8－17 ＝－64－17 ＝－81．可知只有（B）正确．
4、答案：B．
解析：正数的奇次幂是正数，0的奇次幂是0，所以（A）、（C）（D）都不正确．
5、答案：A．
解析：
（B）显然不正确；（C）和（D）虽然都能使ab＝ab成立，但ab＝ab成立时，（C）和（D）未必成立，所以（C）和（D）都不成立．
6、答案：D．
解析：
比较各绝对值的大小．由于
≈0.23，所以有＞
＞
，则有－0.2＞－0.22＞－．
四、1、答案：－90．
解析：注意运算顺序，且0.25 ＝
．
（－）×（－4）2－0.25×(－5)×(－4)3
＝（－）×16－0.25×(－5)×(－64)
＝（－5）×2－（－16）×(－5)
＝－10－80
＝－90．
应注意，计算－10－80 时应看作－10 与－80 的和．
2、答案：10
．
解析：注意－24＝－2×2×2×2 ＝－16，再统一为分数计算：
－24÷(－2)×2＋5×(－)－0.25
＝－16÷(－
)×2＋
×(－)－
＝－16×(－
)×2＋（－
）－
＝ 12＋（－
）
＝ 12－
＝
．
3、答案：50．
解析：注意统一为真分数再按括号规定的顺序计算：
＝ 
＝ 
＝ 
＝ 
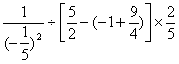
＝ 25×2
＝ 50．
注意分配律的运用．
4、答案：17.12.
解析：注意分配律的运用，可以避免通分．
()×(－18)＋1.95×6－1.45×0.4
＝ 14－15＋7＋11.7－0.58
＝ 6＋11.12
＝ 17.12．
五、答案：
．
解析：3（a＋b）2－6ab
＝ 3
（－1
＝ 3（－
）2－6
＝ 3×
－
＝ .