中考数学辅导之—圆和圆的位置关系

中考数学辅导之—圆和圆的位置关系

一、教材简析

　　本单元主要研究圆和圆的位置关系，内容主要包括两个圆各种不同位置关系的概念；相交、相切两圆的性质以及两个圆的公切线。其中两个圆不同位置关系的概念及相交、相切时的性质是本单元的重点。

　　同学们在学习过程中要注意与前面所学的圆的有关知识的联系。当一条直线 与两个圆相切时，这条直线就是这两个圆的公切线，而对于每一个圆来说，这条直线都是他们的切线。因此，研究两圆的公切线问题，就是圆的切线的判定和性质在两个相关的圆中的应用。由圆的轴对称性可以推出，任意两个圆组成的图形，一定是以连心线为轴的对称图形。两圆相交、相切的性质，都是由这个对称性得到的。所以在学习这一单元时，要随时复习巩固前面所学知识，并逐步学会运用这些知识来解决两圆位置关系中的新问题。

　　本单元学习过程中，涉及实际应用的问题较多，有计算题，也有作图题，要学会把实际问题抽象成数学问题，在关于两圆公切线长的计算中，要学会把它转化为解直角三角形的问题。

二、基本内容及应注意的问题

1、　圆和圆的位置关系的分类，既考虑了数(两圆公共点的个数)，又考虑了形(两圆的相对位置)，两圆的五种位置关系按公共点的个数(0，1，2)可分为三类：

(1)没有公共点相离　外离

　　　　　　　　　　   内含(包括同心)；

(2)有1个公共点相切 外切

　　　　　　　　　　　  内切；

(3)有2个公共点相交

2、　与点和圆、直线和圆的位置关系相类似，两圆的位置关系(形的关系)与两圆的半径、圆心距的大小(数量关系)有关。

(1)两圆外离d＞R＋r

(2)两圆外切d＝R＋r

(3)两圆相交R－r＜d＜R＋r(R≥r)

(4)两圆内切d＝R－r(R＞r)

(5)两圆内含d＜R－r(R＞r)

这个结论是双向的，“ ”是由两圆位置的关系，得到两圆半径与圆心距之间特定的数量关系，这是两圆位置关系的性质，利用这些性质可以把形的问题转化为数的问题来解决；“ ”是根据两圆半径与圆心距之间的某种数量关系来判定两圆的位置关系，从而把判定形的问题，转向为数的问题来解决。这在解决两圆的位置关系的问题时特别方便。

应当注意的是，判定两圆相交时，必须具备R－r＜d＜R＋r的条件。这是因为只有当d＞R－r时，两圆可能相交、外切或外离；而当d＜R＋r时，两圆可能相交、内切或内含。因此，只有当R－r＜d＜R＋r时才能判定两圆相交。

3、　两圆的五种位置关系中，重点讨论了两圆相交、相切的性质，在解决两圆的相交问题时，如图(1)，常添连心线、公共弦等辅助线，这样，两圆半径、圆心距、公共弦长的一半就集中到了中，可以利用三角形有关知识加以解决。

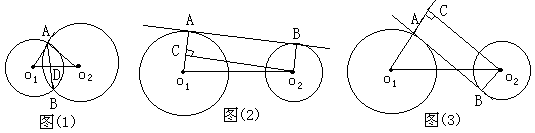
　　4、求两圆的内、外公切线长的问题，都是利用直线和圆相切的性质，通过作出过切点的半径，把问题转化为解一个直角三角形。

在图(2)、图(3)中，o₁o₂＝d，⊙o₁半径为R，⊙o₂的半径为r，则在中：

图(2)：

图(3)：

当两圆外切时，d＝R＋r，此时

外公切线长＝

5、　当两圆相交、外切、外离时，总有两条外公切线，且这两条外公切线长相等。如果两圆相等，那么两条外公切线平行；如果两圆不等，那么两条外公切线相交，且交点在两圆的连心线上。当两圆相切时，常作两圆的公切线为辅助线。

三、例题

例1、　　 已知两圆的半径R，r(R≥r)是方程的两个根，两圆的圆心距为d，

(1)若d＝4，试判定两圆的位置关系；

(2)若d＝2，试判定两圆的位置关系；

(3)若两圆相交，试确定d的取值范围；

(4)若两圆相切，求d的值。

解：∵R，r是方程的两根

∴R＋r＝3，R·r＝1

则，

(1)∵d＝4　　　　∴d＞R＋r，则两圆外离；

(2)∵d＝2　　　　∴d＜R－r，则两圆内含；

(3)∵两圆相交　　  ∴R－r＜d＜R＋r，即：＜d＜3

(4)∵两圆相切　　  ∴d＝R＋r或d＝R－r，即：d＝3或d＝

注意：两圆相切有两种可能(内切或外切)

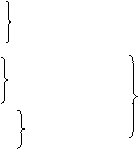
例2：如图(4)，⊙o₁与⊙o₂相交于A、B，直线Ao₁交⊙o₁于C，交⊙o₂于D，CB的延长线交⊙o₂于E，若CD＝10，DE＝6，求⊙o₂的长。

解：连结AB、AE

AC为⊙o₁的直径　

ABCD内接于⊙o₂

AE为⊙o₂的直径o₂为AE中点 　　

　　　　　　　　 o₁为AC中点

在中，　

　　　　　　  CD＝10，DE＝6

注意：两圆相交时，常添公共弦、连心线等作为辅助线，这些辅助线能把两圆中的角或线段联系起来，起到“桥梁”作用。

例3：

如图(5)，⊙o₁与⊙o₂相交于A、B，CE切⊙o₁于C，交⊙o₂于D、E

求证：

分析：因，所以只需证

，联想到两圆相交时常添的辅助线，再运用弦切角定理及圆内接四边形性质，问题易得证。

　　证：连结AB

　　　CD切⊙o₁于C　

　　　BEDA内接于⊙o₂

　　　　　 

　　　

注意：如果⊙o₁的切线CE与⊙o₂也相切于E(D、E重合)，则

成立吗？

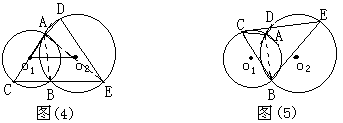
例4：如图(6)，⊙o₁与⊙o₂内切于A，过A作大圆的弦AD、AE分别交小圆于B、C。求证：

分析：要证，只需证，即要证BC∥DE；

证明：过点A作⊙o₁与⊙o₂的公切线AT，则：

　　

　　 ∵　　　 ∴BC∥DE

　　 ∴，即：

例5：如图(7)，⊙o₁与⊙o₂外切于A，BC分别切⊙o₁和⊙o₂于B、C，CA交⊙o₁于D，求证：

证明：过点A作⊙o₁、⊙o₂的公切线AE交BC于E，连结AB

EB、EA为⊙o₁的切线EB＝EA　EC＝EB＝EA

　　　　　　　  同理：EC＝EA　　　　　

BD为⊙o₁的直径　　

　　　　　　　  BC为⊙o₁的切线　　 

∽

注意：当两圆外切线内切时，公切线是常添的辅助线。

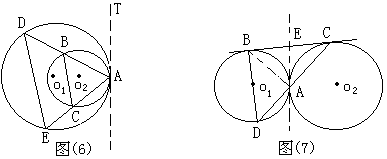
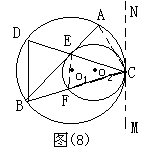
例6：如图(8)，两圆内切于点C，⊙o₁的弦AB切⊙o₂于E，CE的延长线交⊙o₁于点D，求证：

分析：要证

只须证，即要证∽，因两圆内切，所以可过点C作

公切线MN，从而证得：

又因为，从而问题得以解决。

证明：过点C作⊙o₁与⊙o₂的公切线MN，连结EF、AC，

则有：

又∵AB为⊙o₂的切线，　　∴

　∴

又∵

　∴∽　　　 ∴

即：

注：本讲内容较多，例题也比较详细、全面，因此不再单独设立练习题。