中考数学辅导之—直线和圆的位置关系(二)
一、学习目标
1、 理解切线长的概念，掌握切线长定理并会运用它解决有关问题。
2、 理解弦切角的概念，掌握弦切角定理及其推论，并会运用它们解决有关问题，通过弦切角定理的证明，进一步了解分情况证明数学命题的思想和方法。
3、 能结合具体图形，准确地表述相交弦定理、切割线定理及其推论的题设和结论，并能应用它们解有关的计算和证明题，会作两条线段的比例中项。
二、基本内容及应注意的问题
1、 “切线长”是切线上一条线段的长度，具有数量的特征；而“切线”是一条直线，它是向两方无限延展的，不可以度量长度。
2、 切线长定理包含两个结论，如图(1)所示，PA、PB切⊙O于点A、B，则有：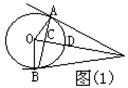
(1)“切线长相等”，即PA＝PB。
(2)“圆心和这点的连线平分两切线的夹角”，即：PO平分
；
根据PA=PB，PO平分，可得点A、B关于直线OP对称，从而有OP垂直平分AB、
＝
以及
∽
∽
等结论，由此可得，切线长定理是证明线段相等、角相等、弧相等、线段成比例，垂直关系的重要依据。
3、 讲过切线长定理以后，已知一条切线时，通常有如下五个性质可用：
(1)切线和圆有且只有一个公共点；
(2)切线和圆心的距离等于该圆的半径；
(3)切线垂直于过切点的半径；
(4)经过圆心垂直于切线的直线必过切点；
(5)经过切点垂直于切线的直线必过圆心。
若已知一个圆的两条切线相交，则又多了“切线长相等”的性质；
若已知一个圆的两条切线互相平行，则可得出“圆上两个切点的连线为直径”的性质。
4、 弦切角有两个基本特征：
(1)顶点在圆上，实际上就是角的顶点是圆的一条切线的切点；
(2)一边和圆相交，另一边和圆相切，实际上就是角的一边是过切点的一条弦（所在的直线），角的另一边是切线上以切点为端点的一条射线。
5、 弦切角定理与圆周角定理的证明思路类似，都分三种情况，而且在证明过程中利用了圆周角的推论。在学习时一定要注意与圆周角定理对比，注意它们的内在联系。
弦切角是与圆有关的又一种角，要能在图形中准确地识别，并能正确应用弦切角定理及其推论。它给我们提供了证明角相等、弧相等的又一种方法。
6、 相交弦定理揭示了圆内两条相交弦被交点分成的两条线段的长度之间的关系。其推论是把圆内两条相交弦的位置特殊化──两弦中的一条是直径，另一条是与直径垂直的弦。利用这个推论，可以作两条已知线段的比例中项。
7、 切割线定理揭示了从圆外一点引圆的切线和割线，切线长和这点到割线与圆的交点的两条线段的长之间的关系。其推论通常又称为割线定理，它和切割线定理的关系非常密切。应用时要注意定理的条件和结论。
8、 相交弦定理、切割线定理以及它们的推论，在计算和证明中应用非常广泛，学习定理时要注意结合图形来弄清定理中所指的是哪几种线段。
三、例题
例1：如图(2)所示，
中，
，以AB为直径的⊙O交BC于点D，切线DE交AC于E。
求证：
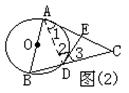
分析：连结AD，则
，要证，只需证AE=EC。
证明：连结AD
ÞAE为⊙O的切线 ÞEA=EDÞ
DE为⊙O的切线
Þ
AB为⊙O的直径Þ
Þ 
Þ DE=EC ÞDE=EA=ECÞ
EA=ED
例2、如图(3)所示，PA、PB是⊙O的切线，A、B为切点，PQ⊥OQ于Q，交AB于M
求证：OA2=OM·OQ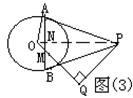
证明:连结OP交AB于N
PA、PB是⊙O的切线Þ PA=PB ÞOP⊥AB
OP平分∠APB
PA切⊙O于A Þ OA⊥PA
Þ△OAN∽△OPAÞ
ÞOA2=OP·ON
PQ⊥OQ,OP⊥ABÞ∠Q=∠ONM=90O
∠NOM=∠QOP Þ△OMN∽△OPQÞ
ÞON·OP=OM·OQ
OA2=OP·ON ÞOA2=OM·OQ
注:遇到从一点出发的两条切线,常想到切线长定理及图(1)所示的基本图形，这个基本图形中隐含了等腰三角形，全等三角形，相似三角形等条件。
例3：已知，AB为⊙O的直径，过B点作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于D。
(1)求证：CE2=CD·CB；
(2)若AB=BC=2
，求CE、CD的长。
分析：要证CE2=CD·CB，只需证：△CED∽△CBE。
证明：(1)连结BE，
BC是⊙O的切线Þ∠CBE=∠A
OA=OEÞ∠A=∠OEA Þ ∠CBE=∠CED
∠OEA=Þ∠DEC ∠C=∠C
Þ△CBE∽△CEDÞ
；
(2)BC为⊙O的切线
AB为直径 Þ∠ABD=90O
AB=2ÞOB=1 ÞOC=
ÞCE=-1；
BC=2 OE=1
又∵CE2=CD·CB，CB=2
∴(-1)2=2CD
则:CD=
即：CD、OE的长分别为(
)和(-1)。
注：有切线，并需寻找角的关系时，常添辅助线，从而为利用弦切角定理创造条件。
例4：如图(5)所示，⊙O是
的外接圆，
的平分线CE交AB于D，交⊙O于E，⊙O的切线EF交CB的延长线于F。
求证：AE2=AD·EF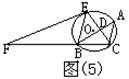
分析:连结BE，由
可得：AE=BE，所以，要证AE2=AD·EF，只需证
∽
证明：连结BE，CE平分ÞÞ
=
ÞAE=BE
=Þ∠EBD=∠ECB Þ
∠EBF=∠BEC+∠ECB EF为切线Þ
Þ
∽
Þ
ÞAE2=AD·EF
AE=BE
例5：如图(6)所示，⊙Ｏ1与⊙Ｏ2相交于点M、N，直线AE与⊙Ｏ1，⊙Ｏ2及MN顺次相交于点A，B，C，D，E。
求证:AB·CD=BC·DE
证明：由相交弦定理可得：
在⊙Ｏ1中:AC·CD=MC·NC ÞAC·CD=EC·BC
在⊙Ｏ2中:EC·BC=MC·NC
Þ(AB+BC)·CD=(CD+DE)·BCÞAB·CD+BC·CD=CD·BC+BC·DE
ÞAB·CD=BC·DE。
注：公共弦MN是沟通两个圆的线段关系的“桥梁”。
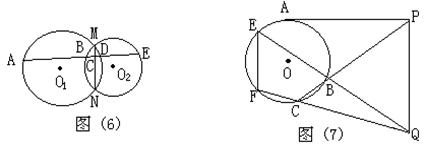
例6：如图(7)PA切⊙Ｏ于点A，PBC为⊙Ｏ的割线,PQ=PA，QB的延长线交⊙Ｏ于E，QC的延长线交圆于点F。
求证：(1)
∽
(2)PQ∥EF
分析：有切线、割线，易联想到切割线定理，故有：AP2=PB·PC，因PQ=PA，所以PQ2=PB·PC，将此式改为比例式，再加上公共角∠BPQ，易证∽。由三角形相似，可得角的相等关系，从而为证EF∥PQ创造了条件。
证明：AP为⊙O的切线 ÞAP2=PB·PC
PBC为⊙O的割线 ÞPQ2=PB·PC PQ=AP
Þ
Þ△PBQ∽△PQCÞ∠PQB=∠PCQ
∠BPQ=∠QPC Þ∠PQB=∠EÞEF∥PQ
四边形EFCB为圆内接四边形Þ∠PCQ=∠E
注：若将条件PQ=PA与结论PQ∥EF交换，命题还成立吗？请同学们自己证明。
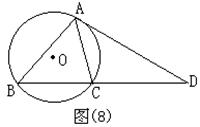
例7：如图(8)所示，△ABC内接于⊙O，DA切⊙O于点A，BC的延长线交AD于点D。
求证：
分析：由条件知：这是相似三角形的一种基本图形，易得△ADC∽△BDA，从而得：CA/AB=CD/AD=AD/DB，将此例式CA/AB=CD/AD (或
)两边平方,就符合结论的形式，再利用切割线定理的结论进行代换，命题就能得证。
证明：AD为⊙O切线Þ∠DAC=∠B Þ△DAC∽△DBA ∠D=∠D
Þ
Þ
AD为⊙O的切线 ÞAD2=DC·DB Þ
。
BCD为⊙O的割线
注：本题还可以运用面积法来证明。
四、练习及作业：
(1)已知PA、PB分别切⊙O于A、B，C是劣弧
上任意一点，过E作⊙O的切线和PA、PB分别交于D、E，若OP=5，⊙O半径为3，则
的周长为（ ）
A． 4 B．8 C．9 D．不确定
(2)圆外切四边形一组对边和为12，圆的半径为2，则这个四边形的面积为（ ）
A． 6 B．12 C．24 D．48
(3)外心、内心、垂心、重心这四心重合的三角形是（ ）
A． 任意三角形 B．直角三角形 C．等腰三角形 D．等边三角形
(4)AB、AC分别切圆于B、C，B、C两点分圆所得两弧比为1:2，则∠A的度数为（ ）
A． 45O B．90O C．60O D．120O
(5)AB、AC分别切⊙O于B、C，BC交OA于D，连结OB、OC，则圆中的直角三角形共有（ ）个
A． 3 B．4 C．5 D．6
(6)AB切⊙O于B，ACD是过O点的割线,且∠A=50O，则
的度数为（ ）
A． 50Ｏ B．140Ｏ C．90Ｏ D．280Ｏ
(7)过⊙O外一点P引圆的两切线PA、PB，A、B是切点，∠P=90Ｏ，OP=4，则⊙O半径的长为（ ）
A．
4 B．8 C．
D．
(8)⊙O的直径是AB，弦CD⊥AB于P，且CD=8，BP=2，则⊙O的半径为（ ）
A． 3 B．4 C．5 D．10
(9)BC是⊙O的直径，P是BC延长线上一点,且PC=OC，PA是⊙O的切线，且PA＝3，则⊙O半径为（ ）
A．
3 B．6 C．
D．2
(10)⊙O是△ABC的直径，P是BC延长线上一点,且PC=OC，PA是⊙O 的切线，且PA=3，则⊙O半径为 ( )
A． 40O B．140O C．80O D．70O
五、答案与提示：
1． B 2．C 3．D 4．C 5．D 6．B 7．C
8．C 9．C 10．D