中考数学模拟试卷(一)A
班级： 姓名： 座号： 成绩：
一、填空题：（每题3分，共30分）
1．
的相反数是
，
的倒数是 ．
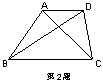
2．如图梯形ABCD中，AD//BC，对角线AC⊥BD且CD=6cm，AB=12cm，则该梯形
的中位线长等于 。
3．一次函数的图象过一、二、四象限，则它的其中一个函数表达式是 。
4．下列命题：（1）所有的等腰三角形都相似；（2）所有的等边三角形都相似；（3）所有的等腰直
角三角形都相似；（4）所有的直角三角形都相似。其中真命题的序号是： （注：把所有的真命题的序号都填上）
5．某住宅小区6月份随机抽查了该小区6天的用水量(单位：吨)，结果分别是30、34、32、37、28、31，那么，请你估计该小区6月份(30天)的总用水量约是 吨.
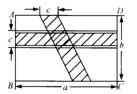
6. 如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，依照图中标注的数据，图中空白部分的面积是__________。
7、函数
的自变量
的取值范围是
。
8、已知⊙O的半径为5,弦AB的弦心距为3,则弦AB的长为 。
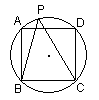
9、已知正方形内接于⊙O，P是劣弧AD上任意一点，（如图），则∠ABP+∠DCP
= 。
10、如图，P（x，y）是以坐标原点为圆心，5为半径的圆周上的点，若x，y都是
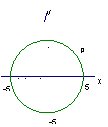整数，则这样的点共有
。
二、选择题（本题共5小题,每小题3分,共15分）
|
|
|
|
|
|
|
|
|
|
|
|
|
(C) 四个, 精确到万分位 (D) 四个, 精确到千分位
|
|
(A)
(B)
(C)3
(D)6
|
（A）66
cm2
（B）30cm2 （C）28cm2
（D）15cm2
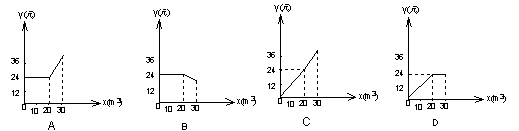14．某市为了节约用水,按以下规定收取水费;(1)每户每月用水量不超过20m3, 则每立方米水费1.2元,(2) 每户每月用水量超过20m3,则超过的部分每立方米水费2元,设某户一个月所交水费为y(元),用水量为x(m3),则y与x的函数关系用图象表示为( )
15．与函数
的图象关于x轴对称的图象的函数表达式是( )
(A)
(B)
(C) 
（D） 
三、解答下列各题（每小题6分，共24分）
16、先化简，再求值：
其中
17、已知一次函数
，当
时
的值是9，当
时的值为－3．
①求这个函数的解析式；
②在直角坐标系内画出这个函数的图象．
 |
18、已知直线l和l外的一点P，求作：
⊙P，使⊙P与直线l相切于A点。
19、为了庆祝北京申办2008年奥运会成功，某班学生计划制作240面彩旗，由于该
班有10名学生因故未能参加制作，为此该班的其余学生人均要比原计划多做4面彩旗才能完成任务，问这个班原有多少名学生？
四、解答下列各题（20、21小题各7分，22、23小题各8分，共30分）
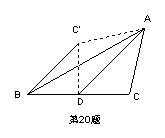20．如图：AD是△ABC的中线，∠ADC=450，把△ADC沿AD对折，点C落在
的位置，求
的
值。
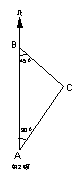21、某轮船沿正北方向航行，在A点处测得灯塔C在北偏东300，航行20海里后到达B点，在B点处测得灯塔C在南偏东450，求轮船此时距灯塔C的距离。（结果保留4个有效数字，供参考数据：
）
22、如图，二次函数
的图像与x轴交于点A（1，0）和点B（点B在点A的右侧），与y轴交于点C（0，2）。
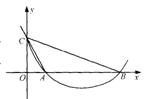（1）确定a、b、c乘积的符号，并说明理由；
（2）若∠OCA=∠CBO，求这个二次函数的解析式。
23、已知关于x的方程
有两个不相等的实数根，试判断直线
能否通过点M
，并说明为什么？
五、（24小题10分，25小题11分，共21分）
24、在初三几何第三册中我们学过一个例题：若⊙O1和⊙O2外切于点A，BC是两圆的公切线，B、C为切点，则AB⊥AC（如图1）。根据这一结论，回答下列问题，并选择其中一个问题进行证明。
（1）若两圆外切变为两圆相交，其他条件不变，猜想∠BAC＋∠BDC等于多少度？（如图2）
（2）若BC变为一圆的切线另一圆的割线，其他条件不变，则∠BAC+∠BAD等于多少度？（如图3）
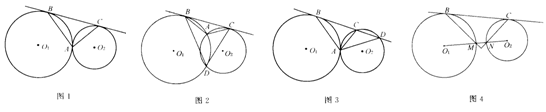（3）若两圆外切变为两圆外离，其他条件不变，连心线O1O2，分别交两圆于M、N，直线BM与CN是否垂直？（如图4）
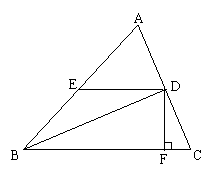25、如图，在ΔABC中，AC＝15，BC＝18，sinC=
，D是AC上一个动点（不运动至点A，C）,过D作DE∥BC，交AB于E，过D作DF⊥BC，垂足为F，连结 BD，设 CD＝x．（1）用含x的代数式分别表示DF和BF； （2）如果梯形EBFD的面积为S，求S关于x的函数关系式；
（3）如果△BDF的面积为S1，△BDE的面积为S2，那么x为何值时，S1＝2S2