中考数学辅导之—解直角三角形（相关中考题）
全国各地市中考数学试题选编(二)
----解直角三角形部分
一、填空题
1、在
则
的面积为_____。
2、在中，
，AB上的中线CE＝5，BC＝6，那么BC在AB上的射影长为_____。
3、已知角
的终边上一点P(x,2)，且sin=
，则x＝_____。
4、已知角的终边经过点P(-
,1)，则tg(1800-)＝_____。
5、在中，如果2sinC＝sin900，那么
＝_____。
6、计算：
＝_____。
7、已知角的顶点在坐标原点，始边与x轴的正半轴重合，终边经过点P(
)，则sin＝_____。
8、在Rt中，已知＝900，BC＝3,AB＝3
，那么
＝_____度。
9、在中，D、E是AB上的点，CD⊥AB，
，AD＝3，AC＝6，则BC的长是_____。
10、若ctg+1=0，且00＜＜1800，则＝_____。
11、CD是Rt的斜边AB上的高，AD＝9，DB＝4，则CD＝_____。
12、在中，若BA＝BC，
＝1200，AC＝12，则BC＝_____。
13、一个人从A点出发向北偏东600方向走了一段距离到B点，再从B点出发，向南偏西150方向走了一段距离到C点，则
的度数为_____。
14、如图1，＝900，
，利用此图求得tg750＝_____。
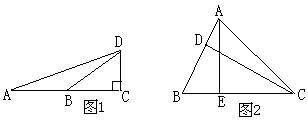
15、在直角坐标系中，角的顶点在原点，它的始边与x轴的正半轴重合，终边上一点P的坐标是(
)，那么cos＝_____。
16、若A是锐角，则
＝_____。
17、已知角的终边经过点P(-4,3)，则
＝_____。
18、在直角三角形中，若两直角边在斜边上的射影分别是4和6，则这个直角三角形的面积是_____。
19、如图2，D是的边AB上的点，且BD=2AD，若CD=4，
，那么BC边上的高AE＝_____。
二、选择题
1、在Rt中，
，下列式子中不一定成立的是：
A、sinA=sinB B、cosA=sinB C、sinA=cosB D、sin(A+B)=sinC
2、在中，已知
，则
＝：
A、
B、3
C、
D、
3、直角三角形中，自锐角顶点所引的两条中线长为5和
，那么这个直角三角形的斜边长为：
A、4
B、
C、4 D、2
4、在中，若
＜0，则：
A、A为锐角，B为钝角 B、A为钝角，B为锐角
C、A、B均为锐角 D、A、B均为钝角
5、如果
，那么等于：
A、300 B、600 C、1200 D、1500
6、若是锐角，且cos=tg300，则：
A、00＜＜300
B、300≤＜450
C、450＜＜600
D、600≤＜900
7、已知中，
，的对边长为
，的对边长为10，那么的度数为：
A、300 B、450 C、600 D、900
8、在中，a、b、c分别为
的对边的长，若
则的形状是：
A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形
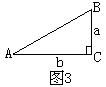
9、如图3，在Rt中，＝900，a、b分别是
的对边，如果sinA:sinB=3:2，那么a:b等于：
A、2:3 B、3:2 C、4: 9 D、9:4
10、在Rt中，＝900，a、b、c分别为角A、B、C的对边的长，若a=6,B=300，则c和tgA的值分别为：
A、
B、
C、
D、
11、若
互为补角，那么以下四个关系式中，不一定成立的是：
A、
＞0
B、cos-cos
＞0
C、
＝0
D、cos＋cos＝0
12、是直角三角形的一个锐角，
＞
则：
A、＞600 B、＜600 C、＞300 D、＜300
13、若00＜＜1800，且
，则角的度数是：
A、300 B、600 C、1500 D、300或1500
14、在中，
，AD⊥BC，若AB＝2AC，则BC与DC之间的关系为：
A、BC=2DC B、BC=3DC C、BC=4DC D、BC=5DC
15、已知Rt中，，斜边长为5，两直角边的长分别是x2-(2m-1)x+4(m-1)=0的根，则m的值等于：
A、-1 B、4 C、-4或1 D、-1或4
16、在中，，AC=1，
，那么为：
A、600 B、600或1200 C、300或1500 D、300
17、已知中，，CD是AB边上的高，则CD:CB等于：
A、sinA B、cosA C、tgA D、ctgA
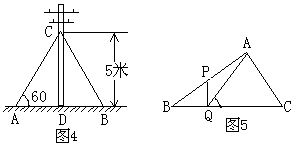
18、如图4，在离地面高度5米处引拉线固定电线杆，拉线和地面成600角，则拉线AC的长为：
A、
米 B、
米 C、
米 D、
19、如图5，在中，
，P为AB上一点，
，PQ⊥BC于Q，连结AQ，则
等于：
A、
B、
C、
D、
20、在中，若
＜0，则：
A、不可能是钝角
B、不可能是钝角
C、不可能是钝角
D、、、都不可能是钝角
21、如图6，在Rt中，＝900，CD⊥AB，D为垂足，如果AB＝13，CD＝6，则AC＋BC等于：
A、17
B、5 C、13 D、9
22、已知一直角三角形的周长是
，斜边上的中线长是2，则这个三角形的面积是：
A、
5
B、
C、
D、1
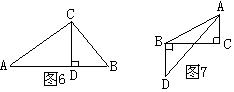
23、若CD是Rt的斜边AB上的高，且AB＝25，BC＝20，则DB和CD的长分别为：
A、16和9 B、9和16 C、16和12 D、12和16
三、解答题
1、已知00＜＜1800，00＜θ＜1800，且
，
求
的值。
2、
中，＝900，c=17，内切圆半径r＝3，求两条直角边a、b。
3、如图7，AC⊥BC，DB⊥BC，AB＝BD＝5，AC＝3，求AD。
4、在中，
求：①c的长 ②sinA的值 ③求AB边上的高h
5、如图8，在中，已知
的平分线AD=12，求其余各边的长，各角的度数和的内切圆的半径的长。
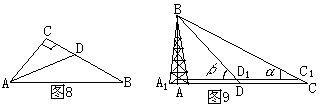
6、如图9，要测铁塔的高AB，从与铁塔底部在同一水平直线上的C、D两处，用测角仪器测得铁塔顶B的仰角分别为
，C、D间距离为14米，测角仪器的高为1米，求铁塔的高(不取近似值)
7、如图10，要测底部不能到达的塔AB的高，在地面上与塔底B同在一条直线上的C、D两点分别测得塔顶A的仰角为450和300，CD的距离为20米，求塔高(精确到0.1米)。
8、如图11，两建筑物的水平距离为36米，从A点测得D点的俯角
为360，测得C点的俯角为450，求这两个建筑物的高(精确到0.1米)(已知tg360=0.7265,ctg360=1.3764)。
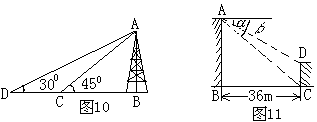
9、如图16，在中，
，AB＝6厘米，BC＝3厘米，点P从点A开始沿AB边向点B以1厘米/秒的速度移动，点Q从点B开始沿BC边向点C以2厘米/秒的速度移动，如果P、Q分别从A、B同时出发，几秒钟后P、Q间的距离等于
厘米？
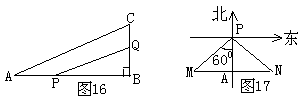
10、如图17，一只船自西向东航行，上午10时到一座灯塔P的南偏西600距塔68海里的M处，下午2时到达这座灯塔的南偏东600的N处，求这只船航行的速度(
，精确到0.1海里)。
11、海面上有A、B、C、O四条测量船，已知A在O的正南，B在O的正西，C在A的北偏东150，B在A的北偏西300，C在B的北偏东450，A、B相距10海里，求O与C的距离。
12、如图20，某海轮以30海里/时的速度航行，在A点测得海面上油井P在南偏东600，向北航行40分钟后到达B点，测得油井P在南偏东300，海轮改为东偏北300的航向再航行80分钟到达C点，试求P、C间的距离(计算结果保留根号)。
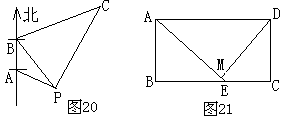
13、如图21，在矩形ABCD中，AB＝3，BC＝6，且BE＝2EC，DM⊥AE于M，求：sin
的值。
14、如图22，在中，CD是的平分线，，BC＝a，CA＝b，AB＝c，b＜x＜c是关于x的不等式x2-(m+1)x+3m+4＜0的解集，的面积为，求：①m的值
②a、b、c的值 ③CD的长
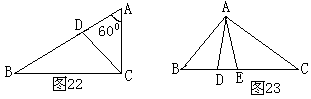
15、如图23，在Rt中，
，AE平分
，若AB=15，BD=9，求：①BC的长 ②AC的长
③AE的长
参考答案
一、填空题
1、 
2、3.6 3、 4、
5、300或1500
6、1 7、
8、45 9、
10、1200 11、6
12、
13、450 14、2＋ 15、－
16、1-sinA
18、10
19、
二、选择题
1、A 2、C 3、D 4、A 5、C 6、C 7、A
8、D 9、A 10、D 11、B 12、B 13、C 14、D
15、B 16、D 17、B 18、B 19、C 20、A 21、B
22、B 23、C
三、解答题
1、±1 2、8,15 3、
4、①
②
③
5、
6、
米 7、27.3米 8、36米，9.9米
9、
秒 10、29.4海里/时
11、
海里 12、
海里 13、
14、①m=12
②7,5,8 ③
15、①25 ②20
③