九年级数学综合试题（五）

九年级数学综合试题（五）　

一、选择题：（下列各小题都给出了四个选项，其中只有一项符合题目要求，请将符合要求的选项字母代号填写在下面的答题栏内. 本大题共10小题，每小题4分，共计40分）

1．如果某物体的三视图是如图所示的三个图形，那么该物体的形状是

A．正方体　B．长方体　C．三棱柱　　D．圆锥

2．二次函数的顶点为

A．（3，-1）B．（3，1）C．（-3，1）D．（-3，-1）　　　 第4题

3．方程x(x+3)=x+3的解是

A．x=1　 B．x₁=0, x₂=-3　　C． x₁=1, x₂=3　  D． x₁=1, x₂=-3

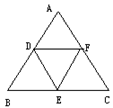
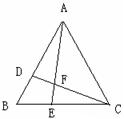
4．如图，D、E、F分别为△ABC三边的中点，则与△DEF全等的三角形有

A． 1个　B．　2个　 C．　3个　 D．　5个

5．已知反比例汉数经过点（-2，3），则这个反比例函数的表达式是

A．　　B．　　 C．　　D．

6．在中，，AB=15，sinA=，则BC等于

A．45　　B．5　　C．　　D．

7．下列图形中，既是轴对称图形又是中心对称图形的是

　　　　　

8．在下面图形中，每个大正方形网格都是由边长为1的小正方形组成，则图中阴影部分面积最大的是

　 　 　 

　　A．　　　　　  B．　　　　　　C．　　　　  D．

9．两道单选题都含有A、B、C、D四个选择支，瞎猜这两道题恰好全部猜对的概率有

A．　　B．　　 C．　　 D．

10．有一张矩形纸片ABCD，AB＝2.5，AD＝1.5，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AC与BC交于点F（如下图），则CF的长为

A．0.5　　B．0.75　　C．1　　D．1.25

二、填空题(本大题共6小题，每题5分，共30分)

11．分解因式:2x³－8x=_______．

12．某校九年级(1)班有50名同学, 综合数值评价”运动与健康”方面的等级统计如图所示, 则该班”运动与健康”评价等级为A的人数是______．

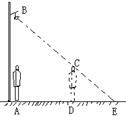
13．如图，小明从路灯下，向前走了5米，发现自己在地面上的影子长DE是2米，如果小明的身高为1.6米，那么路灯离地面的高度AB是_________米．

第12题　　　　　　　  第13题　　　　　　　 第16题

14．在四边形ABCD中，给出下列条件：①AB∥CD，②AD=BC，③∠B=∠D，以其中两个作为题设，另一个作结论，用“如果……，那么……．”的形式，写出一个真命题是　　　 ．

15．已知一列数：1，―2，3，―4，5，―6，7，…　将这列数排成下列形式：

第1行　　1

第2行　 －2　　　 3

第3行　 －4　　　 5　　　－6

第4行　　 7　　　－8　　 　9　　　－10

第5行　　 11　　－12　　　 13　　 －14　　 15

…　　　　 …

按照上述规律排下去，那么第10行从左边数第5个数等于　　　 ．

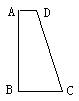
16．如图，已知直角梯形ABCD中，AD∥BC， AB⊥BC， AD=2、BC=3、AB=7，E是AB边上的一点，若以A、D、E为顶点的三角形和以E、B、C为顶点的三角形相似，则AE的长为________．

三、解答题（本题有8小题，第17题12分，18～20题每题8分，第21题９分，第22题9分，23题每题12分，第24题14分，共80分）

17．（本小题满分12分）

（1）请将下面的代数式尽可能化简, 再选择一个你喜欢的数(要合适哦!)代入求值：

（1+）÷． （6分）

（2）计算：°．（6分）

18．（本小题满分8分）) 如图，在△ABC中，点D在AB上，点E在BC上，BD＝BE。

(1)请你再添加一个条件，使得△BEA≌△BDC，并给出证明．

你添加的条件是：___________．（共6分）

(2)．根据你添加的条件，再写出图中的一对全等三角形：__________（只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）．（2分）

19．（本小题满分8分）下图为住宅区内的两幢楼，它们的高，现需了解甲楼对乙楼的采光的影响情况。当太阳光与水平线的夹角为30°时。试求：

（1）若两楼间的距离时，甲楼的影子，落在乙楼上有多高？（4分）

（2）若甲楼的影子，刚好不影响乙楼，那么两楼的距离应当有多远？（4分）

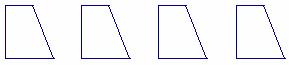
20．（本小题满分8分）请将四个全等直角梯形(如图)，拼成一个平行四边形，并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法)．

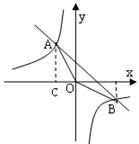21．（本小题满分9分）已知反比例函数与一次函数y=-x+m+10的图象交于A、B两点，过A作AC⊥x轴于C，且=4，

求：（1）反比例函数和一次函数的表达式．（3分）

(２)A、B两点的坐标；（3分）

(３)△AOB的面积．（3分）

22．（本小题满分9分）课改实验区学生的综合素质状况受到全社会的广泛关注。义乌市有关部门对全市9200名学生数学学业考试状况进行了一次抽样调查，从中随机抽查了5所初中九年级全体学生的数学调考成绩，右图是2005年5月抽样情况统计图．这5所初中的九年级学生的得分情况如下表（数学学业模拟考试满分120分）．

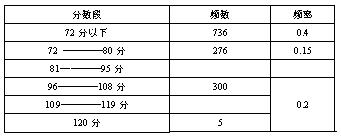
（1）这5所初中九年级学生的总人数有多少人？（2分）

（2）统计时,老师漏填了表中空白处的数据，请你帮老师填上．（3分）

(3)随机抽取一人，恰好是获得120分的概率是多少？（2分）

(4)从上表中，你还能获得其它的信息吗?（写出一条即可）．（2分）

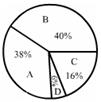
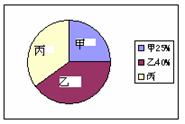
23．（本小题满分12分）快乐公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如右表所示．

	甲	乙	丙
优品率	80%	85%	90%

⑴求快乐公司从丙厂应购买多少件产品Ａ；（3分）

⑵求快乐公司所购买的200件产品A的优品率；（3分）

⑶你认为快乐公司能否通过调整从三个工厂所购买的产品A的比例，使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．（6分）

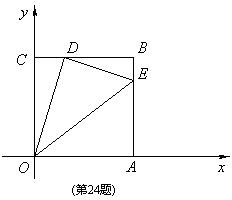24．（本小题满分14分）如图，边长为1的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动(不与B，C重合)，连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．记CD的长为t．

(1) 当t＝时，求直线DE的函数表达式；（4分）

(2) 如果记梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由；（5分）

(3) 当OD²＋DE ²的算术平方根取最小值时，

求点E的坐标．（5分）