中考数学学科练习题
(满分150分 考试时间100分钟)
2007年4月
| 题号 | 一 | 二 | 三 | 四 | 总分 | |||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| |||
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
|
考生注意:
1、本卷含四大题,共25题。
2、除第一、二大题外,其余各题如无特别说明,都必须写出证明或计算的主要步骤。
| 得分 | 评卷 |
|
|
|
一、填空题(本大题共12题,每题3分,满分36分)
【只要求直接写出结果,每个空格填对得3分,否则得零分】
1、化简:![]() =__________.
=__________.
2、计算:![]() =__________.
=__________.
3、点![]() 关于
关于![]() 轴对称的点的坐标是__________.
轴对称的点的坐标是__________.
4、函数![]() 中,自变量x的取值范围是__________.
中,自变量x的取值范围是__________.
5、设![]() 、
、![]() 是方程
是方程![]() 的两个实数根,则
的两个实数根,则![]() __________.
__________.
6、不等式组![]() 的解集是__________.
的解集是__________.
7、方程![]() 的根是__________.
的根是__________.
8、抛物线![]() 的对称轴是直线__________.
的对称轴是直线__________.
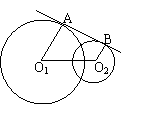
|
|
|
|
|
| |||||||||||||
| |||||||||||||
 | |||||||||||||
 | |||||||||||||
| |||||||||||||
| |||||||||||||
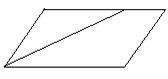
10、如图,平行四边形ABCD中,![]() 的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是____________.
的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是____________.
11、如图,若⊙![]() 的半径为10,⊙
的半径为10,⊙![]() 的半径为5,圆心距是13,则两圆的外公切线AB长是__________.
的半径为5,圆心距是13,则两圆的外公切线AB长是__________.
![]()
![]()
![]()
|
|
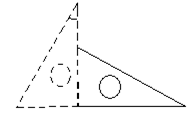 12、如图,斜边长12cm,
12、如图,斜边长12cm,左平移使点B′落在原三角尺ABC的斜边AB上,则三角尺向左平移的距离为__________cm.(结果保留根号)
![]()
| |||
| 得分 | 评卷 |
|
|
|
![]() 二、选择题:(本大题共4题,每题4分,满分16分)
二、选择题:(本大题共4题,每题4分,满分16分)
【下列各题的四个结论中,有且只有一个结论是正确的,把正确结论的代号写在题后的圆括号内,选对得4分;不选、错选或者多选得零分】
13、下列运算中,正确的是………………………………………………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14、如果关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围是…( )
的取值范围是…( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
|
|
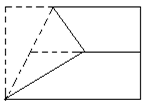 A.正多边形一定是中心对称图形
A.正多边形一定是中心对称图形
|
|
|
D.三角形的重心到顶点的距离是它到对边距离的2倍
![]()
|
|
AECD的中位线FG上,若![]() ,则AE的长为……
,则AE的长为……
………………………………………………………………………………………( )
A. ![]() B.
6
C. 3
D. 4
B.
6
C. 3
D. 4
| 得分 | 评卷 |
|
|
|
三、(本大题共5题,满分48分)
17、(本题满分9分)
先化简,再求值:![]() ,其中
,其中![]() .
.
| 得分 | 评卷 |
|
|
|
18、(本题满分9分)
解方程组:![]()
| 得分 | 评卷 |
|
|
|
|
|
|
|
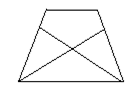
求证:AF=BE
 |
| 得分 | 评卷 |
|
|
|
20、(本题满分10分)
|
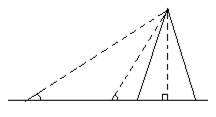 小杨同学为了测量一铁塔的高度CD,如图,他先在A处测得塔顶C的仰角为
小杨同学为了测量一铁塔的高度CD,如图,他先在A处测得塔顶C的仰角为
 |
| 得分 | 评卷 |
|
|
|
21、(本题满分10分)
为了解某区九年级学生的身高情况,从中随机抽取250名学生的身高作为一个样本,身高均在151~185cm之间(取整厘米),整理后分成7组,绘制出频数分布直方图(不完整),根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图,并标出学生数。
(2)抽取的样本中,学生身高的中位数在哪个小组?(写出身高范围)
(3)该区共有4000名九年级学生,估计其中身高不低于171cm的人数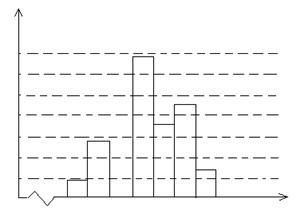 .
.
 | |||||||
| |||||||
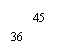 | |||||||
| |||||||
|
|
四、(本大题共4题,满分50分)
| 得分 | 评卷 |
|
|
|
22、(本题满分12分)
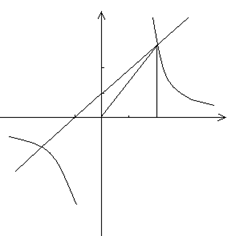 如图,已知反比例函数
如图,已知反比例函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,过点
,过点![]() 作
作
![]()
|
(1)求![]() 与
与![]() 的值.
的值.
|
![]()
![]()
|
和![]() 的值.
的值.
|
| 得分 | 评卷 |
|
|
|
23、(本题满分12分)
某公司![]() 名员工准备外出旅游,有两项支出需提前预算:
名员工准备外出旅游,有两项支出需提前预算:
(1)备用食品费:购买备用食品共花费510元,在出发前时,又有2名员工要加入(不再增加备用食品费),因此,先参加的员工平均每人比原来少分摊4元,现在每人需分摊多少元食品费?
(2)租车费:现在有两种车型可供租用,座数和租车费如下表所示:
| 车型 | 座数 | 租车费(元/辆) |
| A | 7 | 500 |
| B | 10 | 600 |
请选择最合算的租车方案(仅从租车费角度考虑),并说明理由.
| 得分 | 评卷 |
|
|
|
24、(本题满分12分)
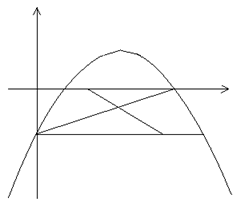
如图,二次函数![]() 的图象与
的图象与![]() 轴相交于点A、B,与
轴相交于点A、B,与![]() 轴
轴
相交于点C,连结AC.
(1)求证:![]() ∽
∽![]() .
.
(2)过点C作CD//![]() 轴交二次函数
轴交二次函数![]() 的图象于点D,若点M在线段AB上以每秒1个单位的速度由A向B运动,同时点N在线段CD上也以每秒1个单位的速度由点D向点C运动,连结线段MN,设运动时间为t秒.(
的图象于点D,若点M在线段AB上以每秒1个单位的速度由A向B运动,同时点N在线段CD上也以每秒1个单位的速度由点D向点C运动,连结线段MN,设运动时间为t秒.(![]() )
)
① 是否存在时刻t,使MN=AC?若存在,求出t的值;若不存在,请说明理由.
② 是否存在时刻t,使MN![]() BC?若存在,直接写出t的值;若不存在,请说明理由.
BC?若存在,直接写出t的值;若不存在,请说明理由.
|
![]()
![]()
![]()
![]()
| ||||
![]()
![]()
![]()
|
| 得分 | 评卷 |
|
|
|
25、(本题满分14分)
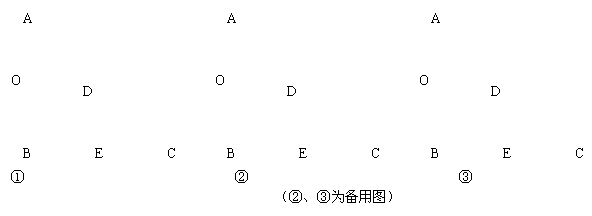
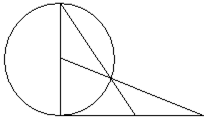
如图①,已知AB是⊙![]() 的直径,BC是⊙
的直径,BC是⊙![]() 的切线,OC与⊙
的切线,OC与⊙![]() 相交于点D,连结AD并延长交BC于点E,BC=3,CD=2
相交于点D,连结AD并延长交BC于点E,BC=3,CD=2
(1)求⊙![]() 的半径.
的半径.
(2)取BE的中点F,连结DF,求证:DF是⊙![]() 的切线.
的切线.
(3)过点D作DG![]() BC,垂足为G,OE与DG相交于点M,连结BM并延长,与OC相交于点N,试确定以N为圆心,经过点E的⊙
BC,垂足为G,OE与DG相交于点M,连结BM并延长,与OC相交于点N,试确定以N为圆心,经过点E的⊙![]() 与⊙
与⊙![]() 的位置关系(说明理由),并求出⊙
的位置关系(说明理由),并求出⊙![]() 的半径.
的半径.
 |


2007年虹口区数学学科中考练习题
参考答案与评分意见 2007.4.
一、填空题(本大题共12题,每题3分,满分36分)
【只要求直接写出结果,每个空格填对得3分,否则得零分】
1、![]() ;2、
;2、![]() ;3、(1,2);4、
;3、(1,2);4、![]() ;5、1;6、
;5、1;6、![]() ;7、
;7、![]() ;8、
;8、![]() ;9、2;10、14;11、12;12、
;9、2;10、14;11、12;12、![]()
二、选择题:(本大题共4题,每题4分,满分16分)
【下列各题的四个结论中,有且只有一个结论是正确的,把正确结论的代号写在题后的圆括号内,选对得4分;不选、错选或者多选得零分】
13、B;14、A;15、C;16、D
三、(本大题共5题,满分48分)
17、解:原式=![]() ………………………………………………………………(4分)
………………………………………………………………(4分)
=![]() …………………………………………………………………(1分)
…………………………………………………………………(1分)
=![]() ………………………………………………………………………(2分)
………………………………………………………………………(2分)
|
18、解:
![]()
①×2得:![]() ③…………………………………………………(2分)
③…………………………………………………(2分)
②×3得:![]() ④…………………………………………………(2分)
④…………………………………………………(2分)
④-③得:![]() ……………………………………………………………(2分)
……………………………………………………………(2分)
![]() ……………………………………………………………(1分)
……………………………………………………………(1分)
把![]() 代入①得:
代入①得:![]()
![]() ………………………………………………(1分)
………………………………………………(1分)
![]() 原方程组的解是
原方程组的解是![]() ……………………………………………………(1分)
……………………………………………………(1分)
19、证明:∵四边形ABCD是等腰梯形
![]() ∠DAB=∠CBA,AD=BC………………………………………………………(2分)
∠DAB=∠CBA,AD=BC………………………………………………………(2分)
又∵DE=CF
![]() AE=BF………………………………………………………………………(2分)
AE=BF………………………………………………………………………(2分)
在△AFB与△BEA中,
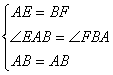 …………………………………………………………(3分)
…………………………………………………………(3分)
![]() △AFB≌△BEA……………………………………………………………(2分)
△AFB≌△BEA……………………………………………………………(2分)
![]() AF=BE……………………………………………………………………(1分)
AF=BE……………………………………………………………………(1分)
20、解:在Rt△ADC中,AD=DC![]() …………………………………………………(2分)
…………………………………………………(2分)
在Rt△BDC中,BD=DC![]() …………………………………………………(2分)
…………………………………………………(2分)
∵AD-BD=AB=40…………………………………………………………………(2分)
![]() DC(
DC(![]() )=40…………………………………………………(1分)
)=40…………………………………………………(1分)
![]() DC=
DC=![]() =
=![]() (米)………………………………(2分)
(米)………………………………(2分)
答:这座铁塔的高度约为34.6米。……………………………………………(1分)
21、解:(1)补全频数分布直方图略。160.5~165.5学生数50人……………(2分,1分)
(2)中位数在165.5~170.5cm小组内…………………………………………(3分)
(3)样本中身高不低于171cm的人数为36+45+14=95(人)………………(2分)
在样本中所占的比例为![]() ,
,
所以该区身高不低于171cm的九年级学生人数估计有:
![]() (人)……………………………………(2分)
(人)……………………………………(2分)
四、(本大题共4题,满分50分)
22、解:(1)∵A(2,m)在第一象限
![]() m>0,
m>0, ![]() OB=2,AB=m………………………………………………………(1分)
OB=2,AB=m………………………………………………………(1分)
∵![]() OB•AB=
OB•AB=![]()
![]() ………………………………………………………………………(2分)
………………………………………………………………………(2分)
![]() A(2,3)
A(2,3)
把A(2,3)代入![]() 中,得:
中,得:![]() ,
,![]() …………………………(2分)
…………………………(2分)
(2)把A(2,3)代入![]() 中,得:
中,得:
![]()
![]()
![]() …………………………………………………(1分)
…………………………………………………(1分)
令![]() ,得:
,得:![]()
![]()
![]() 点C的坐标为(-1,0)………………………………(1分)
点C的坐标为(-1,0)………………………………(1分)
![]() CB=2-(-1)=3,又AB=3,AB
CB=2-(-1)=3,又AB=3,AB![]() 轴
轴
![]() ∠ACB=
∠ACB=![]() ………………………………………………(2分)
………………………………………………(2分)
![]()
![]() ………………(1分)
………………(1分)
又Rt△AOB中,![]() …………………(1分)
…………………(1分)
![]() ……………………………………(1分)
……………………………………(1分)
23、解:(1)设现在每人需分摊![]() 元食品费,则原来每人需分摊(
元食品费,则原来每人需分摊(![]() )元食品费,根据题意,得:……………………………………………………………………(1分)
)元食品费,根据题意,得:……………………………………………………………………(1分)
![]() …………………………………………………(3分)
…………………………………………………(3分)
去分母,整理,得:![]()
解得:![]() …………………………………………………(1分)
…………………………………………………(1分)
经检验,![]() 都是原方程的根,但
都是原方程的根,但![]() 不合题意,舍去,所以
不合题意,舍去,所以![]() …………………………………………………………………(1分)
…………………………………………………………………(1分)
答:现在每人需分摊30元食品费。………………………………………(1分)
(2)由(1)可计算旅游人数是:
510÷30=17(人)…………………………………………(1分)
方案1:租3辆A型车,费用是:
500×3=1500(元)…………………………………………(1分)
方案2:租2辆B型车,费用是:
600×2=1200(元)…………………………………………(1分)
方案3:租1辆A型车,租1辆B型车,费用是:
500+600=1100(元)………………………………………(1分)
所以,选择方案3最合算。…………………………………………………(1分)
24、解:(1)令![]() ,得:
,得:![]()
解得:![]()
令![]() ,得:
,得:![]()
![]() …………………………………………………(2分)
…………………………………………………(2分)
![]()
![]() ………………………………………………………………(1分)
………………………………………………………………(1分)
又∵∠AOC=∠COB…………………………………………………………(1分)
![]() ∽
∽![]()
(2)① 存在,t=5或3…………………………………………………………(1分)
解法1: 由题意,得:AM=DN=t………………………………………………………(1分)
∵A(2,0),B(8,0) ![]() AB=8-2=6
AB=8-2=6
![]() MB=6-t………………………………………………………………………(1分)
MB=6-t………………………………………………………………………(1分)
∵CD//![]() 轴,点C(0,-4)
轴,点C(0,-4)
![]() 点D的纵坐标为-4
点D的纵坐标为-4
∵点D在二次函数![]() 的图象上
的图象上
![]()
![]()
![]()
![]()
![]()
![]() ……………………………………………………(1分)
……………………………………………………(1分)
Ⅰ 当AM=CN,即四边形ACNM是平行四边形时,MN=AC,
此时,t=10-t,![]() …………………………………………………………(1分)
…………………………………………………………(1分)
Ⅱ 连接BD,当MB=DN,即四边形MNDB是平行四边形时,
可证: MN=BD=AC
此时, 6-t=t
![]() …………………………………………(1分)
…………………………………………(1分)
所以,当t=5或3时,MN=AC
解法2:t秒后,可得:![]() ,
,![]() ,
,![]() ,
,![]() …………(2分)
…………(2分)
∴![]() …………………………………………………(2分)
…………………………………………………(2分)
∴由题意,得:![]() ……………………………………………………(1分)
……………………………………………………(1分)
解得:![]()
② 存在,t=3……………………………………………………………………………(2分)
25.解:(1)∵AB是⊙![]() 的直径,BC是⊙
的直径,BC是⊙![]() 的切线
的切线
![]() ,…………………………………………………………………(1分)
,…………………………………………………………………(1分)
设⊙![]() 的半径为r,在Rt
的半径为r,在Rt![]() 中,
中,![]() =
=![]()
![]() …………………………………………………………(1分)
…………………………………………………………(1分)
解得:r=![]() ……………………………………………………………………(1分)
……………………………………………………………………(1分)
![]() ⊙
⊙![]()
![]()
|
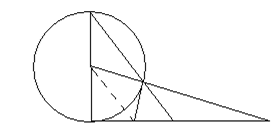 (2)如图②,连接OF.
(2)如图②,连接OF.
|
|
|
|
|
|
|
|
|
又∵![]()
![]() ≌
≌![]() ……………………………………………………………(1分)
……………………………………………………………(1分)
![]() 即
即![]() …………………………………(1分)
…………………………………(1分)
∵
|
![]()
![]() 是⊙
是⊙![]() 的切线。
的切线。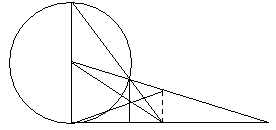
(3) ⊙![]() 与⊙
与⊙![]() 外切………………………(1分)
外切………………………(1分)
|
|
|
|
|
|
|
|
|
![]()
![]() ,
, ![]() ……………………………………………(1分)
……………………………………………(1分)
又∵![]()
![]()
![]() ……………………………………………(1分)
……………………………………………(1分)
![]() 又
又![]()
![]()
![]()
∵![]() …………………………………………………(1分)
…………………………………………………(1分)
![]() 圆心距ON等于⊙
圆心距ON等于⊙![]() 的半径与⊙
的半径与⊙![]() 的半径的和…………………………(1分)
的半径的和…………………………(1分)
![]() ⊙
⊙![]() 与⊙
与⊙![]() 外切。
外切。
设⊙![]() 的半径为x
的半径为x
∵![]()
![]() ,
, 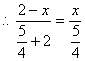 ……………………………………………(1分)
……………………………………………(1分)
![]() ………………………………………………………………………(1分)
………………………………………………………………………(1分)
![]() ⊙
⊙![]() 的半径为
的半径为![]()
|